Informal Essay By English
In the difficult employment situation, we need to set a good goal and then do our own thing

参考书籍:“凤凰架构”
进程缓存(Cache)
缓存在分布式系统是可选,在使用缓存之前需要确认你的系统是否真的需要缓存,因为从开发角度来说,引入缓存会提高系统复杂度,因为你要考虑缓存的失效、更新、一致性等问题(硬件缓存也有这些问题,只是不需要由你去考虑,主流的 ISA 也都没有提供任何直接操作缓存的指令);从运维角度来说,缓存会掩盖掉一些缺陷,让问题在更久的时间以后,出现在距离发生现场更远的位置上;从安全角度来说,缓存可能泄漏某些保密数据,也是容易受到攻击的薄弱点。如果上诉的几种引入缓存所带来的困难你都可以接受,那就说明目前你的系统目前碰到的问题所带来的影响远远比上诉的几种困难更加难以接受,而引入缓存的理由,总结起来无外乎以下两种:
- 为缓解 CPU 压力而做缓存:譬如把方法运行结果存储起来、把原本要实时计算的内容提前算好、把一些公用的数据进行复用,这可以节省 CPU 算力,顺带提升响应性能。
- 为缓解 I/O 压力而做缓存:譬如把原本对网络、磁盘等较慢介质的读写访问变为对内存等较快介质的访问,将原本对单点部件(如数据库)的读写访问变为到可扩缩部件(如缓存中间件)的访问,顺带提升响应性能。
而最常见的一种也是使用较多的进程中的内存缓存之一就是jdk提供的HashMap,虽然HashMap拥有缓存数据的能力,但是功能比较单一,并且这个HashMap缓存容器的操作并不是一个并发安全的容器。虽然jdk提供了Collections.synchronizedMap()工具类去获取并发安全容器,这在一定程度上解决了并发安全的问题,但是由于Collections工具类创建的容器是通过在方法里面加synchronize的方法保证并发安全,这种细粒度的锁无法保证在高并发的情况的操作容器数据的一个高吞吐量(OPS)
//以下是使用Collections.synchronizedMap()方法创建容器的常见api,都是通过synchronized关键字保证的并发安全,但是无法保证高并发下的高吞吐量
public V get(Object key) {
synchronized (mutex) {return m.get(key);}
}
public V put(K key, V value) {
synchronized (mutex) {return m.put(key, value);}
}
public V remove(Object key) {
synchronized (mutex) {return m.remove(key);}
}
为了保证高并发下的高吞吐量,jdk提供了ConcurrentHashMap并发容器给开发人员使用,此容器相比较Collections工具类创建的容器最大的区别在于使用更细粒度的锁去保证高并发情况操作数据的安全(jdk1.7采用的是分段锁、jdk1.8则是采用cas+synchronize锁单个元素去保证并发安全),以此来提高吞吐量。
尽管jdk已经提供了基础缓存能力的一些容器给我们使用,但是也无法满足日益增长的业务场景需要,因此Caffeine、Guave等一系列进程内缓存实现方案相继出现,而开发人员如何抉择缓存方案则一般需要从以下四个维度去考量:
- 吞吐量:缓存的吞吐量使用 OPS 值(每秒操作数,Operations per Second,ops/s)来衡量,反映了对缓存进行并发读、写操作的效率,即缓存本身的工作效率高低
- 命中率:缓存的命中率即成功从缓存中返回结果次数与总请求次数的比值,反映了引入缓存的价值高低,命中率越低,引入缓存的收益越小,价值越低。
- 扩展功能:缓存除了基本读写功能外,还提供哪些额外的管理功能,譬如最大容量、失效时间、失效事件、命中率统计,等等。
- 分布式支持:缓存可分为“进程内缓存”和“分布式缓存”两大类,前者只为节点本身提供服务,无网络访问操作,速度快但缓存的数据不能在各个服务节点中共享,后者则相反
吞吐量
并发读写的场景中,吞吐量受多方面因素的共同影响,譬如,怎样设计数据结构以尽可能避免数据竞争,存在竞争风险时怎样处理同步(主要有使用锁实现的悲观同步和使用CAS实现的乐观同步)、如何避免伪共享现象(False Sharing,这也算是典型缓存提升开发复杂度的例子)发生,等等。其中第一点是格外重要的一点,无论如何实现同步都不会比直接无须同步更快。那么如果是我们自己去设计一个缓存容器,应该如何避免竞争、提高吞吐量呢?
缓存中最主要的数据竞争源于读取数据的同时,也会伴随着对数据状态的写入操作,写入数据的同时,也会伴随着数据状态的读取操作。譬如,读取时要同时更新数据的最近访问时间和访问计数器的状态(后文会提到,为了追求高效,可能不会记录时间和次数,譬如通过调整链表顺序来表达时间先后、通过 Sketch 结构来表达热度高低),以实现缓存的淘汰策略;又或者读取时要同时判断数据的超期时间等信息,以实现失效重加载等其他扩展功能。对以上伴随读写操作而来的状态维护,有两种可选择的处理思路,一种是以 Guava Cache 为代表的同步处理机制,即在访问数据时一并完成缓存淘汰、统计、失效等状态变更操作,通过分段加锁等优化手段来尽量减少竞争。另一种是以 Caffeine 为代表的异步日志提交机制,这种机制参考了经典的数据库设计理论,将对数据的读、写过程看作是日志(即对数据的操作指令)的提交过程。尽管日志也涉及到写入操作,有并发的数据变更就必然面临锁竞争,但异步提交的日志已经将原本在 Map 内的锁转移到日志的追加写操作上,日志里腾挪优化的余地就比在 Map 中要大得多。
在 Caffeine 的实现中,设有专门的环形缓存区(Ring Buffer,也常称作 Circular Buffer)来记录由于数据读取而产生的状态变动日志。为进一步减少竞争,Caffeine 给每条线程(对线程取 Hash,哈希值相同的使用同一个缓冲区)都设置一个专用的环形缓冲。
所谓环形缓冲,并非 Caffeine 的专有概念,它是一种拥有读、写两个指针的数据复用结构,在计算机科学中有非常广泛的应用。举个具体例子,譬如一台计算机通过键盘输入,并通过 CPU 读取“HELLO WIKIPEDIA”这个长 14 字节的单词,通常需要一个至少 14 字节以上的缓冲区才行。但如果是环形缓冲结构,读取和写入就应当一起进行,在读取指针之前的位置均可以重复使用,理想情况下,只要读取指针不落后于写入指针一整圈,这个缓冲区就可以持续工作下去,能容纳无限多个新字符。否则,就必须阻塞写入操作去等待读取清空缓冲区。
从 Caffeine 读取数据时,数据本身会在其内部的 ConcurrentHashMap 中直接返回,而数据的状态信息变更就存入环形缓冲中,由后台线程异步处理。如果异步处理的速度跟不上状态变更的速度,导致缓冲区满了,那此后接收的状态的变更信息就会直接被丢弃掉,直至缓冲区重新富余。通过环形缓冲和容忍有损失的状态变更,Caffeine 大幅降低了由于数据读取而导致的垃圾收集和锁竞争,因此 Caffeine 的读取性能几乎能与 ConcurrentHashMap 的读取性能相同。
向 Caffeine 写入数据时,将使用传统的有界队列(ArrayQueue)来存放状态变更信息,写入带来的状态变更是无损的,不允许丢失任何状态,这是考虑到许多状态的默认值必须通过写入操作来完成初始化,因此写入会有一定的性能损失。根据 Caffeine 官方给出的数据,相比ConcurrentHashMap,Caffeine 在写入时大约会慢 10%左右。
命中率与淘汰策略
命中率和淘汰策略放在一起说明是因为缓存的淘汰策略会直接影响缓存的命中效率,当然,如果你的缓存没有淘汰策略命中率肯定是最高的,但是有限的物理存储决定了任何缓存的容量都不可能是无限的,所以缓存需要在消耗空间与节约时间之间取得平衡,这要求缓存必须能够自动或者由人工淘汰掉缓存中的低价值数据。
而什么叫做“低价值”数据呢?由于缓存的通用性,这个问题的答案必须是与具体业务逻辑是无关的,只能从缓存工作过程收集到的统计结果来确定数据是否有价值,通用的统计结果包括但不限于数据何时进入缓存、被使用过多少次、最近什么时候被使用,等等。由此决定了一旦确定选择何种统计数据,及如何通用地、自动地判定缓存中每个数据价值高低,也相当于决定了缓存的淘汰策略是如何实现的。目前,最基础的淘汰策略实现方案有以下三种:
FIFO(First In First Out):优先淘汰最早进入被缓存的数据。FIFO 实现十分简单,但一般来说它并不是优秀的淘汰策略,越是频繁被用到的数据,往往会越早被存入缓存之中。如果采用这种淘汰策略,很可能会大幅降低缓存的命中率。(此缓存相比较简单,因此)
LRU(Least Recent Used):优先淘汰最久未被使用访问过的数据。LRU 通常会采用 HashMap 加 LinkedList 双重结构(如 LinkedHashMap)来实现,以 HashMap 来提供访问接口,保证常量时间复杂度的读取性能,以 LinkedList 的链表元素顺序来表示数据的时间顺序,每次缓存命中时把返回对象调整到 LinkedList 开头,每次缓存淘汰时从链表末端开始清理数据。对大多数的缓存场景来说,LRU 都明显要比 FIFO 策略合理,尤其适合用来处理短时间内频繁访问的热点对象。但相反,它的问题是如果一些热点数据在系统中经常被频繁访问,但最近一段时间因为某种原因未被访问过,此时这些热点数据依然要面临淘汰的命运,LRU 依然可能错误淘汰价值更高的数据。案例如下:
/**
* LRUCache implementation
*
* @author disaster
* @version 1.0
*
* @param <K>
* @param <V>
*/
public class LRUCache<K, V> extends LinkedHashMap<K, V> {
public static final LRUCache<String,ReentrantLock> LOCK_CACHE_INSTANCE = new LRUCache<String,ReentrantLock>(10000);
private static final long serialVersionUID = -5167631809472116969L;
private static final float DEFAULT_LOAD_FACTOR = 0.75f;
private static final int DEFAULT_MAX_CAPACITY = 1000;
private final Lock lock = new ReentrantLock();
private volatile int maxCapacity;
public LRUCache() {
this(DEFAULT_MAX_CAPACITY);
}
public LRUCache(int maxCapacity) {
super(16, DEFAULT_LOAD_FACTOR, true);
this.maxCapacity = maxCapacity;
}
@Override
protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) {
return size() > maxCapacity;
}
@Override
public boolean containsKey(Object key) {
try {
lock.lock();
return super.containsKey(key);
} finally {
lock.unlock();
}
}
@Override
public V get(Object key) {
try {
lock.lock();
return super.get(key);
} finally {
lock.unlock();
}
}
@Override
public V put(K key, V value) {
try {
lock.lock();
return super.put(key, value);
} finally {
lock.unlock();
}
}
@Override
public V remove(Object key) {
try {
lock.lock();
return super.remove(key);
} finally {
lock.unlock();
}
}
@Override
public int size() {
try {
lock.lock();
return super.size();
} finally {
lock.unlock();
}
}
@Override
public void clear() {
try {
lock.lock();
super.clear();
} finally {
lock.unlock();
}
}
public int getMaxCapacity() {
return maxCapacity;
}
public void setMaxCapacity(int maxCapacity) {
this.maxCapacity = maxCapacity;
}
}
/**
* 哈希链表实现LRU
*
* @author disaster
* @version 1.0
* @param <K>
* @param <V>
*/
public class ILRUCache<K, V> {
private HashMap<K, Node<K, V>> map;
private BidirectionalLinkedList<K, V> cache;
// 最大容量
private int cap;
public ILRUCache(int cap) {
this.cap = cap;
this.map = new HashMap<K, Node<K, V>>();
this.cache = new BidirectionalLinkedList<K, V>();
}
public void put(K key, V value) {
if (map.containsKey(key)) {
remove(key);
addRecently(key, value);
return;
}
if (map.size() == cap) {
removeLeastRecently();
}
addRecently(key, value);
}
public V get(K key) {
if (!map.containsKey(key)) {
return null;
}
makeRecently(key);
return map.get(key).getValue();
}
public void makeRecently(K key) {
Node<K, V> kvNode = map.get(key);
cache.remove(kvNode);
cache.addLast(kvNode);
}
public void removeLeastRecently() {
Node<K, V> kvNode = cache.removeFirst();
// 同时别忘了从 map 中删除它的 key
assert kvNode != null;
K deletedKey = kvNode.key;
map.remove(deletedKey);
}
public void remove(K key) {
Node<K, V> x = map.get(key);
cache.remove(x);
map.remove(key);
cap--;
}
public void addRecently(K key, V value) {
Node<K, V> kvNode = new Node<>(key, value);
cache.addLast(kvNode);
map.put(key, kvNode);
cap++;
}
private static class BidirectionalLinkedList<K, V> {
private Node<K, V> head, tail;
private int size;
public BidirectionalLinkedList() {
this.head = new Node<K, V>((K) new Object(), (V) new Object());
this.tail = new Node<K, V>((K) new Object(), (V) new Object());
this.size = 0;
}
public void addLast(Node<K, V> x) {
x.prev = tail.prev;
x.next = tail;
tail.prev.next = x;
tail.prev = x;
size++;
}
// 删除链表中的 x 节点(x 一定存在)
// 由于是双链表且给的是目标 Node 节点,时间 O(1)
public void remove(Node<K, V> x) {
x.prev = x.next;
x.next.prev = x.prev;
size--;
}
// 删除链表中第一个节点,并返回该节点,时间 O(1)
public Node<K, V> removeFirst() {
if (head.next == tail) {
return null;
}
Node<K, V> first = head.next;
remove(first);
return first;
}
public int size() {
return size;
}
}
private static class Node<K, V> {
private K key;
private V value;
private Node<K, V> prev;
private Node<K, V> next;
public Node(K key, V value) {
this.key = key;
this.value = value;
}
public K getKey() {
return key;
}
public void setKey(K key) {
this.key = key;
}
public V getValue() {
return value;
}
public void setValue(V value) {
this.value = value;
}
public Node<K, V> getPrev() {
return prev;
}
public void setPrev(Node<K, V> prev) {
this.prev = prev;
}
public Node<K, V> getNext() {
return next;
}
public void setNext(Node<K, V> next) {
this.next = next;
}
}
}
LFU(Least Frequently Used):优先淘汰最不经常使用的数据。LFU 会给每个数据添加一个访问计数器,每访问一次就加 1,需要淘汰时就清理计数器数值最小的那批数据。LFU 可以解决上面 LRU 中热点数据间隔一段时间不访问就被淘汰的问题,但同时它又引入了两个新的问题,首先是需要对每个缓存的数据专门去维护一个计数器,每次访问都要更新,在上一节“吞吐量”里解释了这样做会带来高昂的维护开销;另一个问题是不便于处理随时间变化的热度变化,譬如某个曾经频繁访问的数据现在不需要了,它也很难自动被清理出缓存。案例:
/**
* LFU implementation
*
* @author wangwei
* @version 1.0
* @param <K>
* @param <V>
*/
public class LFUCache<K, V> {
public final static LFUCache<String,Object> CONDITIONS_RESULT_CACHE = new LFUCache<String,Object>(10000,0.75f);
public final static LFUCache<String,ReentrantLock> LOCK_CACHE_INSTANCE = new LFUCache<String,ReentrantLock>(10000,0.75f);
public final static String PREFIX = "LFU_PREFIX";
private Map<K, CacheNode<K, V>> map;
private CacheDeque<K, V>[] freqTable;
private final int capacity;
private int evictionCount;
private int curSize = 0;
private final ReentrantLock lock = new ReentrantLock();
private static final int DEFAULT_INITIAL_CAPACITY = 1000;
private static final float DEFAULT_EVICTION_FACTOR = 0.75f;
public LFUCache() {
this(DEFAULT_INITIAL_CAPACITY, DEFAULT_EVICTION_FACTOR);
}
/**
* Constructs and initializes cache with specified capacity and eviction
* factor. Unacceptable parameter values followed with
* {@link IllegalArgumentException}.
*
* @param maxCapacity cache max capacity
* @param evictionFactor cache proceedEviction factor
*/
@SuppressWarnings("unchecked")
public LFUCache(final int maxCapacity, final float evictionFactor) {
if (maxCapacity <= 0) {
throw new IllegalArgumentException("Illegal initial capacity: " +
maxCapacity);
}
boolean factorInRange = evictionFactor <= 1 && evictionFactor > 0;
if (!factorInRange) {
throw new IllegalArgumentException("Illegal eviction factor value:"
+ evictionFactor);
}
this.capacity = maxCapacity;
this.evictionCount = (int) (capacity * evictionFactor);
this.map = new HashMap<K, CacheNode<K, V>>();
this.freqTable = new CacheDeque[capacity + 1];
for (int i = 0; i <= capacity; i++) {
freqTable[i] = new CacheDeque<K, V>();
}
for (int i = 0; i < capacity; i++) {
freqTable[i].nextDeque = freqTable[i + 1];
}
freqTable[capacity].nextDeque = freqTable[capacity];
}
public int getCapacity() {
return capacity;
}
public V put(final K key, final V value) {
CacheNode<K, V> node;
lock.lock();
try {
node = map.get(key);
if (node != null) {
CacheNode.withdrawNode(node);
node.value = value;
freqTable[0].addLastNode(node);
map.put(key, node);
} else {
node = freqTable[0].addLast(key, value);
map.put(key, node);
curSize++;
if (curSize > capacity) {
proceedEviction();
}
}
} finally {
lock.unlock();
}
return node.value;
}
public V remove(final K key) {
CacheNode<K, V> node = null;
lock.lock();
try {
if (map.containsKey(key)) {
node = map.remove(key);
if (node != null) {
CacheNode.withdrawNode(node);
}
curSize--;
}
} finally {
lock.unlock();
}
return (node != null) ? node.value : null;
}
public V get(final K key) {
CacheNode<K, V> node = null;
lock.lock();
try {
if (map.containsKey(key)) {
node = map.get(key);
CacheNode.withdrawNode(node);
node.owner.nextDeque.addLastNode(node);
}
} finally {
lock.unlock();
}
return (node != null) ? node.value : null;
}
/**
* Evicts less frequently used elements corresponding to eviction factor,
* specified at instantiation step.
*
* @return number of evicted elements
*/
private int proceedEviction() {
int targetSize = capacity - evictionCount;
int evictedElements = 0;
FREQ_TABLE_ITER_LOOP:
for (int i = 0; i <= capacity; i++) {
CacheNode<K, V> node;
while (!freqTable[i].isEmpty()) {
node = freqTable[i].pollFirst();
remove(node.key);
if (targetSize >= curSize) {
break FREQ_TABLE_ITER_LOOP;
}
evictedElements++;
}
}
return evictedElements;
}
/**
* Returns cache current size.
*
* @return cache size
*/
public int getSize() {
return curSize;
}
static class CacheNode<K, V> {
CacheNode<K, V> prev;
CacheNode<K, V> next;
K key;
V value;
CacheDeque<K, V> owner;
CacheNode() {
}
CacheNode(final K key, final V value) {
this.key = key;
this.value = value;
}
/**
* This method takes specified node and reattaches it neighbors nodes
* links to each other, so specified node will no longer tied with them.
* Returns united node, returns null if argument is null.
*
* @param node note to retrieve
* @param <K> key
* @param <V> value
* @return retrieved node
*/
static <K, V> CacheNode<K, V> withdrawNode(
final CacheNode<K, V> node) {
if (node != null && node.prev != null) {
node.prev.next = node.next;
if (node.next != null) {
node.next.prev = node.prev;
}
}
return node;
}
}
/**
* Custom deque implementation of LIFO type. Allows to place element at top
* of deque and poll very last added elements. An arbitrary node from the
* deque can be removed with {@link CacheNode#withdrawNode(CacheNode)}
* method.
*
* @param <K> key
* @param <V> value
*/
static class CacheDeque<K, V> {
CacheNode<K, V> last;
CacheNode<K, V> first;
CacheDeque<K, V> nextDeque;
/**
* Constructs list and initializes last and first pointers.
*/
CacheDeque() {
last = new CacheNode<K, V>();
first = new CacheNode<K, V>();
last.next = first;
first.prev = last;
}
/**
* Puts the node with specified key and value at the end of the deque
* and returns node.
*
* @param key key
* @param value value
* @return added node
*/
CacheNode<K, V> addLast(final K key, final V value) {
CacheNode<K, V> node = new CacheNode<K, V>(key, value);
node.owner = this;
node.next = last.next;
node.prev = last;
node.next.prev = node;
last.next = node;
return node;
}
CacheNode<K, V> addLastNode(final CacheNode<K, V> node) {
node.owner = this;
node.next = last.next;
node.prev = last;
node.next.prev = node;
last.next = node;
return node;
}
/**
* Retrieves and removes the first node of this deque.
*
* @return removed node
*/
CacheNode<K, V> pollFirst() {
CacheNode<K, V> node = null;
if (first.prev != last) {
node = first.prev;
first.prev = node.prev;
first.prev.next = first;
node.prev = null;
node.next = null;
}
return node;
}
/**
* Checks if link to the last node points to link to the first node.
*
* @return is deque empty
*/
boolean isEmpty() {
return last.next == first;
}
}
}
随着缓存淘汰策略的不断发展,针对上诉的三种常见淘汰策略的一些缺陷,大神们又提出许多相对性能要更好的,也更为复杂的新算法。以 LFU 分支为例,针对它存在的两个问题,近年来提出的 TinyLFU 和 W-TinyLFU 算法就往往会有更好的效果。
- TinyLFU(Tiny Least Frequently Used):TinyLFU 是 LFU 的改进版本。为了缓解 LFU 每次访问都要修改计数器所带来的性能负担,TinyLFU 会首先采用 Sketch 对访问数据进行分析,所谓 Sketch 是统计学上的概念,指用少量的样本数据来估计全体数据的特征,这种做法显然牺牲了一定程度的准确性,但是只要样本数据与全体数据具有相同的概率分布,Sketch 得出的结论仍不失为一种高效与准确之间权衡的有效结论。借助Count–Min Sketch算法(可视为布隆过滤器的一种等价变种结构),TinyLFU 可以用相对小得多的记录频率和空间来近似地找出缓存中的低价值数据。为了解决 LFU 不便于处理随时间变化的热度变化问题,TinyLFU 采用了基于“滑动时间窗”(此算法在前面文章中有介绍)的热度衰减算法,简单理解就是每隔一段时间,便会把计数器的数值减半,以此解决“旧热点”数据难以清除的问题。
- W-TinyLFU(Windows-TinyLFU):W-TinyLFU 又是 TinyLFU 的改进版本。TinyLFU 在实现减少计数器维护频率的同时,也带来了无法很好地应对稀疏突发访问的问题,所谓稀疏突发访问是指有一些绝对频率较小,但突发访问频率很高的数据,譬如某些运维性质的任务,也许一天、一周只会在特定时间运行一次,其余时间都不会用到,此时 TinyLFU 就很难让这类元素通过 Sketch 的过滤,因为它们无法在运行期间积累到足够高的频率。应对短时间的突发访问是 LRU 的强项,W-TinyLFU 就结合了 LRU 和 LFU 两者的优点,从整体上看是它是 LFU 策略,从局部实现上看又是 LRU 策略。具体做法是将新记录暂时放入一个名为 Window Cache 的前端 LRU 缓存里面,让这些对象可以在 Window Cache 中累积热度,如果能通过 TinyLFU 的过滤器,再进入名为 Main Cache 的主缓存中存储,主缓存根据数据的访问频繁程度分为不同的段(LFU 策略,实际上 W-TinyLFU 只分了两段),但单独某一段局部来看又是基于 LRU 策略去实现的(称为 Segmented LRU)。每当前一段缓存满了之后,会将低价值数据淘汰到后一段中去存储,直至最后一段也满了之后,该数据就彻底清理出缓存。
当然除了LFU淘汰策略的算法优化,其他的淘汰策略也有相应的改进,如果对这方面感兴趣的小伙伴可以去看看Cache Replacement Policies
扩展功能
不同的缓存方案支持的扩展能力不同,下面列举一下博主所了解的一些扩展能力:
- 加载器:许多缓存都有“CacheLoader”之类的设计,加载器可以让缓存从只能被动存储外部放入的数据,变为能够主动通过加载器去加载指定 Key 值的数据,加载器也是实现自动刷新功能的基础前提(Guava支持)
- 淘汰策略:有的缓存淘汰策略是固定的,也有一些缓存能够支持用户自己根据需要选择不同的淘汰策略。
- 失效策略:要求缓存的数据在一定时间后自动失效(移除出缓存)或者自动刷新(使用加载器重新加载)。
- 事件通知:缓存可能会提供一些事件监听器,让你在数据状态变动(如失效、刷新、移除)时进行一些额外操作。有的缓存还提供了对缓存数据本身的监视能力(Watch 功能)。
- 并发级别:对于通过分段加锁来实现的缓存(以 Guava Cache 为代表),往往会提供并发级别的设置。可以简单将其理解为缓存内部是使用多个 Map 来分段存储数据的,并发级别就用于计算出使用 Map 的数量。如果将这个参数设置过大,会引入更多的 Map,需要额外维护这些 Map 而导致更大的时间和空间上的开销;如果设置过小,又会导致在访问时产生线程阻塞,因为多个线程更新同一个 ConcurrentMap 的同一个值时会产生锁竞争。
- 容量控制:缓存通常都支持指定初始容量和最大容量,初始容量目的是减少扩容频率,这与 Map 接口本身的初始容量含义是一致的。最大容量类似于控制 Java 堆的-Xmx 参数,当缓存接近最大容量时,会自动清理掉低价值的数据。
- 引用方式:支持将数据设置为软引用或者弱引用,提供引用方式的设置是为了将缓存与 Java 虚拟机的垃圾收集机制联系起来。
- 统计信息:提供诸如缓存命中率、平均加载时间、自动回收计数等统计。
- 持久化:支持将缓存的内容存储到数据库或者磁盘中,进程内缓存提供持久化功能的作用不是太大,但分布式缓存大多都会考虑提供持久化功能。
上诉对于缓存的介绍都是基于进程内的缓存,如果是巨石系统我们可以随意选择上面介绍了任意一种高效的缓存方案,但是如果是微服务/分布式的系统下,这些方案就无法满足我们的需求了。举个例子,提供订单能力的服务一共有三台服务器,如果采用上诉的guava或者caffine缓存方案,当一个请求打到A服务器,那么相应的订单数据会缓存到A服务器的进程中,此时B、C服务器中是没有缓存到此次请求的订单数据的,如果下次请求没有打到A服务器而是打到B或者C服务器,此时B、C服务器中是没有此次请求的缓存数据的,那么就会去访问数据库,如果说你的系统QPS不高,这种方案在一定程度上也是可以缓解数据库的压力,但如果是比较极端的情况下或者QPS比较高的场景,在那一时刻,几百上千万的请求打过来,由于B、C服务器中没有缓存相应的订单信息,所有请求全部去查询DB,这会给DB造成极大的压力,甚至会打挂DB。这种情况对于高可用的系统是无法容忍的,那么如何去保证一次请求过来所有服务器都能够感知缓存数据呢?因此我们引入分布式缓存方案来解决这种问题
分布式缓存(引用自《凤凰架构》)
相比起缓存数据在进程内存中读写的速度,一旦涉及网络访问,由网络传输、数据复制、序列化和反序列化等操作所导致的延迟要比内存访问高得多,所以对分布式缓存来说,处理与网络有相关的操作是对吞吐量影响更大的因素,往往也是比淘汰策略、扩展功能更重要的关注点,这决定了尽管也有 Ehcache、Infinispan 这类能同时支持分布式部署和进程内嵌部署的缓存方案,但通常进程内缓存和分布式缓存选型时会有完全不同的候选对象及考察点。
- 从访问的角度来说,如果是频繁更新但甚少读取的数据,通常是不会有人把它拿去做缓存的,因为这样做没有收益。对于甚少更新但频繁读取的数据,理论上更适合做复制式缓存;对于更新和读取都较为频繁的数据,理论上就更适合做集中式缓存。
- 复制式缓存:复制式缓存可以看作是“能够支持分布式的进程内缓存”,它的工作原理与 Session 复制类似。缓存中所有数据在分布式集群的每个节点里面都存在有一份副本,读取数据时无须网络访问,直接从当前节点的进程内存中返回,理论上可以做到与进程内缓存一样高的读取性能;当数据发生变化时,就必须遵循复制协议,将变更同步到集群的每个节点中,复制性能随着节点的增加呈现平方级下降,变更数据的代价十分高昂。
复制式缓存的代表是JBossCache,这是 JBoss 针对企业级集群设计的缓存方案,支持 JTA 事务,依靠 JGroup 进行集群节点间数据同步。以 JBossCache 为典型的复制式缓存曾有一段短暂的兴盛期,但今天基本上已经很难再见到使用这种缓存形式的大型信息系统了,JBossCache 被淘汰的主要原因是写入性能实在差到不堪入目的程度,它在小规模集群中同步数据尚算差强人意,但在大规模集群下,很容易就因网络同步的速度跟不上写入速度,进而导致在内存中累计大量待重发对象,最终引发 OutOfMemory 崩溃。如果对 JBossCache 没有足够了解的话,稍有不慎就要被埋进坑里。
为了缓解复制式同步的写入效率问题,JBossCache 的继任者Infinispan提供了另一种分布式同步模式(这种同步模式的名字就叫做“分布式”),允许用户配置数据需要复制的副本数量,譬如集群中有八个节点,可以要求每个数据只保存四份副本,此时,缓存的总容量相当于是传统复制模式的一倍,如果要访问的数据在本地缓存中没有存储,Infinispan 完全有能力感知网络的拓扑结构,知道应该到哪些节点中寻找数据。 - 集中式缓存:集中式缓存是目前分布式缓存的主流形式,集中式缓存的读、写都需要网络访问,其好处是不会随着集群节点数量的增加而产生额外的负担,其坏处自然是读、写都不再可能达到进程内缓存那样的高性能。
集中式缓存还有一个必须提到的关键特点,它与使用缓存的应用分处在独立的进程空间中,其好处是它能够为异构语言提供服务,譬如用 C 语言编写的Memcached完全可以毫无障碍地为 Java 语言编写的应用提供缓存服务;但其坏处是如果要缓存对象等复杂类型的话,基本上就只能靠序列化来支撑具体语言的类型系统(支持 Hash 类型的缓存,可以部分模拟对象类型),不仅有序列化的成本,还很容易导致传输成本也显著增加。举个例子,假设某个有 100 个字段的大对象变更了其中 1 个字段的值,通常缓存也不得不把整个对象所有内容重新序列化传输出去才能实现更新,因此,一般集中式缓存更提倡直接缓存原始数据类型而不是对象。相比之下,JBossCache 通过它的字节码自审(Introspection)功能和树状存储结构(TreeCache),做到了自动跟踪、处理对象的部分变动,用户修改了对象中哪些字段的数据,缓存就只会同步对象中真正变更那部分数据。
如今Redis广为流行,基本上已经打败了 Memcached 及其他集中式缓存框架,成为集中式缓存的首选,甚至可以说成为了分布式缓存的实质上的首选,几乎到了不必管读取、写入哪种操作更频繁,都可以无脑上 Redis 的程度。也因如此,之前说到哪些数据适合用复制式缓存、哪些数据适合集中式缓存时,笔者都在开头加了个拗口的“理论上”。尽管 Redis 最初设计的本意是 NoSQL 数据库而不是专门用来做缓存的,可今天它确实已经成为许多分布式系统中无可或缺的基础设施,广泛用作缓存的实现方案 - 从数据一致性角度说,缓存本身也有集群部署的需求,理论上你应该认真考虑一下是否能接受不同节点取到的缓存数据有可能存在差异。譬如刚刚放入缓存中的数据,另外一个节点马上访问发现未能读到;刚刚更新缓存中的数据,另外一个节点访问在短时间内读取到的仍是旧的数据,等等。根据分布式缓存集群是否能保证数据一致性,可以将它分为 AP 和 CP 两种类型(在“分布式事务”中已介绍过 CAP 各自的含义)。此处又一次出现了“理论上”,是因为我们实际开发中通常不太会把追求强一致性的数据使用缓存来处理,可以这样做,但是没必要(可类比 MESI 等缓存一致性协议)。譬如,Redis 集群就是典型的 AP 式,有着高性能高可用等特点,却并不保证强一致性。而能够保证强一致性的 ZooKeeper、Doozerd、Etcd 等分布式协调框架,通常不会有人将它们当为“缓存框架”来使用,这些分布式协调框架的吞吐量相对 Redis 来说是非常有限的。不过 ZooKeeper、Doozerd、Etcd 倒是常与 Redis 和其他分布式缓存搭配工作,用来实现其中的通知、协调、队列、分布式锁等功能。
分布式缓存与进程内缓存各有所长,也有各有局限,它们是互补而非竞争的关系,如有需要,完全可以同时把进程内缓存和分布式缓存互相搭配,构成透明多级缓存(Transparent Multilevel Cache,TMC),如下图所示。先不考虑“透明”的话,多级缓存是很好理解的,使用进程内缓存做一级缓存,分布式缓存做二级缓存,如果能在一级缓存中查询到结果就直接返回,否则便到二级缓存中去查询,再将二级缓存中的结果回填到一级缓存,以后再访问该数据就没有网络请求了。如果二级缓存也查询不到,就发起对最终数据源的查询,将结果回填到一、二级缓存中去。
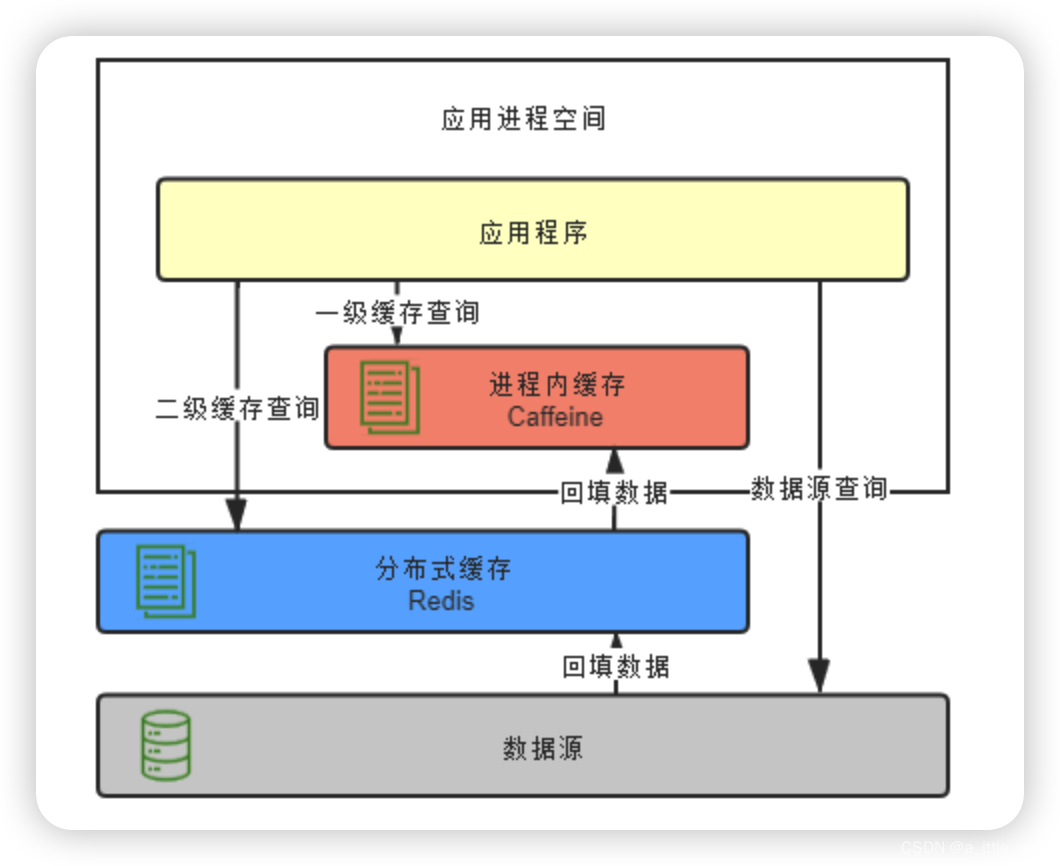
尽管多级缓存结合了进程内缓存和分布式缓存的优点,但它的代码侵入性较大,需要由开发者承担多次查询、多次回填的工作,也不便于管理,如超时、刷新等策略都要设置多遍,数据更新更是麻烦,很容易会出现各个节点的一级缓存、以及二级缓存里数据互相不一致的问题。必须“透明”地解决以上问题,多级缓存才具有实用的价值。一种常见的设计原则是变更以分布式缓存中的数据为准,访问以进程内缓存的数据优先。大致做法是当数据发生变动时,在集群内发送推送通知(简单点的话可采用 Redis 的 PUB/SUB,求严谨的话引入 ZooKeeper 或 Etcd 来处理),让各个节点的一级缓存自动失效掉相应数据。当访问缓存时,提供统一封装好的一、二级缓存联合查询接口,接口外部是只查询一次,接口内部自动实现优先查询一级缓存,未获取到数据再自动查询二级缓存的逻辑。
缓存风险
按照“没有银弹”理论的角度来看,任何技术栈都是有利有弊,同样的使用缓存也会带来一些问题,如果:缓存一致性、缓存穿透、缓存击穿、缓存雪崩等。
缓存一致性
缓存一致性问题指的就是如何保证db的数据和缓存中数据的一致性,而常见的解决方案有如:Cache Aside、Read Through、Write Through、Write Behind、Double Delete等,由于篇幅问题,这里博主就不过多介绍这几种方案了,如果对这几种方案感兴趣的话可以去看Consistency between Redis Cache and SQL Database
缓存穿透、缓存击穿、缓存雪崩
这三种问题已经有很多博主也做过详细说明,这里贴一篇文章how to solve the problem of redis cache avalanche breakdown and peneration,感兴趣的小伙伴可以去看看