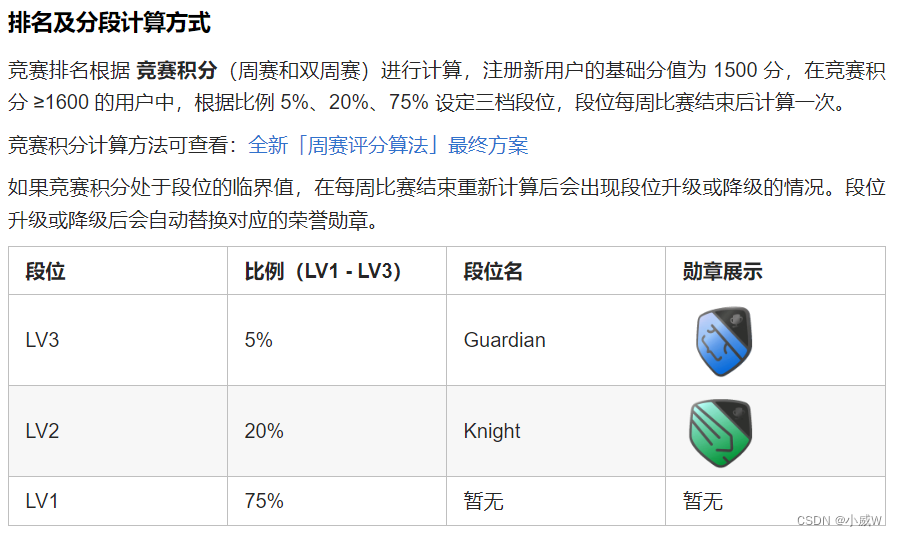
题目链接:力扣

解题思路:贪心,尽可能地找到下一跳能够跳到的最远距离,这样到达终点时,所需跳跃次数最少
以nums = [2,3,1,1,4,2]为例:
- 以当前位置begin作为起跳点,能够跳跃的最远距离为m,那么接下来的m个位置都能作为下一次的起跳点。从这m个位置中选择能够跳远最远的点最为下一次起跳点。result保存最终跳跃次数
- 初始时在位置0,num[0]=2,那么接下来的2个位置,都能作为下一次的起跳点 [2,3,1,1,4,2],可以选择3和1,选择3能够跳跃的最远索引为4,选择1能够跳跃的最远索引为3,显然选择3能够跳跃最远,即选择索引为1的位置作为下一跳的起跳点
- 从上次选择的起跳点作为新的begin,重复步骤1,直到能够跳跃到最后,每次跳跃时result自增1
- 上一次的起跳点的索引为1,num[1]=3,接下来的3个位置都能作为下一次跳跃的起跳点。[2,3,1,1,4,2],显然选择4,即从索引为4的位置开始跳能够跳的最远,当选择从索引为4的位置跳时,能够跳跃的最后,结束,result即所求。
- 一个小优化:其实可以不用从上一次选择的起跳点的下一个位置作为本次起跳点的开始位置,而是直接将上一次起跳范围的结束位置作为本次起跳点的开始位置:
- 上一次的起跳点选择范围为:[2,3,1,1,4,2],本次起跳的范围[2,3,1,1,4,2]
- 其中本次起跳的范围可以直接为:[2,3,1,1,4,2],即将上一次跳跃的最远距离end作为下一次起跳的开始位置begin。而不用上一次选择的起跳点的下一个位置作为begin,这样可以减少选择起跳点的循环次数
- 比如上一次的起跳范围为: [begin1,a1,a2,a3,end1],假如选择a1作为起跳点能够跳跃的最远距离为m,则下一跳的跳跃范围为[begin1,a1,a2,a3,end1,b1,b2,...,m],仔细观察,可以发现a2,a2,end1这三个位置在本次跳跃中的位置选择可以不用考虑,因为从这些位置出发,能够跳跃的最远位置肯定小于m(因为选择a2此能够跳跃最远m,其他位置能够跳跃的距离都比m小),所以本次跳跃的范围只需要从[begin1,a1,a2,a3,end1,b1,b2,...,m],这些位置中选择就可以了。
- 解题的关键在于:下一跳的起跳点的选择,当前位置begin能够跳跃的最远距离为m,则begin后面的m个位置都能够最后下一次的起跳点,从这m个位置中选择能够跳跃最远的位置作为新的起跳点。其中可以使用begin,end保存下一跳能够选择的起跳点,end=begin+m,下一条的起跳点范围为(begin,end],左开右闭区间。
- 选择每次起跳点时可以使用for选择,从(begin,end]区间进行选择
- 每完成一次跳跃,更新begin和end,并令result+1
- 当下一跳能够跳跃的最远距离大于等于nums.length-1,算法结束
AC代码:
class Solution {
public static int jump(int[] nums) {
int result = 0;
//下一跳的选择区间[begin,end],左闭右闭区间
//能够选择的跳跃区间的左边界
int begin = 0;
//能够选择的跳跃区间的右边界
int end = 0;
while (end < nums.length - 1) {
int nextEnd = 0;
for (int i = begin; i <= end; i++) {
//从[begin,end]区间中计算能够跳跃的最远位置,并更新左边界
nextEnd = Math.max(nextEnd,i+nums[i]);
}
//下一次能够选择的起跳点的开始位置
begin = end+1;
//下一次能够选择的起跳点的结束位置
end= nextEnd;
result++;
}
return result;
}
}优化
在上述while循环包含的for循环中,begin和end的更新都是从前往后更新的,可以优化掉外层的循环,只需要在完成一次跳跃时更新下一次能够跳跃的最远距离,使用一个for循环从前往后遍历:
- 初始时,最小跳跃次数result=0,end=0,nextEnd=0;
- 每遍历一个位置更新一次能够跳跃的最远距离nextEnd=Math.max(nextEnd,i+nums[i])。
- 当i==end时,说明上一次的跳跃的边界结束了,开始下一次跳跃点的选择,这个时候更新end=nextEnd,result++
AC代码
class Solution {
public static int jump(int[] nums) {
int result = 0;
int end = 0;
int nextEnd = 0;
for (int i = 0; i < nums.length - 1; i++) {
nextEnd = Math.max(nextEnd, i + nums[i]);
if (i == end) {
end = nextEnd;
result++;
}
}
return result;
}
}上面两种算法的时间复杂度都是O(n),效率一样。不过后面这种算法做法更加简洁