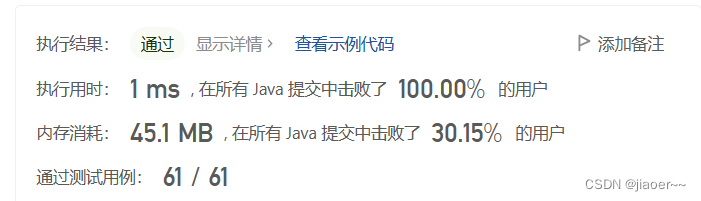
20. 有效的括号

思路:这里用模拟栈的方法会更好理解,也就是我们每次遇到朝左方向的三种类型的时候,就加入相反方向的右括号到result栈中。由于栈是一个先进后出的方式,所以我们会有一个判断stack当前为不为空,和stack[-1]是不是和当前循环到的括号相同。如果说相同,那就说明我们之前已经加入过对应的左括号,就可以直接pop,如果不同,就说明这个字符并不是按照顺序来排列的,比如说[(])。 当我们循环到“]"的时候,会发向stack[-1]是')'的,但是我们之前也确实加入过‘]"这个括号,但是他们两个这里并不相等,说明他们并不是按照对应的括号类型来排列的,所以也就不是有效的括号,就可以直接return False了。
代码:
def isValid(self, s: str) -> bool:
stack = []
for i in s:
if i=='{':
stack.append("}")
elif i=='(':
stack.append(')')
elif i=='[':
stack.append(']')
elif not stack or stack[-1]!=i:
return False
else:
stack.pop()
return len(stack)==01047. 删除字符串中的所有相邻重复项

比较简单的一道题目
思路:还是用栈的方法来记录,因为这里栈可以帮助我们记录上一次的元素是什么
如果说当前元素不在栈中,那么我们就入栈,如果在栈中,我们需要同时判断当前元素是不是栈的最后一个元素,也就是我们上次加入的元素。如果是,那么就构成了相邻的重复项,这里进行栈的pop操作。那么如果不等于,就说明当前元素和上一个不是相邻重复项,正常添加即可
代码:
def removeDuplicates(self, s: str) -> str:
stack = []
for x in s:
if x in stack and x==stack[-1]:
stack.pop()
else:
stack.append(x)
return ''.join(stack)150. 逆波兰表达式求值


这里刚开始看可能会比较懵逼,看下图的这个例子了解什么是逆波兰式子
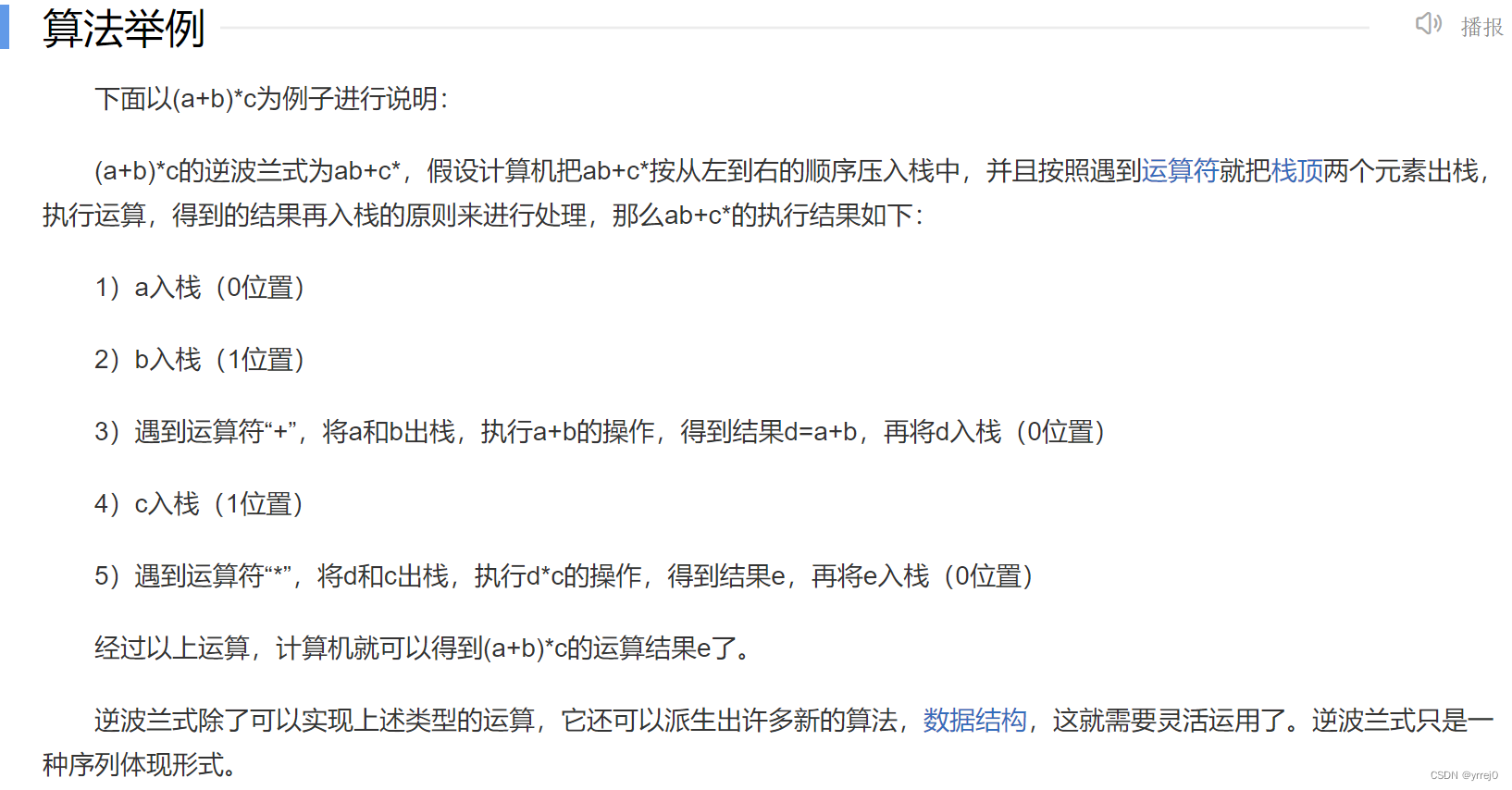
逆波兰式就是把算法运算符放到后面操作,计算机认为这个很简单识别。
思路:
当我们判断当前元素如果是算法运算符号,我们就用一个result去记录栈中上两个数字的对应的算法操作符,比如当前是+,那么我们的result = stack[-1] + stack[-2].这里+和*都是按照这个顺序,但是当我们碰到-和/的时候,这里是用stack[-2] - stack[-1] 或者是stack[-2]/stack[-1].
然后将栈中的前两个元素弹出,因为我们已经记录过他们之间的操作了,所以不需要他们了,然后将result加入栈中,知道遇见下一个操作符然后重复上面的步骤。
代码:
stack = []
for x in tokens:
if x=="+":
result = stack[-1] + stack[-2]
elif x=='-':
result = stack[-2]-stack[-1]
elif x=='/':
result = stack[-2]/stack[-1]
elif x=='*':
result = stack[-1]*stack[-2]
else:
stack.append(int(x))
continue
stack.pop()
stack.pop()
stack.append(int(result))
return stack[-1]