不同路径（力扣）动态规划 JAVA

news2024/9/24 17:17:10

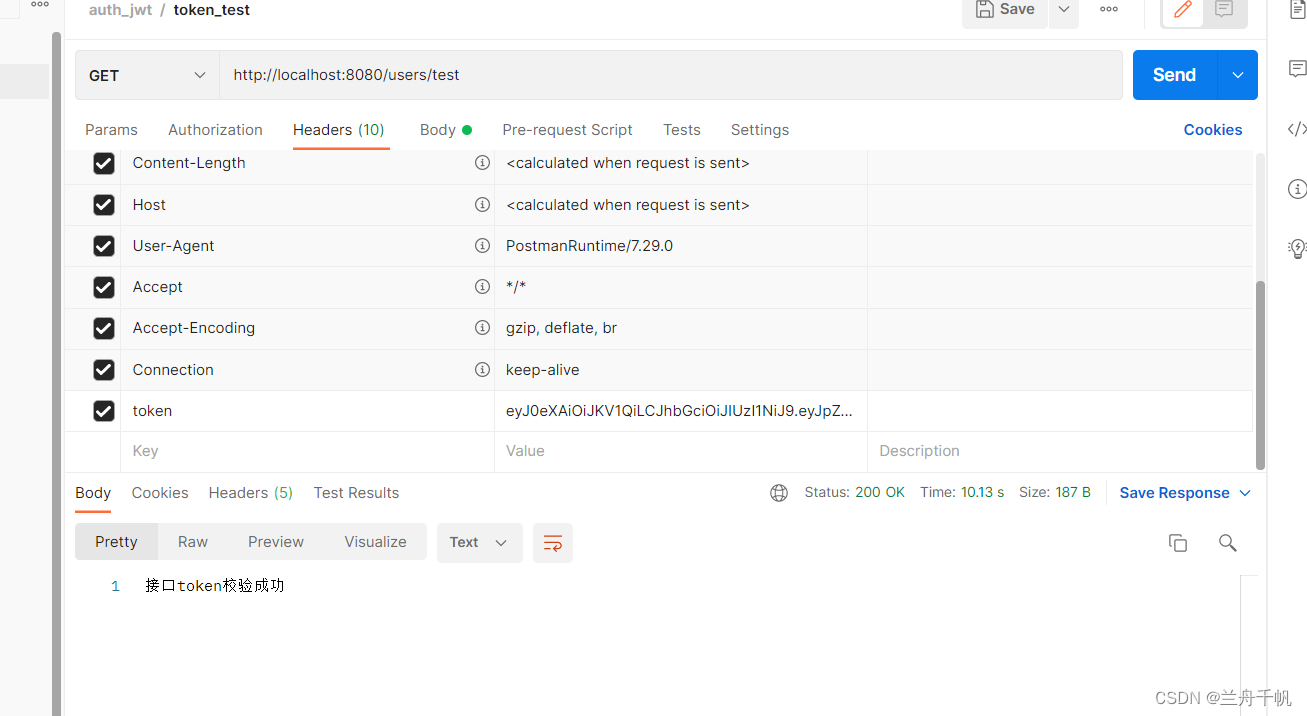
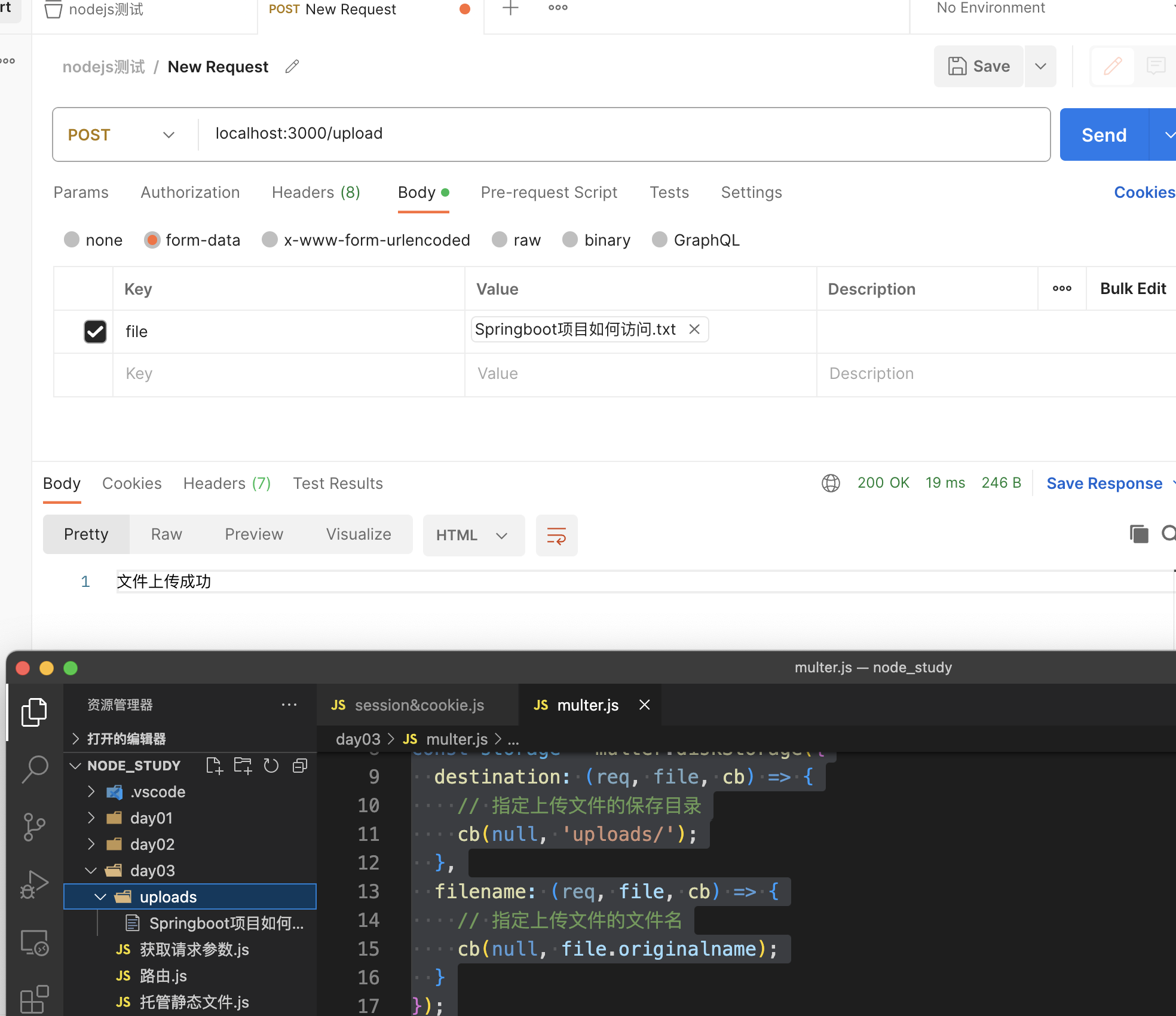
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

在这里插入图片描述

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

解题思路：

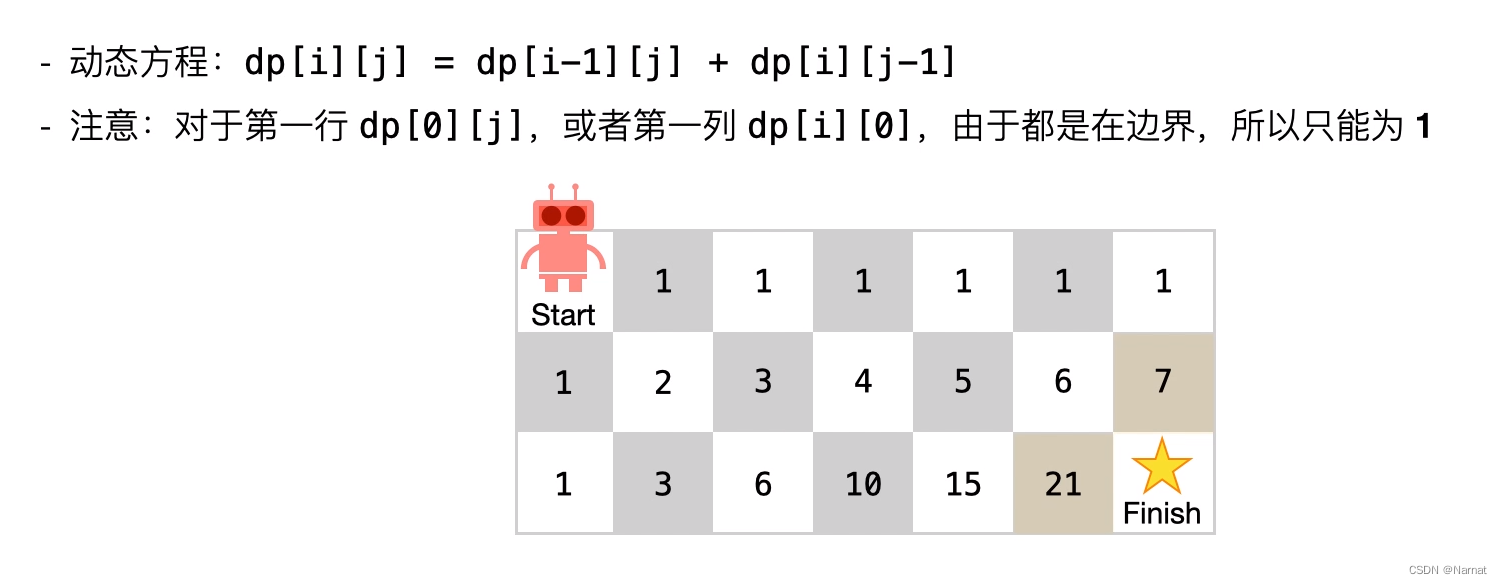
在这里插入图片描述
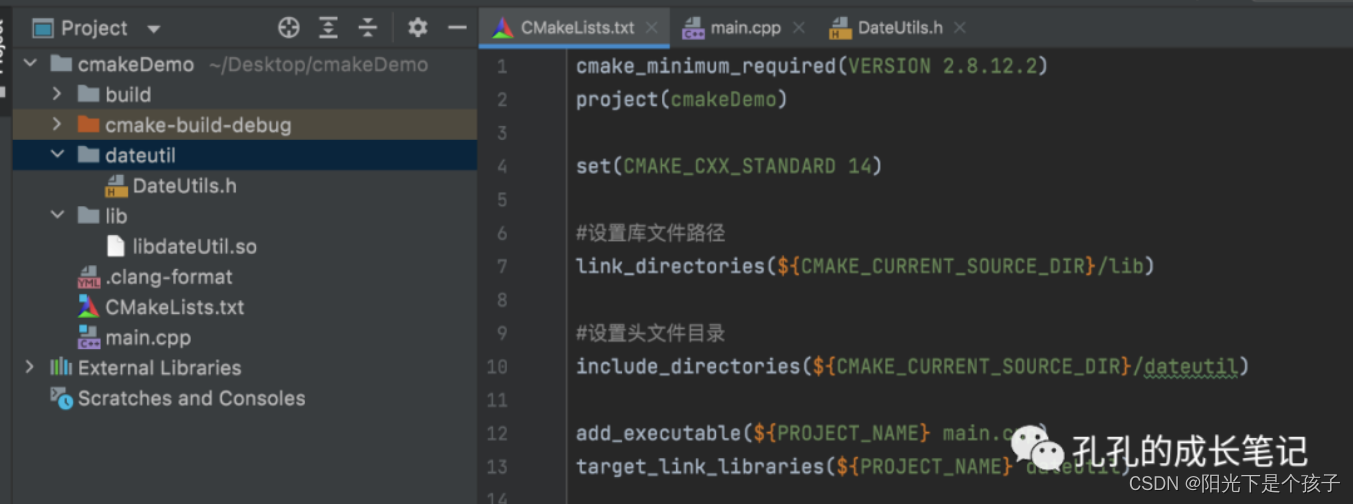
1.题目网格完全可以用数组模拟

2.到达网格每个位置的方法数，等于到达此位置左边，和上边位置的方法数的和（要么由左边来，要么上边来）

3.边界都为1，因为到达边界的方法只有一条

4.由递推公式可得出，新位置方法数，由上边和左边方法相加得来，所以从上往下一行一行更行是符合要求的

朴素代码：

class Solution {
    public int uniquePaths(int m, int n) {
       int dp[][] = new int [m][n];//建立网格
       for(int i = 0; i < m; i ++) dp[i][0] = 1;
       for(int j = 0; j < n; j ++) dp[0][j] = 1;//边界为1,路径只有一种可能
       
       for(int i = 1; i < m; i ++)
    	   for(int j = 1; j < n; j ++) {
    		   dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    	   }
       return dp[m - 1][n - 1];
    }
}

在这里插入图片描述

优化代码：

class Solution {
    public int uniquePaths(int m, int n) {
       int dp[] = new int [n];//建立网格
       for(int i = 0; i < n; i ++) dp[i] = 1;
       
       for(int i = 1; i < m; i ++)
    	   for(int j = 1; j < n; j ++) {
    		   dp[j] = dp[j] + dp[j - 1];
    	   }
       return dp[n - 1];
    }
}