- 第3章 词法分析
- 3.1 词法分析器的功能和结构
- 3.2 状态转换图
- 3.3 正则文法 和 正则表达式
- 3.4 有限自动机 DFA与NFA
- 测试
第3章 词法分析
重点:① 词法分析器的输入、输出;② 用于识别符号的状态转移图的构造;③ 根据状态转移图实现词法分析器
难点:词法的正规文法表示、正规表达式表示、状态转移图表示,以及它们之间的转换。
3.1 词法分析器的功能和结构
-
词法分析器的功能:
把构成源程序的字符串转换成“等价的”单词序列(根据词法规则识别及组合单词,进行词法检查;对数字常数完成数字字符串到二进制数值的转换;删去空格和注释等不影响程序语义的字符) -
词法分析器 包含:
预处理子程序:用于去除无用的空白、跳格、回车、换行等编辑性字符;区分标号区
扫描器:在扫描缓冲区中识别单词符号
扫描缓冲区:存放经过预处理的比较规范的字符串
输入缓冲区:扫描器调用预处理子程序,将源程序输入到输入缓冲区中,预处理子程序读取输入缓冲区中的字符进行文本的预处理 -
扫描缓冲区
扫描器通过两个指针(起点指示器与搜索指示器)进行扫描,起点指示器指向马上要识别的单词的开始位置,搜索指示器从起点指示器的位置开始,寻找单词的结尾
存在问题:① 缓冲区内容用完后,需要等待新的输入,应该避免类似等待;② 一个单词可能会被缓冲区分隔开,即单词的一部分在缓冲区中,另一部分没有读入,如果需要读入的话,需要将当前缓冲区中内容覆盖,单词的前半部分就无了,而且无法执行超前搜索
解决方案:将缓冲区划分为两个半区(即设置双缓冲区),扫描器每次只读取一个半区的长度,如果搜索指示器指到当前半区的末尾,且还未找到单词末尾,则扫描器将后续内容读入另一半区,搜索指示器从另一半区开始继续寻找单词末尾;此外还需要限定 单词长度不能超过半区的长度
具体实现方式:使用带标记的双缓冲区,每个缓冲区末尾都设置"EOF"区域结束标识
缓冲区长度÷2 = 缓冲半区的长度 = 程序设计语言允许的标识符最大长度
3.2 状态转换图
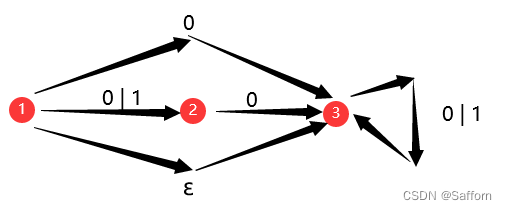
- 状态转换图:
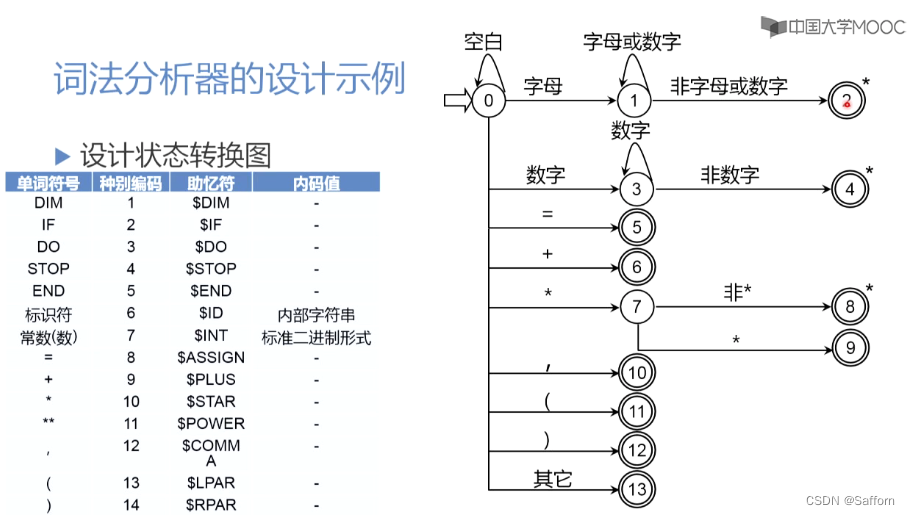
- 实现(以状态0-1-2为例):
/* 状态0 -> 状态1 -> 状态2 */
int code, value;
strToken = ""; //存放构成单词符号
GetChar(); GetBC(); // 读取字符 跳过空白符
if(IsLetter()) //判断输入是否为字母
begin /* 状态1 */
while (IsLetter() or IsDigit())
begin /* 状态1循环 */
Concat(); GetChar(); //拼接单词字符,继续读入
end
/* 状态2 */
Retract(); //回退最后的非字母数字输入
code := Reserve(); //判断是关键字还是用户自定义标识符
if (code = 0) //是用户自定义标识符
begin
value := InsertId(strToken); //把strToken插入到符号表中
return ($ID, value); //返回标识符在符号表中的位置和对应值
end
else //是关键字
return (code, NULL);
end
- 正则表达式 转换为 状态转换图
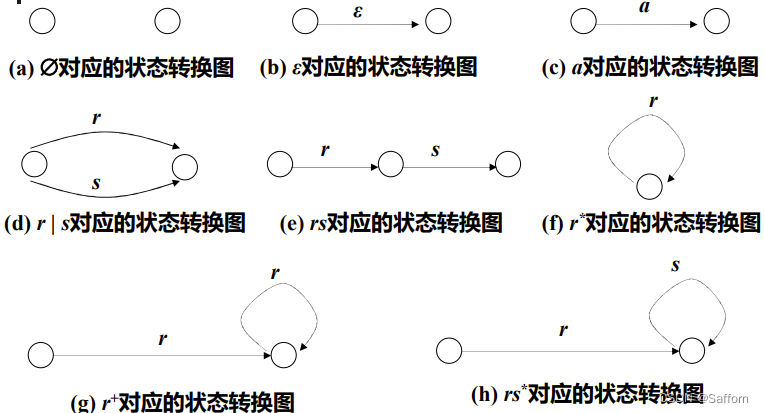
3.3 正则文法 和 正则表达式
正则表达式 = 正则式
正则集 = 正则语言(简写为 “语言”)
- 对于给定字母表
∑
\sum
∑ :
- ε 和
∅
\varnothing
∅ 都是
∑
\sum
∑ 上的正则表达式,它们所表示的正则文法为 {ε} 和
∅
\varnothing
∅
理解:ε 既是一个字,也是一个正则表达式,它代表的正则集(语言)为{ε},该集合中有一个字,是ε,该字长度为0,不包含任何字符; ∅ \varnothing ∅既是一个集合,也是一个正则表达式,它代表的正则集为{ },该集合为空 - (定义) 任何
a
∈
∑
a\in\sum
a∈∑,
a
a
a是
∑
\sum
∑上的正则表达式,它所表示的正则集为
{
a
}
\{a\}
{a}
理解: a a a 既是字母表 ∑ \sum ∑中的一个字符,也是一个由一个字符a所构成的长度为1的字/字符串,也是一个正则表达式,所表示的正则语言 L ( a ) L(a) L(a)为 { a } \{a\} {a} - 设
e
1
e_1
e1和
e
2
e_2
e2都是
∑
\sum
∑上的正则表达式,所表示的正则文法分别为
L
(
e
1
)
L(e_1)
L(e1)和
L
(
e
2
)
L(e_2)
L(e2),则
① ( e 1 ∣ e 2 ) (e_1|e_2) (e1∣e2)为正则表达式,它表示的语言为 L ( e 1 ) ∪ L ( e 2 ) L(e_1)\cup L(e_2) L(e1)∪L(e2)
② ( e 1 ⋅ e 2 ) (e_1·e_2) (e1⋅e2)为正则表达式,它表示的语言为 L ( e 1 ) L ( e 2 ) L(e_1) L(e_2) L(e1)L(e2)
③ ( e 1 ) (e_1) (e1)为正则表达式,它表示的语言为 ( L ( e 1 ) ) ∗ (L(e_1))^* (L(e1))∗
④ 仅由有限次使用上述规则构造的表达式 是 ∑ \sum ∑ 上的正则w表达式 - 如果正则表达式 r 与 s 表示的正则语言相同,即
L
(
r
)
=
L
(
s
)
L(r)=L(s)
L(r)=L(s),则称 r 与 s 等价,也称 r 与 s 相等,记作 r = s
问题 证明 b(ab)*=(ba)* → L(b(ab)*) = L(b)L((ab)*) = L(b)(L(ab))* = L(b)(L(a)L(b))* = {b}{ab}*,同理等式右侧表示的语言同左,等式得证
- ε 和
∅
\varnothing
∅ 都是
∑
\sum
∑ 上的正则表达式,它们所表示的正则文法为 {ε} 和
∅
\varnothing
∅
3.4 有限自动机 DFA与NFA
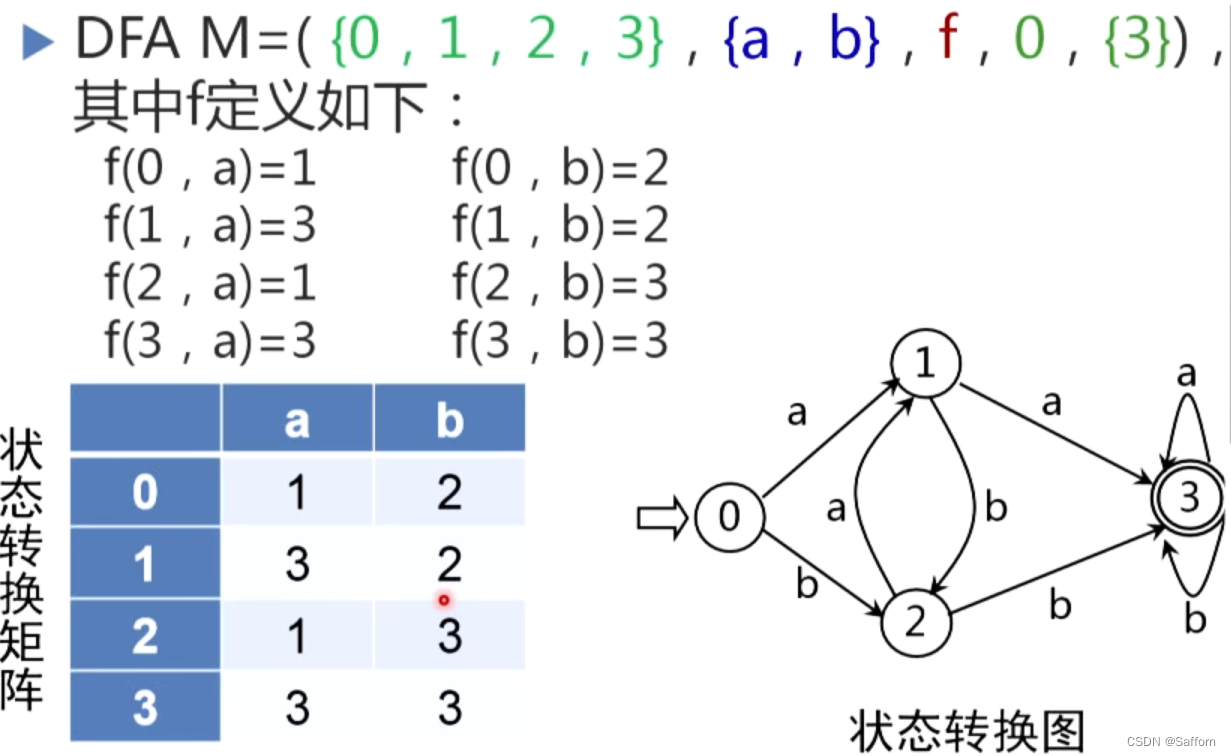
- 确定有限自动机M是一个五元组
M
=
(
S
,
∑
,
f
,
S
0
,
F
)
M=(S, \sum, f, S_0, F)
M=(S,∑,f,S0,F)
S S S:有穷状态集合
∑ \sum ∑:输入字母表(有穷)
f f f:状态转换函数, f ( s , a ) = s ′ f(s, a)=s' f(s,a)=s′表示当前状态 s s s,输入字符为 a a a,将状态转换到下一状态 s ′ s' s′
S 0 S_0 S0: S 0 ∈ S S_0 \in S S0∈S,是唯一的初态
F F F:终止状态集合, F ⊆ Q F\subseteq Q F⊆Q
- 非确定有限自动机 NFA,其定义与DFA类似,NFA M是一个五元组
M
=
(
S
,
∑
,
f
,
S
0
,
F
)
M=(S, \sum, f, S_0, F)
M=(S,∑,f,S0,F),其中不同点如下:
f f f:状态转换函数,为 S ∗ ∑ ∗ → 2 S S*\sum^* \rightarrow 2^S S∗∑∗→2S(从一个状态读入一个字符,其后继状态不唯一)
S 0 S_0 S0: S 0 ⊆ S S_0 \subseteq S S0⊆S是非空的初态集(NFA可以有多个初态)
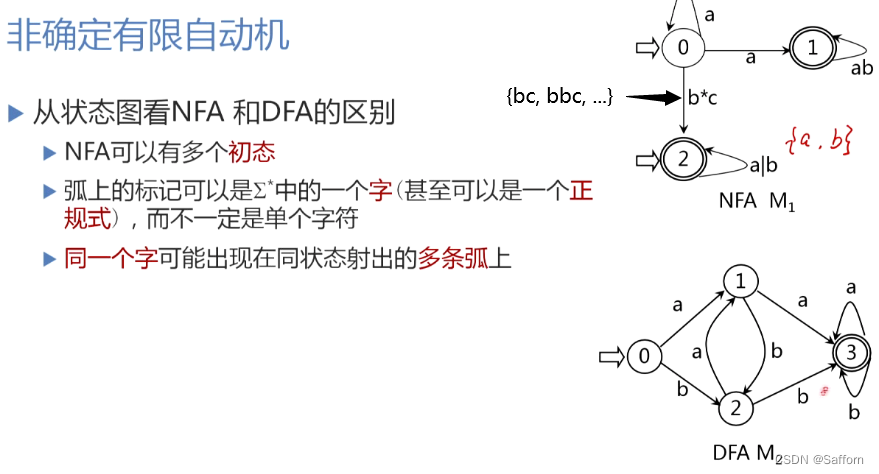
- DFA 与 NFA 比较

测试
-
证明 (a*b*)* = (a|b)*
-
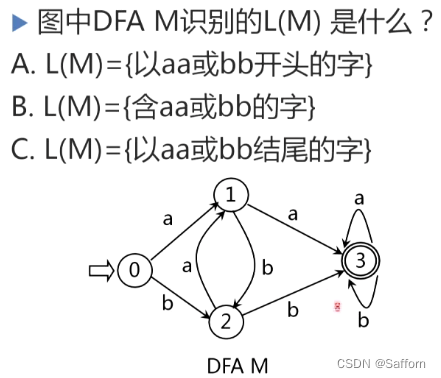
答:B,含有aa或bb的字 -
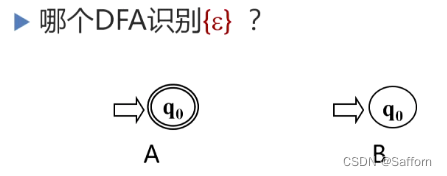
答:A初态即终态,识别空字ε后可以由初态到达终态,即A可以识别 {ε};B图不含有终态,不能识别任何字符,包括空字ε,即B可以识别{}空集 -
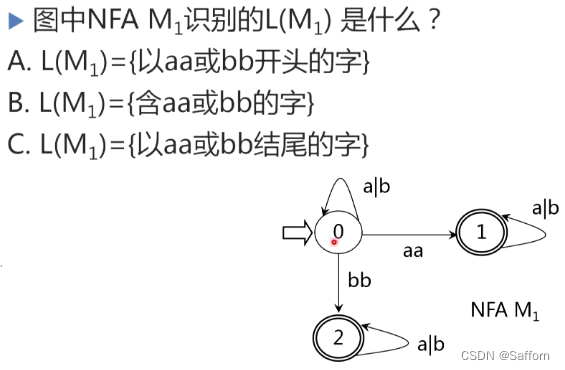
答:B,含有aa或bb的字 -
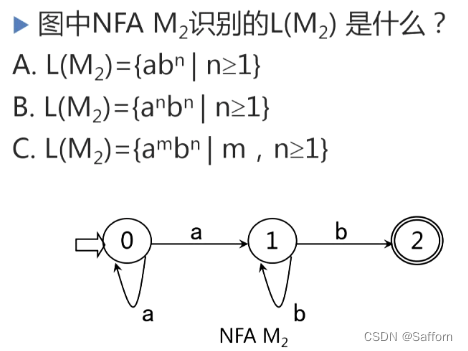
答:C -
构造 ε|(0|1)01* | 0+的状态转换图