背景
在这里我们主要介绍YOLO 系列的相关目标检测算法,从最开始的YOLO v1 一直到 YOLO v5。本文也借鉴了其他文档和原始论文。总结下来这五个方法的演进线路如下表格所示。
| 对比维度 | YOLO v1 | YOLO v2 | YOLO v3 | YOLO v4 | YOLO v5 |
|---|---|---|---|---|---|
| backbone | VGG | darknet19 | darknet53 | darknet53 | darknet53 |
| 是否有anchor | 否 | 是 | 是 | 是 | 是 |
| anchor 个数 | 0 | 多个(5) | 多个(9) | 多个 | 多个 |
| 是否multi-head | 否 | 否 | 是 | 是 | 是 |
| GT和anchor关系 | 1对1 | 1对1 | 1对1 | 1对多 | 1对多 |
| GEO Loss | MSE | MSE | MSE | CIoU | CIoU |
接下来我们将完整的介绍YOLO v1的方法,然后我们将从上述表格的几个方面来介绍演进路线。
YOLO v1
一开始原始的YOLO v1主打的就是一个快,他基本的思想就是将图像分层若干个块,每个块负责预测一个物体。当我们输入一张图片的时候,经过一些列CNN的操作,他就会变成7X7的feature map,那么我们将feature map上的每一个点分别负责预测一个框,这就是最简单的YOLO v1的思想。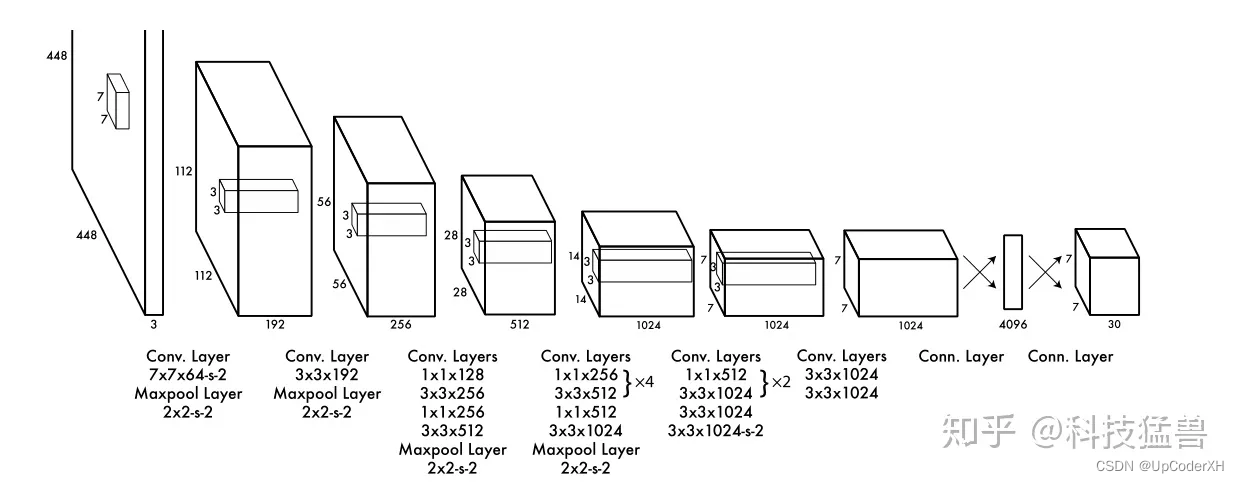
整体结构
YOLO v1的整体结构如上图所示,他给整个系列的YOLO 定下了基调。针对得到的7X7的feature map,他将feature map最终映射成为了BX7 X7X30的维度。
那么如何理解这里的30呢?=5*2+20,这里的20代表我们最后预测物体类别已经有20个类别,5代表的是(c,x,y,w,h),c表示的是置信度分数,xywh分别表示的是中心点左边和宽高。2表示的是预测一个大物体,一个小物体。
Loss 函数设计
yolo v1的损失函数设计如下图所示。其中第一行和第二行代表的是geo loss。第三行代表的是有物体的置信度损失,第四行代表的是没有物体的置信度损失(三四相当于一个带权的损失函数)第五行代表的是具体物体类别的损失函数。

Backbone
backbone的演进思路基本上就是VGG->Darknet,我们具体来看Darknet为什么比VGG效果更好
- 删除了7x7的卷积,整体替换为3x3的和1x1的卷积,这样子在相同感受野的前提下,网络结构可以做的更深,并且参数量更小
- 引入量很多1x1的卷积
- 可以增加深度,增加非线性
- 降维/升维
- 跨channel的信息融合
- 减少卷积参数
- 分辨率也有调整,从一开始的224调整为448(推理的时候416),推理的时候之所以要变为奇数是先验,因为大物体大部分是放在图像中心,奇数个刚好由一个grid来负责预测,否则会将物体拆分到四个grid。
- pooling层替换成了stride=2的卷积层,增加模型的可学习性,减少模型的信息损失。

Anchor
YOLO系列从v2开始引入了anchor的概念,v2的时候每个grid有五个anchor,v3的时候由于更改为multi-head的结构,每个head的每个grid有3个anchor。v4和v5基本遵从v3的设计。
-
Q1:v1的时候如何每个grid分工?
- Answer:我们判断bbox的中心点落在哪个grid内,我们就让哪个grid来负责预测该bbox
-
Q2:v2/v3的多个anchor是怎么得到的?
- Answer:根据数据集的bbox集合,通过聚类的方式产出,聚类得到的anchor集合如下图所示。
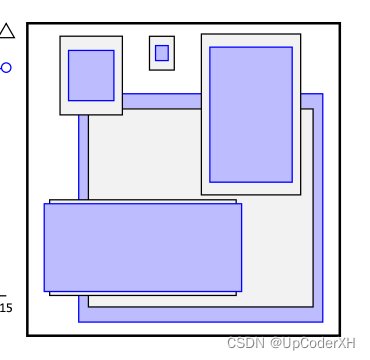
- Answer:根据数据集的bbox集合,通过聚类的方式产出,聚类得到的anchor集合如下图所示。
-
Q3:每个grid有多个anchor,那么gt和anchor的关系如何对应?
- Answer:在v2和v3 这里是看grid和对应的哪个anchor的IoU最大,就将对应anchor的gt 设置为该bbox,也就是一个gt bbox只能由一个anchor来预测,在v4修改为可以由多个anchor来预测,只需要IoU大于指定的阈值就可以,这样子也改善了正负样本的比例。
Multi-Head
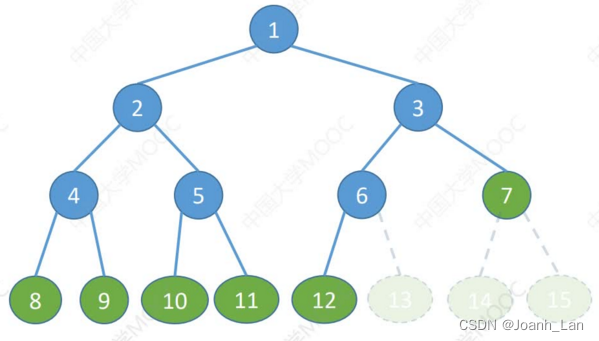
在v2中我们通过每个grid预测多个anchor来解决目标遗漏的问题,但是针对小目标的检测,v2仍然不是十分友好,因此,从yolov3开始引入了multi-head的概念,引入了不同分辨率的,13x13的预测大物体,26x26的负责预测中物体,52x52的负责预测小物体。每个分辨力对应的anchor大小也是不一样的。基本结构图如下图所示
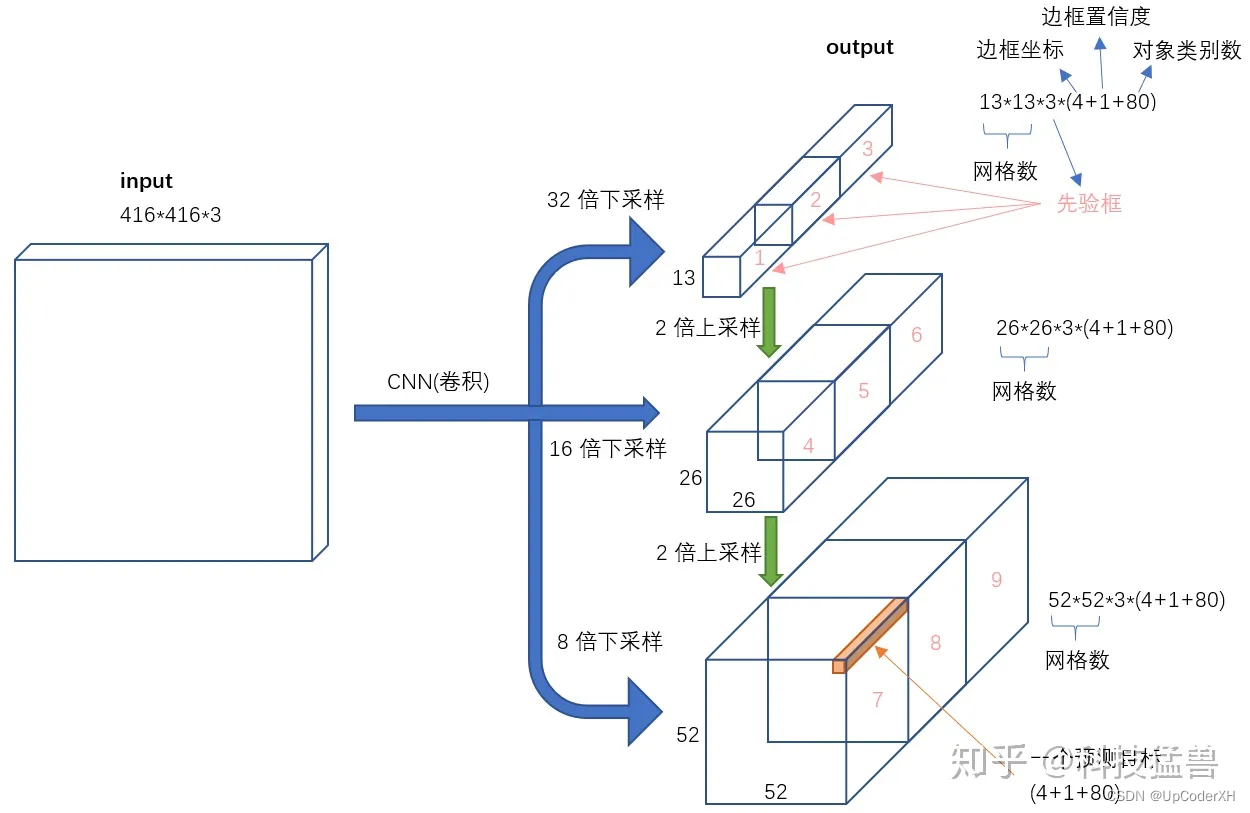
GEO Loss
上面在介绍v1的时候,我们介绍了v1的相关GEO loss,他是直接预测center x、y和对应的width和height。
但是这样子会导致整体预测的范围变大,变得较难收敛,因此从v2开始,预测的目标变成了偏移量tx,ty,th,tw,它的定义如下图所示,预测的目标是tx/y/h/w他表示的皈依化后的偏移量。在推理的时候我们根据下面的公式可以计算得到bx,by。
- 红色的是真值计算
- 蓝色的是推理时候的推算,
c
x
,
c
y
,
p
h
,
p
w
c_x,c_y,p_h,p_w
cx,cy,ph,pw都是对应的anchor尺寸。
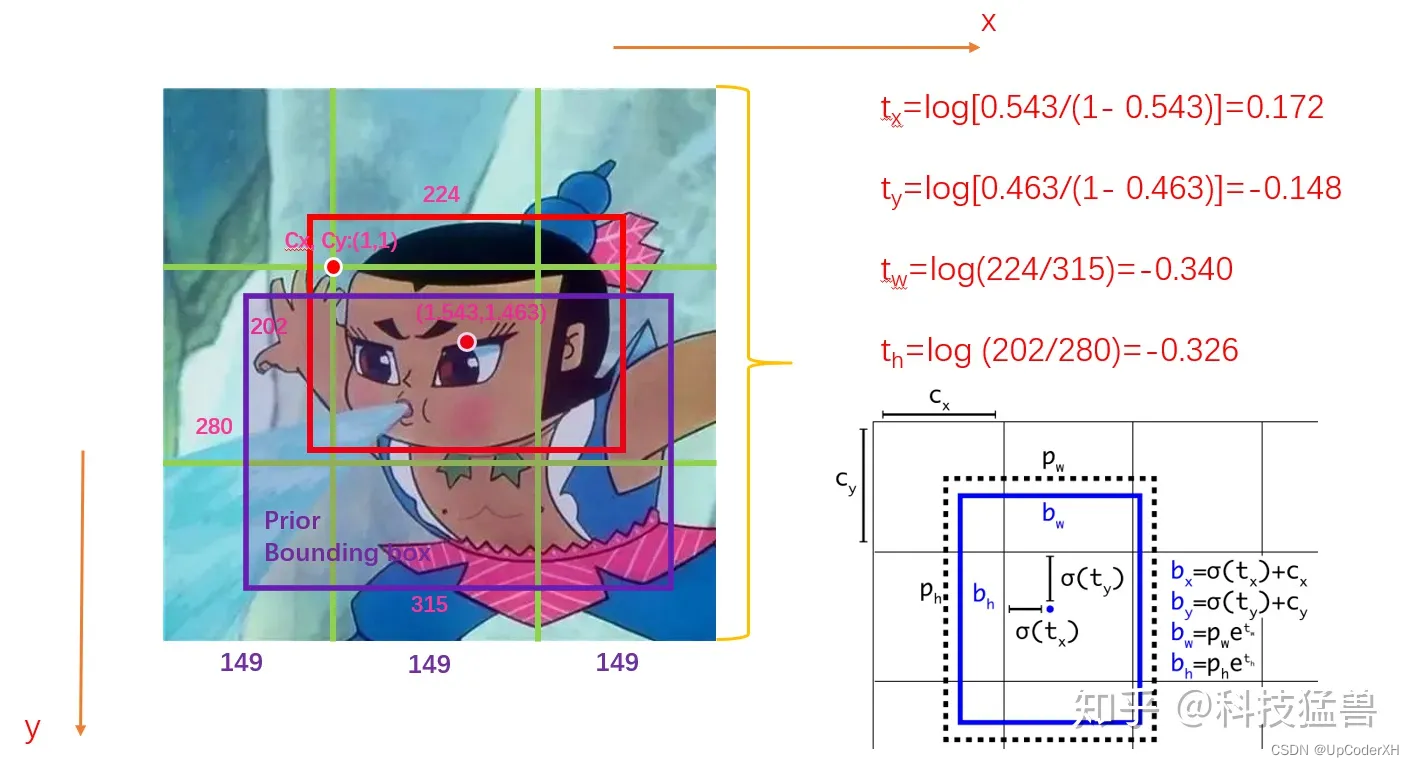

v1、v2、v3整体上还是使用的是基于MSE的损失函数,从v4开始使用基于IoU的损失函数来优化位置距离,这里我们主要介绍三种IoU Loss,GIoU、DIoU和CIoU
IoU Loss
原始的IoU 损失函数定义如下所示,通过使用这种IoU 损失函数,可以将评估指标和优化函数对齐。不过原始的IoU损失函数问题在于
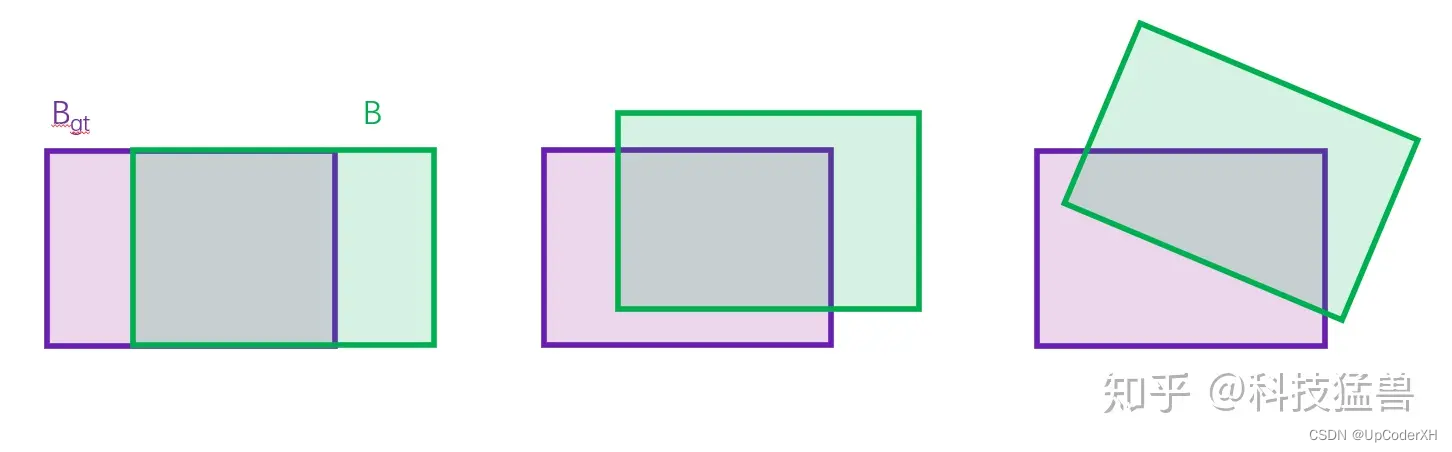
- 当两个bbox没有overlap 的时候失去的优化的目标。
- 不能范围两个之间的重合度(距离),如下图所示,三者的IoU是一样的 但是明显左边的优化更好一点。
L I o U = 1 − B 交 B g t B 并 B g t L_{IoU}=1-\frac{B 交 B_{gt}}{B 并 B_{gt}} LIoU=1−B并BgtB交Bgt
GIoU Loss
先说定义,定义如下所示,其中
C
C
C代表的含义是两个组成的最小外接矩阵。这样子可以确保两者没有相交的时候,也可以持续优化。
L
g
=
1
−
I
o
U
+
∣
C
−
B
并
B
g
t
∣
∣
C
∣
L_g=1-IoU+\frac{|C-B 并 B_{gt}|}{|C|}
Lg=1−IoU+∣C∣∣C−B并Bgt∣
DIoU Loss
上述GIoU loss的问题在于不好直接优化,当两者没有挨着的时候,我们知道沿着中心点的线进行优化是最快的,因此引入了DIoU,它的公式如下所示。
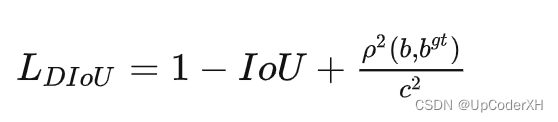
DIoU在下述的这个case中在第三项是没有区别的,因此引入了CIoU
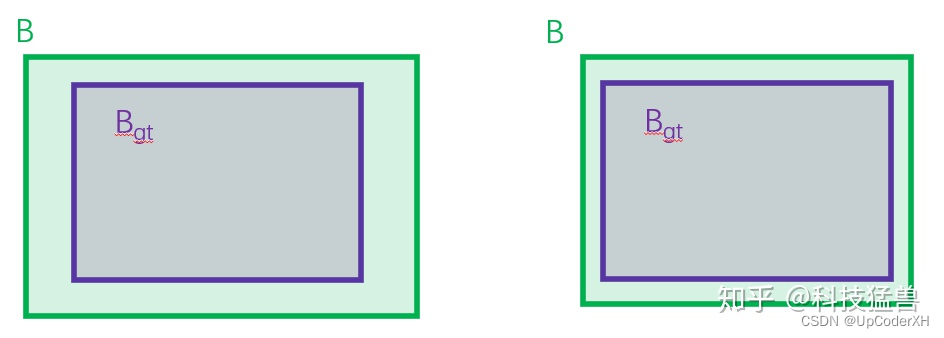
CIoU Loss
惩罚项的定义如下所示
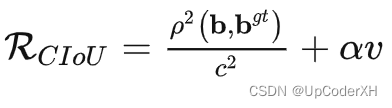







![商业海外社交媒体营销10步指南 [2023]](https://img-blog.csdnimg.cn/img_convert/ec6d5dd11ec57e4b36919ac308f113cb.png)