数据结构–二叉树的性质
二叉树常考性质
常见考点1: 设非空二叉树中度为0、1和2的结点个数分别为 n 0 、 n 1 和 n 2 ,则 n 0 = n 2 + 1 n_0、n_1和n_2,则n_0= n_2 +1 n0、n1和n2,则n0=n2+1
n 0 = n 2 + 1 \color{red}n_0= n_2 +1 n0=n2+1(叶子结点比二分支结点多一个)
假设树中结点总数为n,则
n
=
n
0
+
n
1
+
n
2
n
=
n
1
+
2
n
2
+
1
\begin{array}{c}\mathrm{n}=n_0+n_1+n_2\\\mathrm{n}=n_1+2n_2+1\end{array}
n=n0+n1+n2n=n1+2n2+1
树的结点数 = 总度数 + 1 \color{green}树的结点数=总度数+1 树的结点数=总度数+1
下式减上式可得:
n
0
=
n
2
+
1
\color{red}n_0= n_2 +1
n0=n2+1
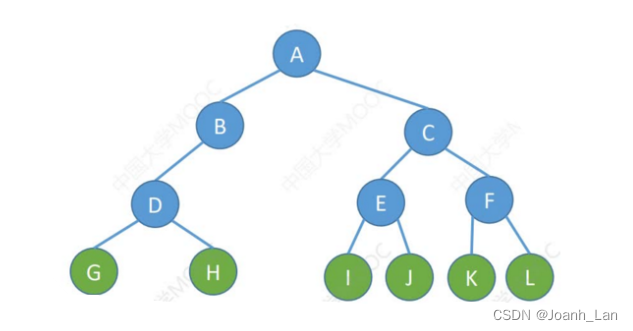
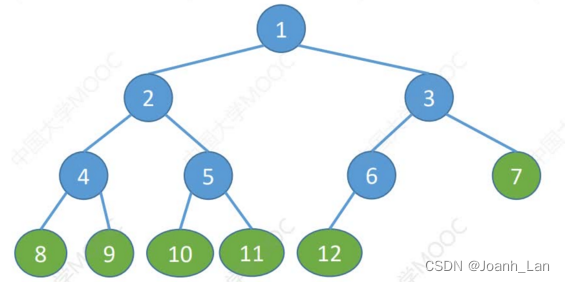
常见考点2:
二叉树第i层至多有
2
i
−
1
2^{i-1}
2i−1个结点( i≥1)
m叉树第i层至多有
m
i
−
1
m^{i-1}
mi−1个结点( i≥1)

常见考点3: 高度为h的二叉树至多有 2 h − 1 2^h -1 2h−1个结点(满二叉树)
高度为h的m叉树至多有 m h − 1 m − 1 \frac{m^{h}-1}{m-1} m−1mh−1 个结点
等比数列求和公式: a + a q + a q 2 + ⋯ + a q n − 1 = a ( 1 − q n ) 1 − q \text{等比数列求和公式:}a+a\text{q}+aq^2+\cdots+aq^{n-1}=\frac{a(1-qn)}{1-q} 等比数列求和公式:a+aq+aq2+⋯+aqn−1=1−qa(1−qn)
完全二叉树的常考性质
常见考点1: 具有n个(n>0)结点的 完全二叉树的高度 h 为 ⌈ log 2 ( n + 1 ) ⌉ 或 ⌊ log 2 n ⌋ + 1 \color{red}完全二叉树的高度h为 \lceil\log_2(n+1)\rceil\text{或}\lfloor\log_2n\rfloor+1 完全二叉树的高度h为⌈log2(n+1)⌉或⌊log2n⌋+1
高为h的满二叉树共有 2 h − 1 2^h -1 2h−1个结点高为 h − 1 h-1 h−1的满二叉树共有 2 h − 1 − 1 2^{h-1} -1 2h−1−1个结点
2 h − 1 − 1 < n ≤ 2 h − 1 2 h − 1 < n + 1 ≤ 2 h h − 1 < log 2 ( n + 1 ) ≤ h h = ⌈ log 2 ( n + 1 ) ⌉ \begin{gathered} 2^{h-1}-1<n\leq2^{h}-1 \\ 2^{h-1}<n+1\leq2^h \\ h-1<\log_{2}(n+1)\leq h \\ h=\color{red}\lceil\log_{2}(n+1)\rceil \end{gathered} 2h−1−1<n≤2h−12h−1<n+1≤2hh−1<log2(n+1)≤hh=⌈log2(n+1)⌉
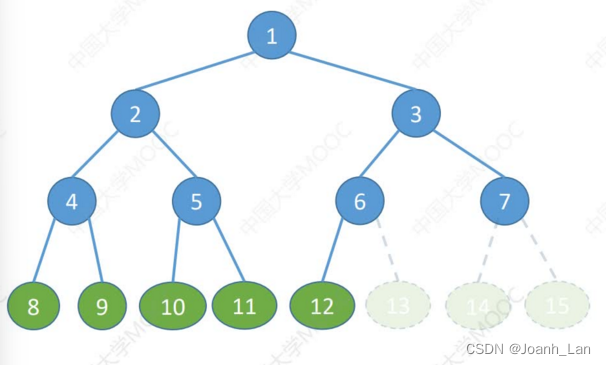
高为h-1的满二叉树共有
2
h
−
1
−
1
2^{h-1}-1
2h−1−1个结点
高为h的完全二叉树
至少
2
h
−
1
2^{h-1}
2h−1个结点
至多
2
h
−
1
2^h -1
2h−1个结点
2 h − 1 ≤ n < 2 h h − 1 ≤ log 2 n < h h = ⌊ log 2 n ⌋ + 1 \begin{aligned}2^{h-1}&\leq n<2^h\\\\h-1&\leq\log_2n<\text{h}\\\\h&=\color{red}{\lfloor\log_2n\rfloor}+1\end{aligned} 2h−1h−1h≤n<2h≤log2n<h=⌊log2n⌋+1
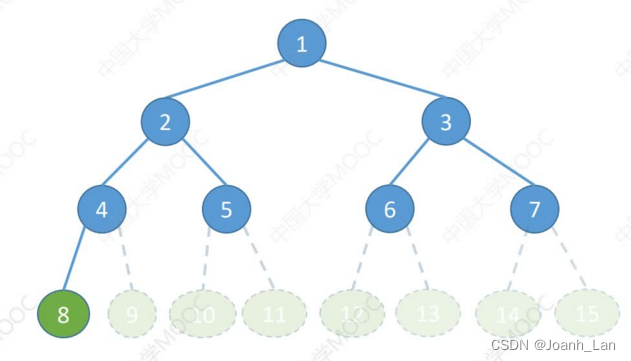
第 i 个结点所在层次为 ⌈ log 2 ( n + 1 ) ⌉ 或 ⌊ log 2 n ⌋ + 1 \color{red}\text{第 }i\textit{ 个结点所在层次为}\lceil\log_2(n+1)\rceil\text{或}\lfloor\log_2n\rfloor+1 第 i 个结点所在层次为⌈log2(n+1)⌉或⌊log2n⌋+1
常见考点2: 对于完全二叉树,可以由的结点数n推出度为0、1和2的结点个数为
n
0
、
n
1
,
和
n
2
,
n_0、n_1,和n_2,
n0、n1,和n2,
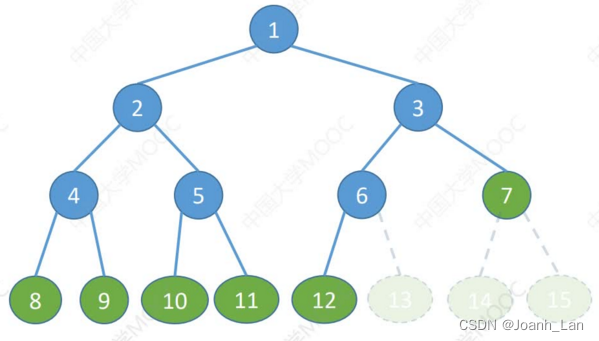
完全二叉树最多只有一个度为1的结点,即
n 1 = 0 或1 n 0 = n 2 + 1 → n 0 + n 2 一定是奇数 \begin{array}{l}n_1=0\text{或1}\\n_0=n_2+1\rightarrow n_0+n_2\text{ 一定是奇数}\end{array} n1=0或1n0=n2+1→n0+n2 一定是奇数
若完全二叉树有 2 k 个(偶数)个结点,则必有 n 1 = 1 , n 0 = k , n 2 = k − 1 \color{red}若完全二叉树有2k个(偶数)个结点,则必有n_1=1,n_0 = k,n_2 = k-1 若完全二叉树有2k个(偶数)个结点,则必有n1=1,n0=k,n2=k−1
若完全二叉树有 2 k − 1 个(奇数)个结点,则必有 n 1 = 0 , n 0 = k , n 2 = k − 1 \color{red}若完全二叉树有2k-1个(奇数)个结点,则必有n_1=0,n_0= k, n_2 = k-1 若完全二叉树有2k−1个(奇数)个结点,则必有n1=0,n0=k,n2=k−1
知识点回顾与重要考点
二叉树:
- n 0 = n 2 + 1 n_0= n_2+ 1 n0=n2+1
- 第 i 层至多有 2 i − 1 2^{i-1} 2i−1个结点( i≥1)
- 高度为 h 的二叉树至多有 2 h − 1 2^h - 1 2h−1 个结点
完全二叉树:
- 具有 n 个(n>0)结点的完全二叉树的高度 h 为 ⌈ log 2 ( n + 1 ) ⌉ 或 ⌊ log 2 n ⌋ + 1 \lceil\log_2(n+1)\rceil\text{或}\lfloor\log_2n\rfloor+1 ⌈log2(n+1)⌉或⌊log2n⌋+1
- 对于完全二叉树,可以由的结点数 n 推出为 0、1 和 2 的结点个数为 n 0 、 n 1 和 n 2 n_0、n_1和n_2 n0、n1和n2 (突破点:完全二叉树最多只会有一个度为1的结点)