注： 以后的方程中如未说明，x表示机器人自身位置，y表示路标（地图中的点），观测数据用z表示，将这个过程看做离散的，则时间从1到…
轨迹：由x构成的集合；

1. 运动与观测

1.1 通用运动方程

$x_k=f(x_{k-1},u_k,w_k)$

• 上式表示$x_{k-1}到x_k$的过程，$f$是通用的，$u_k$表示输入(运动传感器的读数)：例如机器人自身的轮速计等，$w_k$表示误差

参数化举例：
设机器人在二维平面中运动，则位姿可以由x,y,和转角来描述，即$x_k=[x,y,\theta {]}_k^T$,同时机器人身上的编码器等传感器可得$u_k=[\Delta x,\Delta y,\Delta \theta {]}_k^T$，则带入上述运动方程可得：

$${\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]}_k={\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]}_{k-1}+{\left[\begin{array}{c}\Delta x\\ \Delta y\\ \Delta \theta \end{array}\right]}_k+w_k$$

1.2 通用观测方程

$z_{k,j}=h(y_j,x_k,v_{k,j})$

• 上式表示在 $x_k$ 上看到路标$y_j$ 产生了观测数据$z_{k,j}$，$v_{k,j}$表示误差

参数化举例：

设机器人装有一个2D激光雷达，能读到距离$r$ 和 夹角$\theta$ 两个值，在2D世界中，记一个landmark(路标点)为 $y=[p_x,p_y{]}^T$ 观测数据为 $z=[r,\varphi {]}^T$， 则观测方程可如下：
$$\left[\begin{array}{c}r\\ \varphi \end{array}\right]=\left[\begin{array}{c}\sqrt{(p_x-x{)}^2+(p_y-y{)}^2}\\ \arctan (\frac{p_y-y}{p_x-x})\end{array}\right]+v$$
对视觉SLAM而言，观测方程就是 “对路标点拍摄后，得到了图
像的（具体是图像中的像素）” 的过程

1.3 对SLAM的认识

知道运动测量的数据$u$，传感器的数据$z$ ，求解定位$x$ 和建图 $y$ 的问题
$\Downarrow \Downarrow \Downarrow$

状态估计问题：带有噪声的数据$⟹$内部隐藏的状态变量

噪声： 分为 $Guassian$ 和 $Non-Guassian$
两个方程： 分为 $Linear$ 和 $Non-Linear$
**线性高斯系统(LG)**是无偏的(样本均值近似等于总体均值)，可以用KF求解；
非线性非高斯(NLNG)系统，现在主要用EKF->粒子滤波器->图优化（时间顺序），图优化占资源，且效果明显好，优先选择。

2. 三维运动

2.1 旋转与平移

$a和a‘$分别是两个坐标系下的同一个点，它们在各自空间用坐标和基底表示如下：

$$\left[\begin{array}{ccc}{e}_1& e_2& e_3\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]=\left[\begin{array}{ccc}{e}_1^{‘}& e_2^{‘}& e_3^{‘}\end{array}\right]\left[\begin{array}{c}{a}_1^{‘}\\ a_2^{‘}\\ a_3^{‘}\end{array}\right]$$
变换如下：

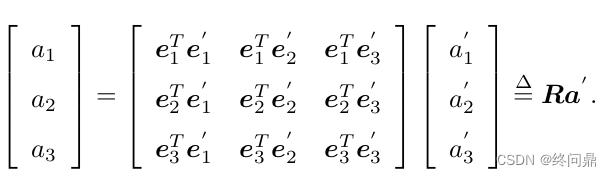
中间的$R$ 称为旋转矩阵，是行列式为1的正交阵，定义$R$ 如下：
$SO(n)$ = {$R\in {\mathbb{R}}^{nxn}|R{R}^T=I,det(R)=1$}

解释：$SO(n)$是特殊正交群(Special Orthogonal Group)。

则带上平移量的变换为：
$a^{\prime }=Ra+t$ 相反旋转为： $a=R^T{a}^{\prime }-t=R^{-1}{a}^{\prime }-t$

2.2 变换矩阵

$T$(Transform matrix)

避免如上表示多次变换的形式过长，引入变换矩阵T，如$b=T_{1}ac=T_{2}b⟹c=T_2{T}_{1}a$

它可以定义如下(引入齐次坐标后)：

$SE(3)$ = { $T=\left[\begin{array}{ccc}R& t& \\ 0^T& 1& \end{array}\right]\in {\mathbb{R}}^{4x4}|R\in SO(3),t\in {\mathbb{R}}^3$}

同样$T^{-1}$ 表示一个反向的变换，不区分齐次坐标$\tilde{a}$和非齐次坐标$a$的区别，默认是符合我们运算的那种。

2.3 矩阵知识补充

• 正交矩阵的转置$=$它的逆
• 转置性质$(AB{)}^T=B^T{A}^T$
• 反对称矩阵 $A=-A^T$
• 实矩阵乘以它的转置得到的矩阵是实对称矩阵
• 矩阵可以用来解方程，直接求逆： $Ax=b⟹x=b{A}^{-1}$ (费时间)
• 用QR分解: $Ax=b\Rightarrow A=QR\Rightarrow QRx=b\Rightarrow Rx=Q^{T}b$ (Q是N阶正交阵，R是上三角)(省一半时间)

2.4 旋转向量

$SO(3)$用9个量表示旋转，正交且$det(R)$为1是它的约束，$SE(3)$也是一样的。因此不够紧凑、约束条件对求解的限制等都成为了它的问题。

旋转向量： 一个三维向量，用一个旋转轴$n$ 和 旋转角 $\theta$ 表示.
变换矩阵        \;\;\; 在这种表示下 一个旋转向量+一个平移向量就可以表示。
转换关系:      \;\; 通过罗德里格斯(Rodrigues’s Formula)公式

\qquad \qquad \qquad\qquad \qquad 旋转向量 $⟹$ 旋转矩阵

1. 设一旋转轴$n$，角度 $\theta$ 的旋转表示为 $n\theta$，和旋转矩阵$R$ 表示转换如下：

$R=\cos \theta \cdot I+(1-\cos \theta )n{n}^T+\sin \theta \cdot n$^

• 其中^表示向量的反对称运算，参考视觉SLAM14讲中外积的表示

\qquad \qquad \qquad\qquad \qquad 旋转矩阵 $⟹$ 旋转向量

2. 如下：
   $\theta =\arccos (\frac{tr(R)-1}{2})$
   $Rn=n$

• 转轴在旋转前后不发生变化。转轴 n 是矩阵 R 特征值 1 对应的特征向量。求解此方程，再归一化，就得到了旋转轴。

2.5 欧拉角

\qquad 直观，但是有奇异性—“万向锁”（Gimbal Lock），调试观察时可转为欧拉角，一般不用于计算，以下旋转是有先后顺序的，以一种为例(Z-Y-X)，表示如下：

$yaw$ - 偏航角 - 绕$Z$ 轴转
$pitch$ - 俯仰角 - 绕旋转之后的$Y$ 轴转
$roll$ - 偏航角 - 绕旋转之后的$X$ 轴转

2.6 四元数

Quaternion，消除欧拉角的奇异性且紧凑的表示法。以地球纬度$\pm 90^o$为例，仅用两个坐标无法表示。四元数用四个数表示旋转。一个实部，三个虚部(或向量)。
$q=q_0+q_{1}i+q_{2}j+q_{3}k$
满足
$$f(x)=\{\begin{array}{l}{i}^2=j^2=k^2=-1\\ ij=k,ji=-k\\ jk=i,kj=-i\\ ki=j,ik=-j\end{array}$$

用四元数表示旋转
\qquad 假设某个旋转是绕单位向量 $n=[nx,ny,nz{]}^T$ 进行了角度为 $\theta$ 的旋转，那么这个旋转的四元数形式为：
$$q=\left[\begin{array}{c}\cos \frac{\theta }{2},n_x\sin \frac{\theta }{2},n_y\sin \frac{\theta }{2},n_z\sin \frac{\theta }{2}\end{array}\right](1)$$

\qquad 要对点$p=[x,y,z]$进行旋转，轴角法$n,\theta$，表示这个旋转过程如下：

1. 首先用式1表述这个点(三个虚轴)
   $p=[0,x,y,z]$
2. 旋转后的点$p^{\prime }$
   $p^{\prime }=qp{q}^{-1}$

• 计算结果实部为0，故是纯虚四元数，虚部三个分量表示旋转后的3D点的坐标。
• 同理，四元数$⟺$ 旋转向量 $⟺$ 旋转矩阵 也可相互转化，较为容易。

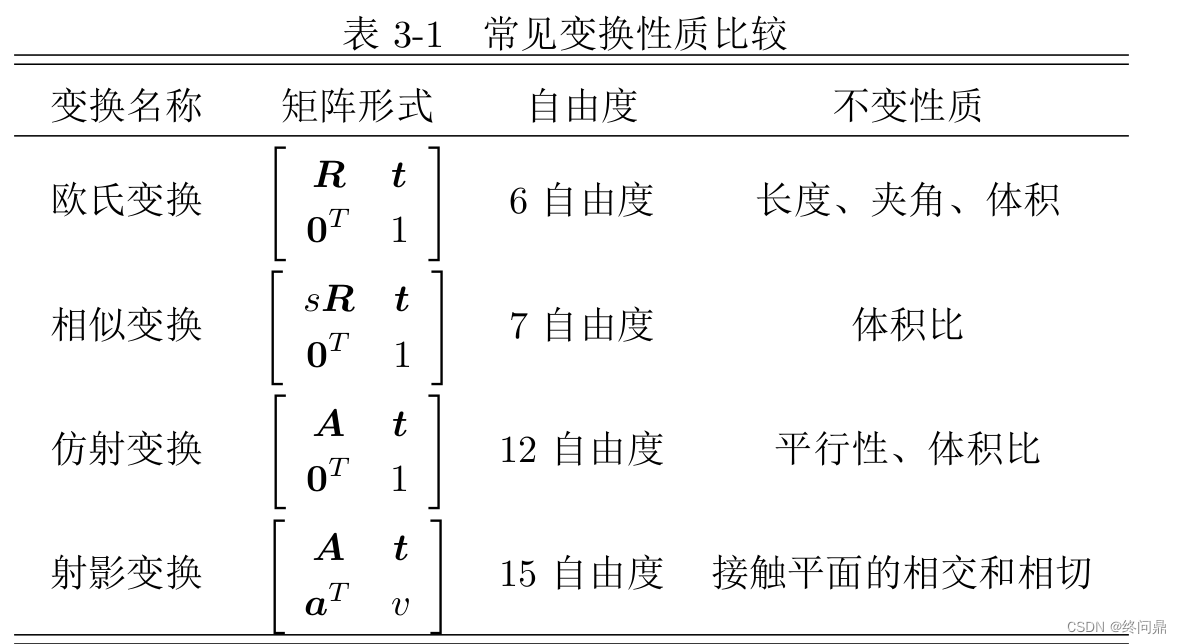
2.7 其他变换

以上都是欧式变换，除此之外还存在如下几种SLAM中可能用到的变换

1. **相似变换：**允许物体均匀缩放；
2. 仿射变换；
3. **射影变换；**等
   

3. 编程基础

3.1 链接库说明

静态库.a和动态库.so：所有库都是一些函数打包后的集合，差别在于静态库每次被调用都会生成一个副本，而共享库则只有一个副本，更省空间。

库+头文件的意义: 库文件是一个压缩包，里头带有编译好的二进制函数。为了让别人（或
者自己）使用这个库，我们需要提供一个头文件，基本是这个库的使用说明啦。因此，对于库
的使用者，只要拿到了头文件和库文件，就可以调用这个库。

构建动态库：在CMakeLists.txt中，动态库的编译如下:参数1是名称，3是要被编译成的文件

add_library( slam_shared SHARED SLAM.cpp )

使用该库：如下：

add_executable(useHello useHello.cpp)
target_link_libraries(useHello slam_shared)

3.2 eigen库

是一个很有意思的库，纯用头文件编写，没有.so,.a等库，所以调用的时候只要保证头文件的路径正确即可。在很多资料中头文件包含是这样的<Eigen/xxxxx>，实际上这个路径不在我们的搜索路径中，三种解决办法：

1. 到/usr/include/eigen3/Eigen/下将eigen3改名为Eigen，且将原Eigen的文件全部上移一层到Eigen下
2. 将该路径加入头文件搜索路径中,在VSCODE中很容易实现；或在CmakeLists.txt中加入include_directories( "/usr/include/eigen3" )
3. 改一个头文件包含方式，前边<eigen3/Eigen/xxxxxx>即可

如果eigen有关的编译报错，直接找报错信息的大写部分就大概能知道。
用eigen库表示一般的几种表示旋转的函数