目录

一、有向图 157

1.1有向图的定义及相关术语 157

1.2有向图的实现 158

二、拓扑排序 159

2.1检测有向图中的环 160

2.1.1检测有向图中环API设计 160

2.1.2检测有向环实现 161

2.2基于深度优先顶点排序 162

2.2.1顶点排序API设计

2.2.2顶点排序实现的原理过程

2.2.3顶点排序代码的实现及测试 162、163、164

三、加权无向图 165

3.1加权无向图边的表示---加权的边实现 166

3.2加权无向图边的表示---无向图的实现 167

四、最小生成图 168

4.1最小生成树定义及相关约定 168

4.2最小生成树原理---切分定理 169

4.2.1树的性质

4.2.2切分定理

4.3贪心算法 170

4.4Prim算法 171

4.4.1Prim算法API设计

4.4.2Prim算法的实现原理 172  

4.4.3Prim算法的代码实现及测试173、174、175

4.5kruskal算法 176

4.5.1kruskal算法API设计 

4.5.2kruskal算法的实现原理 177

4.5.3kruskal算法代码实现及测试 178、179

五、加权有向图 180

5.1加权有向图边的表示 180

5.2加权有向图的实现 181

六、最短路径182

6.1最短路径定义及性质 182

6.2最短路径树API设计 182

6.3松弛技术 183

6.4Dijstra算法实现及测试 184、185、186

---

一、有向图 157

图的边是有方向的

1.1有向图的定义及相关术语 157

 

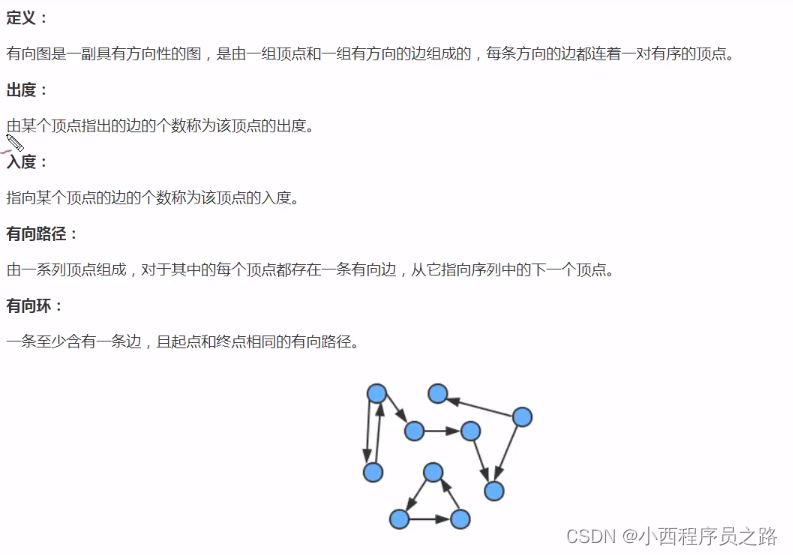
1.2有向图的实现 158

 

二、拓扑排序 159

基于有向图实现拓扑排序。

2.1检测有向图中的环 160

检测有向图环的目的：

有向图中存在环，就没办法进行拓扑排序了

2.1.1检测有向图中环API设计 160

 成员变量：onStack的原理：利用栈的思想进行操作的。如下所示：

2.1.2检测有向环实现 161

2.2基于深度优先顶点排序 162

2.2.1顶点排序API设计

2.2.2顶点排序实现的原理过程

文档P11

2.2.3顶点排序代码的实现及测试 162、163、164

三、加权无向图 165

 ​​​​​​​

3.1加权无向图边的表示---加权的边实现 166

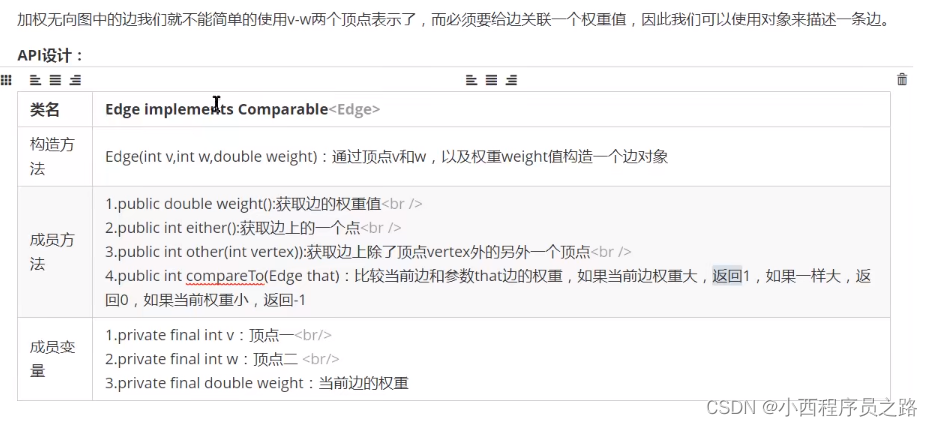
3.2加权无向图边的表示---无向图的实现 167

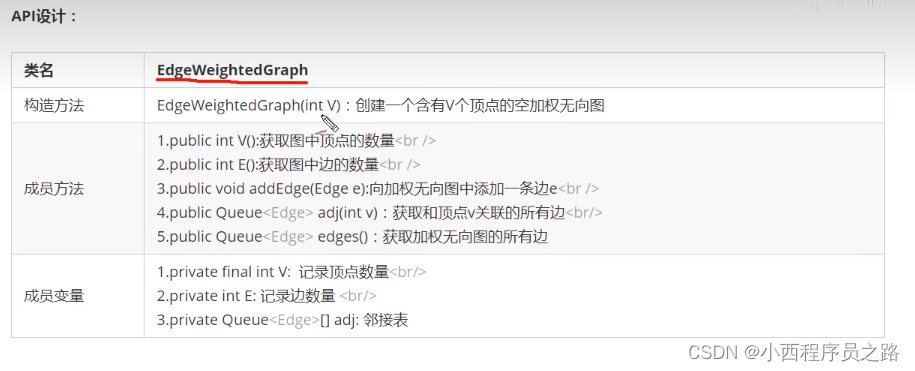
四、最小生成图 168

4.1最小生成树定义及相关约定 168

 

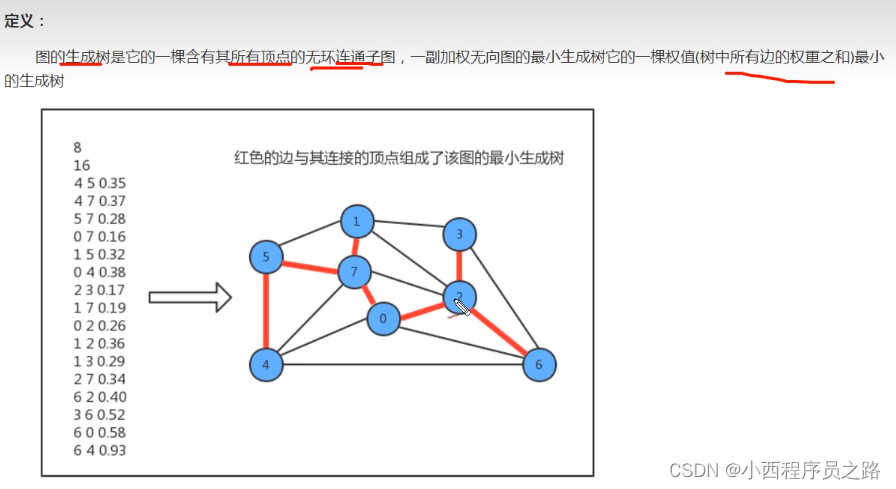
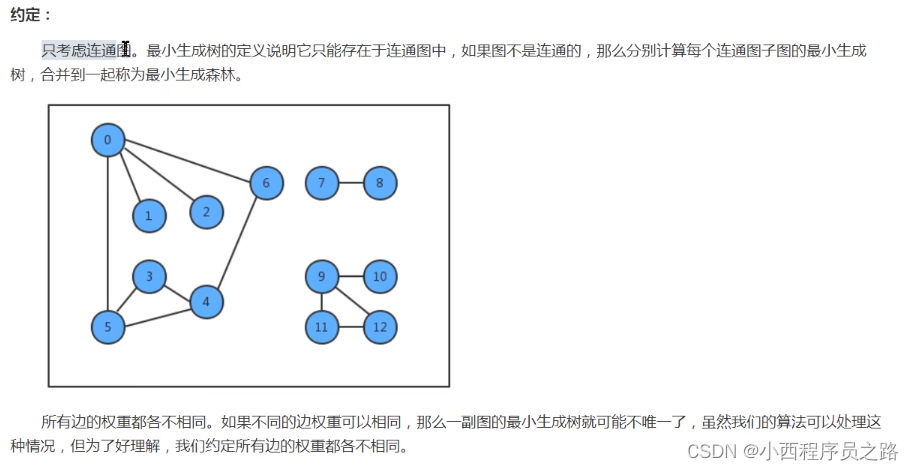
分别计算各个独立的连通图。这些组合在一起称为最小生成森林。

4.2最小生成树原理---切分定理 169

4.2.1树的性质

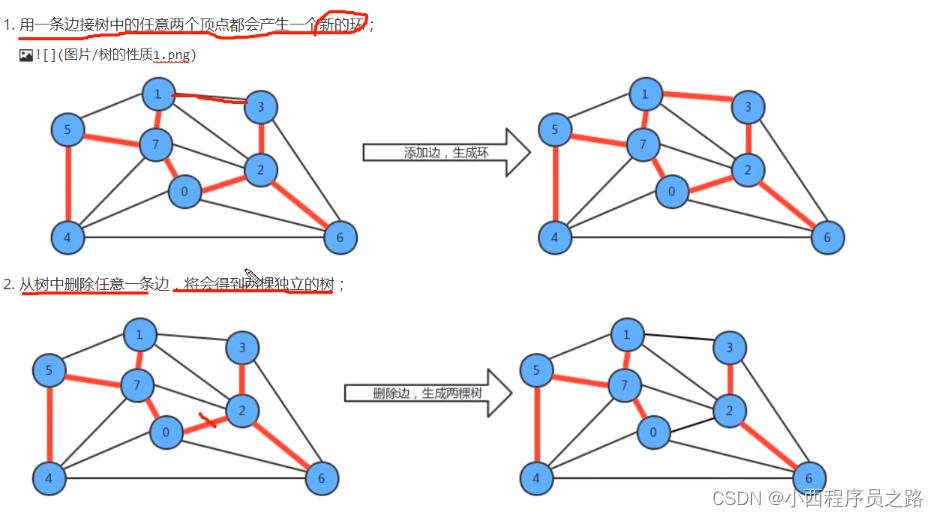
4.2.2切分定理

切分： 

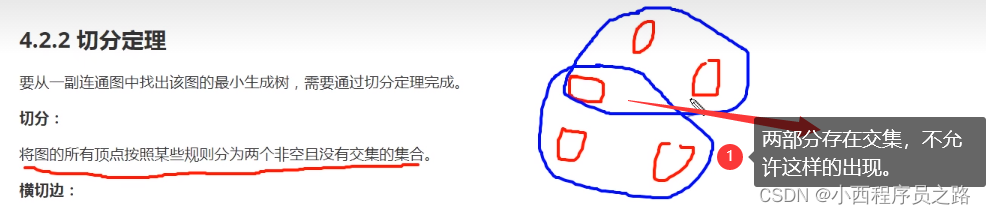
横切边：

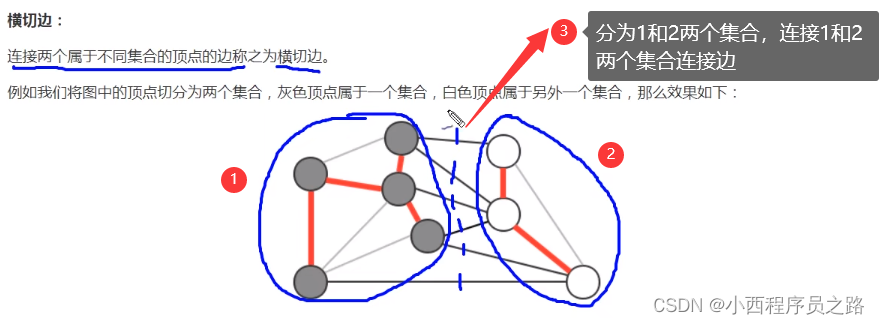
切分定理：

4.3贪心算法 170

基于切分定理实现的

步骤一：

步骤二：

步骤三：

 步骤四：

 步骤五：

 步骤六：

 步骤七：

 步骤八：直到所有的顶点都被连接起来，则说明查找完毕

 

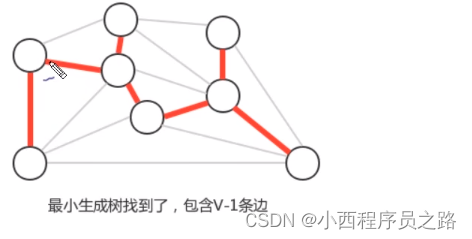
 贪心算法是基础：

求最小生成树的算法都是贪心算法的一种变形

4.4Prim算法 171

Prim算法实现的过程：

步骤一：

 ​​​​​​​步骤二：

 其他的部分依次类推，就可以找到所有的最小生成树了。

4.4.1Prim算法API设计

4.4.2Prim算法的实现原理 172  

参考文档P27

4.4.3Prim算法的代码实现及测试173、174、175

4.5kruskal算法 176

 ​​​​​​​

 

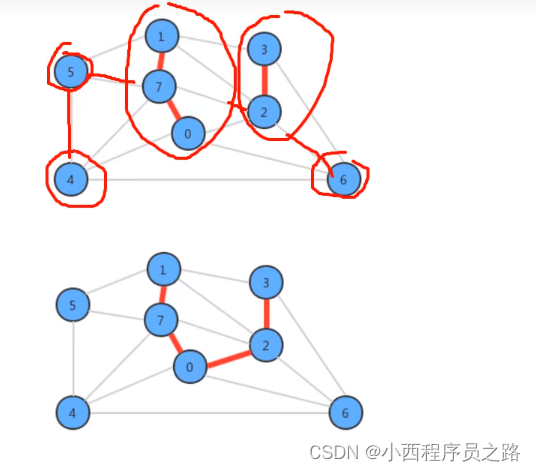
 是将森林进行连接

4.5.1kruskal算法API设计 

本部分使用了并查集 

4.5.2kruskal算法的实现原理 177

文档P32

4.5.3kruskal算法代码实现及测试 178、179

五、加权有向图 180

5.1加权有向图边的表示 180

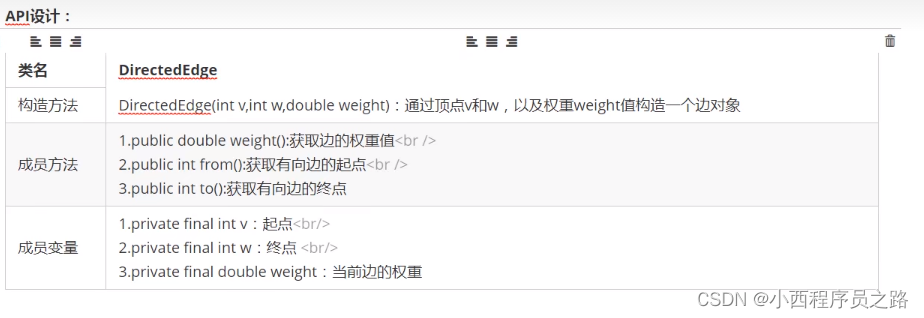
5.2加权有向图的实现 181

 

六、最短路径182

 ​​​​​​​

6.1最短路径定义及性质 182

这个不是最小生成树，最小生成树是所有的顶点都要连接起来，这个只是连接需要的两个顶点。

路径：可以是部分的连接

6.2最短路径树API设计 182

6.3松弛技术 183

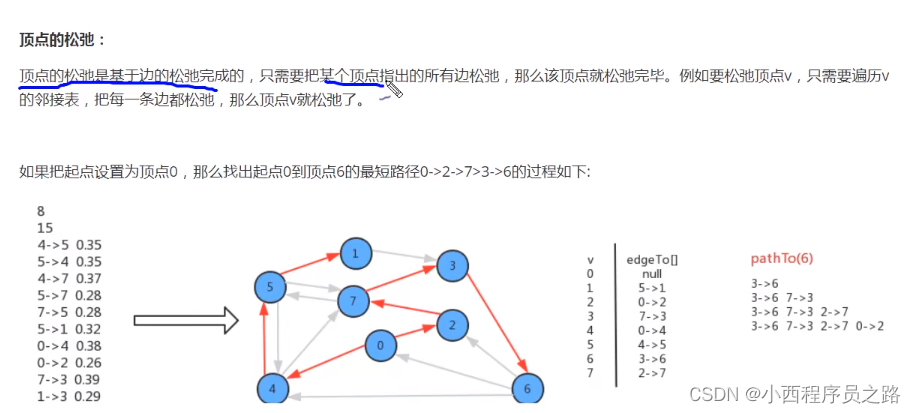
 边的松弛：

 顶点的松弛：

 

6.4Dijstra算法实现及测试 184、185、186