基于粒子群优化算法的边缘链接用于边缘检测（Matlab代码实现）

news2024/10/6 1:45:12

👨‍🎓个人主页：研学社的博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

💥1 概述

参考文献：

边缘检测是计算机视觉中的一个重要领域，检测噪声图像中的连续边缘是一个难题。自2009年以来，规范粒子群优化（CanPSO）一直用于边缘检测。尽管裸骨PSO（BBPSO）和完全知情粒子群（FIPS）作为PSO的两个知名版本，具有克服噪声的有趣功能，但它们从未应用于噪声图像中的边缘检测。本文在三个版本的PSO中实现了六种不同的静态拓扑和两种动态拓扑，并在基于PSO的边缘检测器中研究了它们在噪声图像中的影响。计算实验表明，在大多数情况下，采用环形拓扑的FIPS优于具有各种静态和动态拓扑的规范和裸骨PSO，并且对噪声的鲁棒性更强。

📚2 运行结果

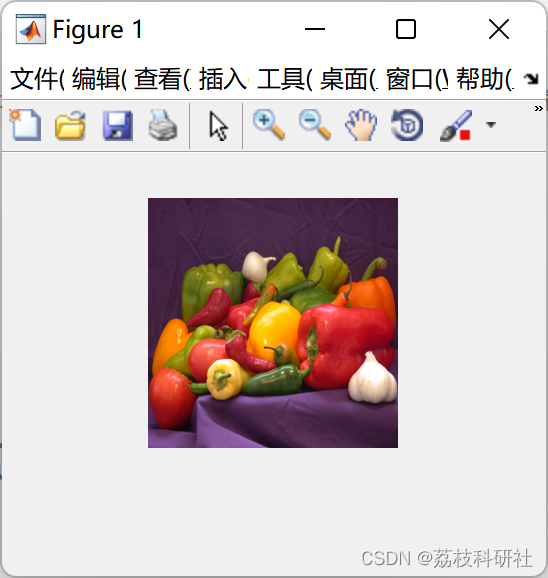
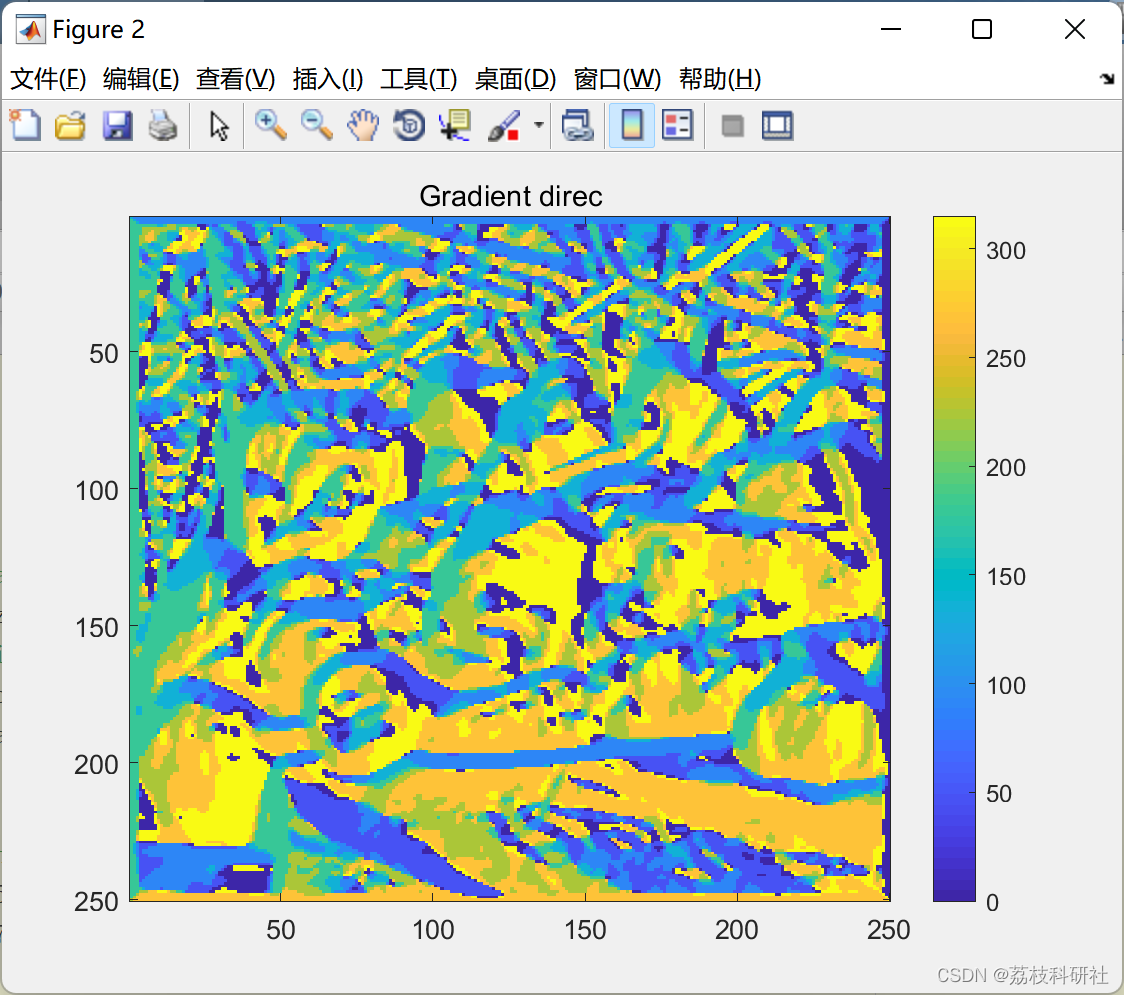
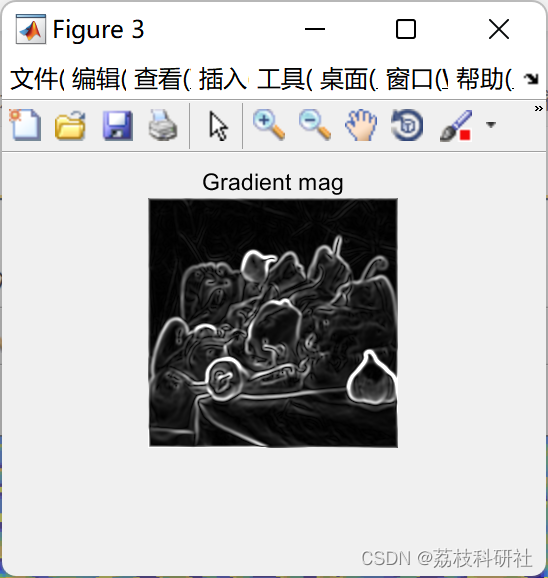
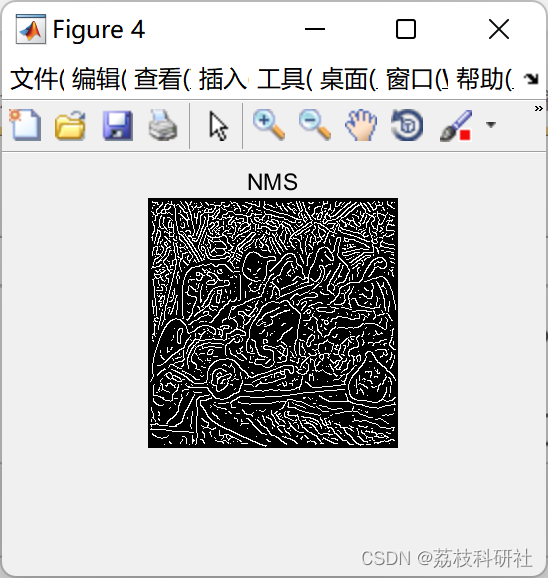
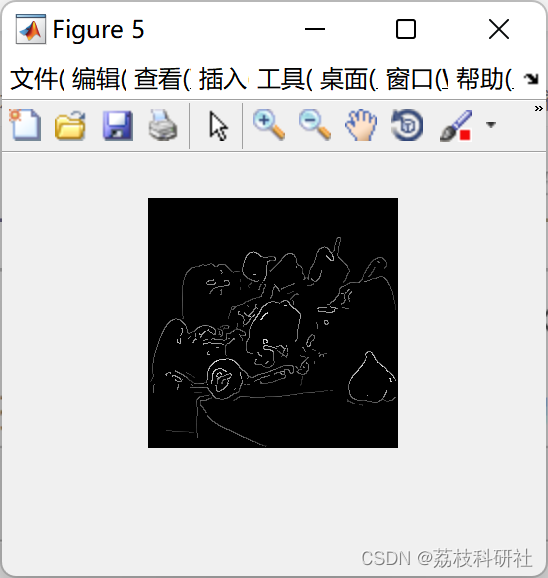
部分代码：

clear all;
close all;
clc;

%Input image
% img = imread ('coins.png');
img = imresize(imread ('peppers.png'),[250 250]);
%Show input image
figure, imshow(img);
img = rgb2gray(img);
img = double (img);

%Value for Thresholding
T_Low = 0.075;
T_High = 0.175;

%Gaussian Filter Coefficient
B = [2, 4, 5, 4, 2; 4, 9, 12, 9, 4;5, 12, 15, 12, 5;4, 9, 12, 9, 4;2, 4, 5, 4, 2 ];
B = 1/159.* B;

%Convolution of image by Gaussian Coefficient
A=conv2(img, B, 'same');

%Filter for horizontal and vertical direction
KGx = [-1, 0, 1; -2, 0, 2; -1, 0, 1];
KGy = [1, 2, 1; 0, 0, 0; -1, -2, -1];

%Convolution by image by horizontal and vertical filter
Filtered_X = conv2(A, KGx, 'same');
Filtered_Y = conv2(A, KGy, 'same');

%Calculate directions/orientations=atan2(Gx,Gy)
arah = atan2 (Filtered_Y, Filtered_X);
arah = arah*180/pi;

pan=size(A,1);
leb=size(A,2);

%Adjustment for negative directions, making all directions positive
for i=1:pan
for j=1:leb
if (arah(i,j)<0)
arah(i,j)=360+arah(i,j);
end;
end;
end;

arah2=zeros(pan, leb);

%Adjusting directions to nearest 0, 45, 90, or 135 degree
for i = 1 : pan
for j = 1 : leb
if ((arah(i, j) >= 0 ) && (arah(i, j) < 22.5) || (arah(i, j) >= 337.5) && (arah(i, j) <= 360))
arah2(i, j) = 0;
elseif ((arah(i, j) >= 22.5) && (arah(i, j) < 67.5))
arah2(i, j) = 45;
elseif ((arah(i, j) >= 67.5 && arah(i, j) < 112.5))
arah2(i, j) = 90;
elseif ((arah(i, j) >= 112.5 && arah(i, j) < 157.5))
arah2(i, j) = 135;
elseif ((arah(i, j) >= 157.5) && (arah(i, j) < 202.5))
arah2(i, j) = 180;
elseif ((arah(i, j) >= 202.5 && arah(i, j) < 247.5))
arah2(i, j) = 225;
elseif ((arah(i, j) >= 247.5 && arah(i, j) < 292.5))
arah2(i, j) = 270;
elseif ((arah(i, j) >= 292.5 && arah(i, j) < 337.5))
arah2(i, j) = 315;
end;
end;
end;

figure, imagesc(arah2); colorbar;title('Gradient direc')

%Calculate magnitude = sqrt(Gx^2+Gy^2)
magnitude = (Filtered_X.^2) + (Filtered_Y.^2);
magnitude2 = sqrt(magnitude);

figure, imshow(uint8(magnitude2));title('Gradient mag')
BW = zeros (pan, leb);

%Non-Maximum Supression
for i=2:pan-1 % mark the strong pixels as 1
for j=2:leb-1
if (arah2(i,j)==0 ||arah2(i,j)==180 )
BW(i,j) = (magnitude2(i,j) == max([magnitude2(i,j), magnitude2(i,j+1), magnitude2(i,j-1)]));
elseif (arah2(i,j)==45 ||arah2(i,j)==225)
BW(i,j) = (magnitude2(i,j) == max([magnitude2(i,j), magnitude2(i+1,j-1), magnitude2(i-1,j+1)]));
elseif (arah2(i,j)==90 ||arah2(i,j)==270)
BW(i,j) = (magnitude2(i,j) == max([magnitude2(i,j), magnitude2(i+1,j), magnitude2(i-1,j)]));
elseif (arah2(i,j)==135 ||arah2(i,j)==315)
BW(i,j) = (magnitude2(i,j) == max([magnitude2(i,j), magnitude2(i+1,j+1), magnitude2(i-1,j-1)]));
end;
end;
end;

BW = BW.*magnitude2; % get the marked pixel '1' values alone
figure, imshow(BW);title('NMS')

%Hysteresis Thresholding
T_Low = T_Low * max(max(BW));
T_High = T_High * max(max(BW));

h1 = @(cx) edgefitness(cx, img, ki, kj);
h2 = @(cx) curve_constraints(cx, ki, kj);
% ga_opts = gaoptimset(ga_opts,'TolFun', 1e-10,'StallGenLimit', 100, 'FitnessLimit', 1e-5,'display','iter');
ga_opts = gaoptimset( 'Generations', 30);
[cx, err_ga] = ga(h1,5,[],[],[],[],[1;1;0;0;0],[8;8;8;8;8],h2,[1 2 3 4 5],ga_opts); %atleast two neighbour per pixel
% 1 2 3
% 4 0 5
% 6 7 8

🌈3 Matlab代码实现

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]"Particle Swarm Optimisation for Edge Detection in Noisy Images, Mahdi Setayesh thesis" and "Effects of Static and Dynamic Topologies in Particle Swarm Optimisation for Edge Detection in Noisy Images"