阅读Abellán老师的Credal-C4.5时，发现好难。。。然后又额外补充了一些论文，终于稍微懂一点点了，所以记录如下。

credal set在DS theory的定义如下 [1]：

这句话的意思是（证据理论中的）credal set是一个概率的凸集，这里面的概率p(x)受到上界pl函数和下界bel函数的控制（约束），而p(x)是不定的，从而构成了一个集合。这个东西往外推广，得到如下形式：
$$l(x)\le p(x)\le u(x)$$
其中$l(x)$和$u(x)$是已知的下界和上界，这样的概率（泛函？）都称为是credal set。
那么credal set 是一个集合，这个东西怎么用起来呀？有的论文提出使得credal set的不确定信息量取得最大的模型是一个可用的模型，因此我们只要获得使得熵（这里可以是Shannon熵）取得最大的概率向量$p$，就可以了。想象一下，这是不是变成了一个有约束规划？目标方程是某种熵比如Shannon熵，约束条件是我刚刚给定的下界和上界。
关键概念总结： credal set，credal set的熵，credal set的最大熵，这些在近似的论文里很常见。

再回到credal decision tree。credal decision tree就是把信息论里面的香农熵全部换成了credal set的最大熵。其中credal set $K(Z)$和用的熵$H^{\ast }(K(Z))$是这么给的（其中$s$是一个参数，建议值1或2，当$s\in (0,2]$时优化很慢）：

所以credal decision tree就是用$H\ast (K(Z))$替换决策树中的香农熵，就可以了。不信的话可以看 [2] 的Example 2，公式如下：

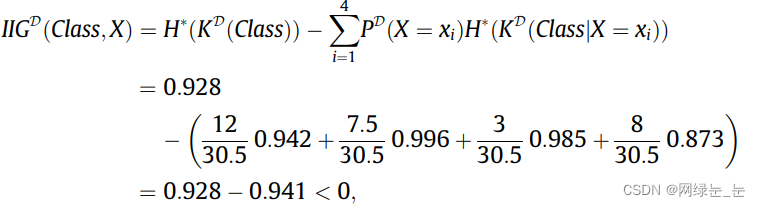
可以看到Imprecise Information Gain 是不是和传统的Information Gain 差不多？就是用credal set的最大熵换了下香农熵。

另外当$s\in (0,2]$时优化很慢，作者直接给出了$s=1$时使得credal set熵最大的$p$，用这个$p$直接算最大熵：

参考文献：
[1] Requirements for total uncertainty measures in Dempster–Shafer theory of evidence
[2] Credal-C4.5: Decision tree based on imprecise probabilities to classify noisy data