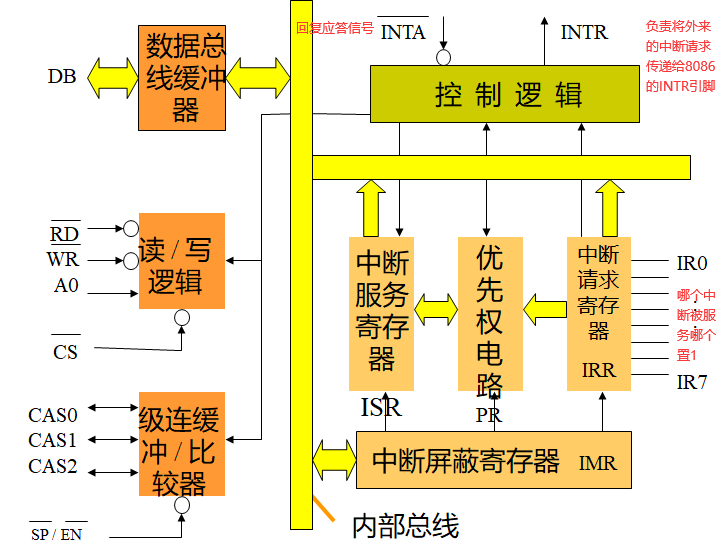
【paper】 TuckER: Tensor Factorization for Knowledge Graph Completion
【简介】 这篇文章是英国爱丁堡大学的研究者发表于 ICML 2019 上的文章,提出了 TuckER,是一个线性的张量分解模型,对表示三元组事实的二值张量做 Tucker 分解。
背景知识
本模型基于 1966 年 Tucker 提出的 Tucker decomposition,它将一个张量分解为一个 core tensor 和一组矩阵相乘的形式,可以被视为一种高阶 SVD 的形式,在矩阵是正交的和 core tensor 是“all-orthogonal(全正交)”的 special case 下。
文章声称 TuckER 是 fully expressive 的,这个词也在很多文章中见过,这里解释了它的含义:
对于给定的 golden triplet,一定有 embedding 各维度值的分配方法,使其与负样本分开。
TuckER 可以视为各种 bilinear model (RESCAL、DistMult、ComplEx、SimplE)的通用情况。
Related Work 中介绍了几大 bilinear 模型的方法和打分函数。
Tucker 分解:
一篇博客里介绍得很清楚,贴在这里好了:TuckER:Tensor Factorization for Knowledge Graph Completion_三石说的博客-CSDN博客_tensor factorization

模型
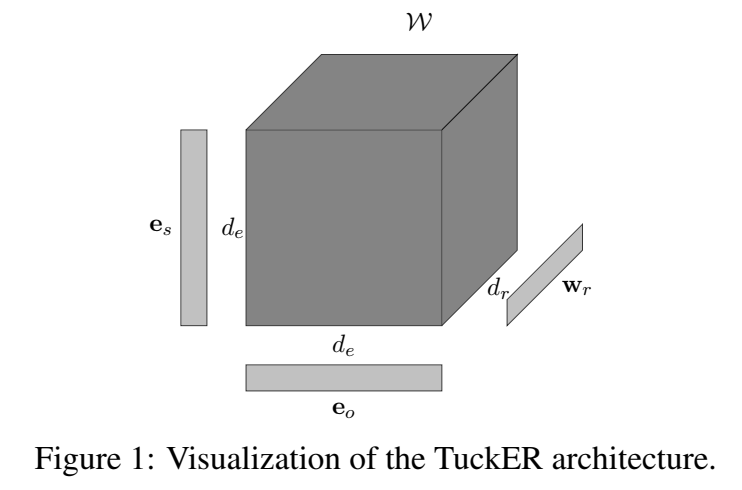
TuckER 对三元组的打分函数:
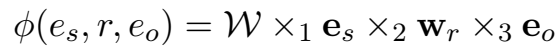
文章说,TuckER 的优势在于没有将所有的知识编码到 embedding 中,一些被储存在 core tensor 中,通过 multi-task learning 在实体和关系中共享。(不太理解。。。)
将上式计算出的三元组得分输入到 sigmoid 函数中,得到一个概率值,然后计算 loss(伯努利负 log-likelihood loss):
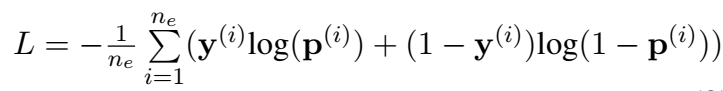
上面博客中的博主研读了代码:
在看代码之前,我认为这个评分函数是对整个三元组的评分,实际上代码中并不是这个意思。前向传播计算输出的是,一个矩阵,大小为(batch,len(entity)),输入的是一个batch的头实体和关系,相当于是在预测尾实体出现在每个位置的概率值。然后将这个概率值同目标位置组成的矩阵(正确位置为1)计算loss(可以理解为二分类问题)
理论分析
和 Rescal 的关系
Rescal 的打分函数是这样的:
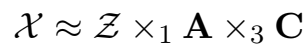
少了一个矩阵 B,关系矩阵就是 core tensor ZZ 的 slice。
表示非对称关系

对称关系训练出的矩阵是对称的,非对称关系的矩阵是非对称的。
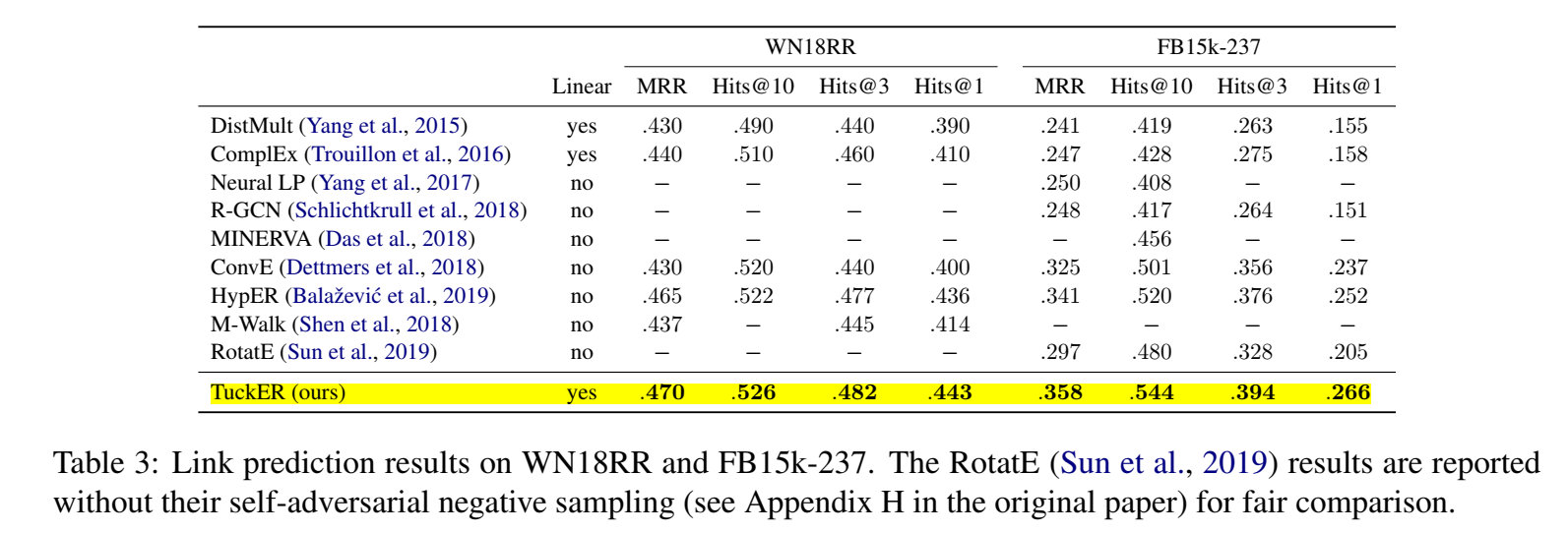
实验
在四个数据集(FB15k、FB15k-237、WN18、WN18RR)上进行了实验。
【code】 https://github.com/ibalazevic/TuckER
这个代码是用 PyTorch 实现的,看起来很简洁的样子,有时间的话真想好好学习一下,试着跑一下,but我没有。。。
双线性模型(六)(CrossE、RotatE、TuckER) - 胡萝不青菜 - 博客园