总结

• T1 模拟
• T2 单源最短路dijikstra
• T3 多源最短路floyd
• 

A - New Scheme

链接: A - New Scheme

1. 题目描述

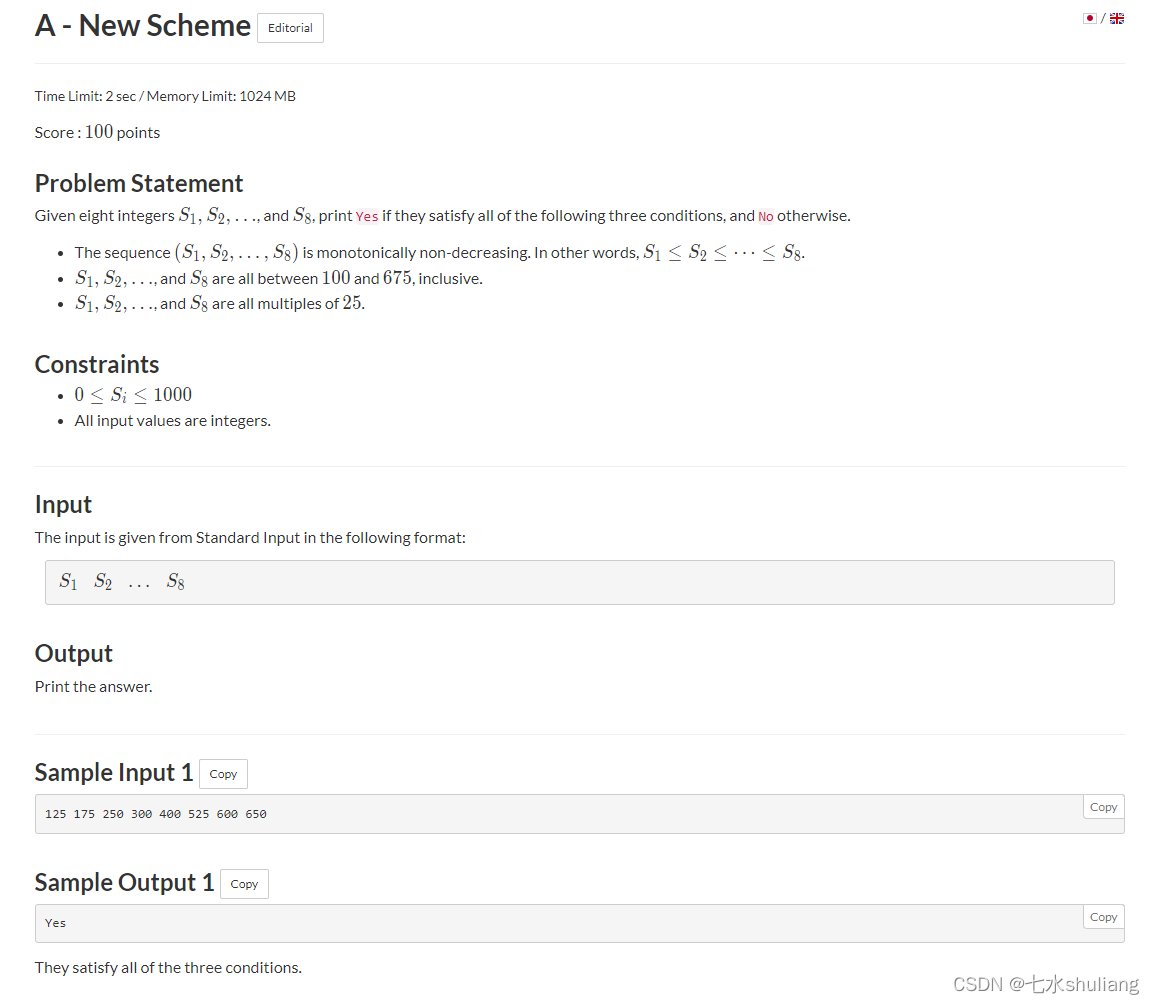
2. 思路分析

• 模拟。

3. 代码实现

# Problem: A - New Scheme
# Contest: AtCoder - AtCoder Beginner Contest 308
# URL: https://atcoder.jp/contests/abc308/tasks/abc308_a
# Memory Limit: 1024 MB
# Time Limit: 2000 ms

import sys
import random
from types import GeneratorType
import bisect
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from array import *
from functools import lru_cache, reduce
from heapq import *
from math import sqrt, gcd, inf

if sys.version >= '3.8':  # ACW没有comb
    from math import comb

RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
# print = lambda d: sys.stdout.write(str(d) + "\n")  # 打开可以快写，但是无法使用print(*ans,sep=' ')这种语法,需要print(' '.join(map(str, p)))，确实会快。

DIRS = [(0, 1), (1, 0), (0, -1), (-1, 0)]  # 右下左上
DIRS8 = [(0, 1), (1, 1), (1, 0), (1, -1), (0, -1), (-1, -1), (-1, 0),
         (-1, 1)]  # →↘↓↙←↖↑↗
RANDOM = random.randrange(2 ** 62)
MOD = 10 ** 9 + 7
# MOD = 998244353
PROBLEM = """给8个数字，检测是否同时满足下边3个性质
1. 数列单调不降
2. 每个数都在100~675之间
3. 每个数都是25的倍数
"""


def lower_bound(lo: int, hi: int, key):
    """由于3.10才能用key参数，因此自己实现一个。
    :param lo: 二分的左边界(闭区间)
    :param hi: 二分的右边界(闭区间)
    :param key: key(mid)判断当前枚举的mid是否应该划分到右半部分。
    :return: 右半部分第一个位置。若不存在True则返回hi+1。
    虽然实现是开区间写法，但为了思考简单，接口以[左闭,右闭]方式放出。
    """
    lo -= 1  # 开区间(lo,hi)
    hi += 1
    while lo + 1 < hi:  # 区间不为空
        mid = (lo + hi) >> 1  # py不担心溢出，实测py自己不会优化除2，手动写右移
        if key(mid):  # is_right则右边界向里移动，目标区间剩余(lo,mid)
            hi = mid
        else:  # is_left则左边界向里移动，剩余(mid,hi)
            lo = mid
    return hi


def bootstrap(f, stack=[]):
    def wrappedfunc(*args, **kwargs):
        if stack:
            return f(*args, **kwargs)
        else:
            to = f(*args, **kwargs)
            while True:
                if type(to) is GeneratorType:
                    stack.append(to)
                    to = next(to)
                else:
                    stack.pop()
                    if not stack:
                        break
                    to = stack[-1].send(to)
            return to

    return wrappedfunc


#       ms
def solve():
    a = RILST()
    for i in range(1, 8):
        if a[i - 1] > a[i]:
            return print('No')
    for i, v in enumerate(a):
        if v % 25:
            return print('No')
        if not 100 <= v <= 675:
            return print('No')
    print('Yes')


if __name__ == '__main__':
    t = 0
    if t:
        t, = RI()
        for _ in range(t):
            solve()
    else:
        solve()

B - Default Price

链接: B - Default Price

1. 题目描述

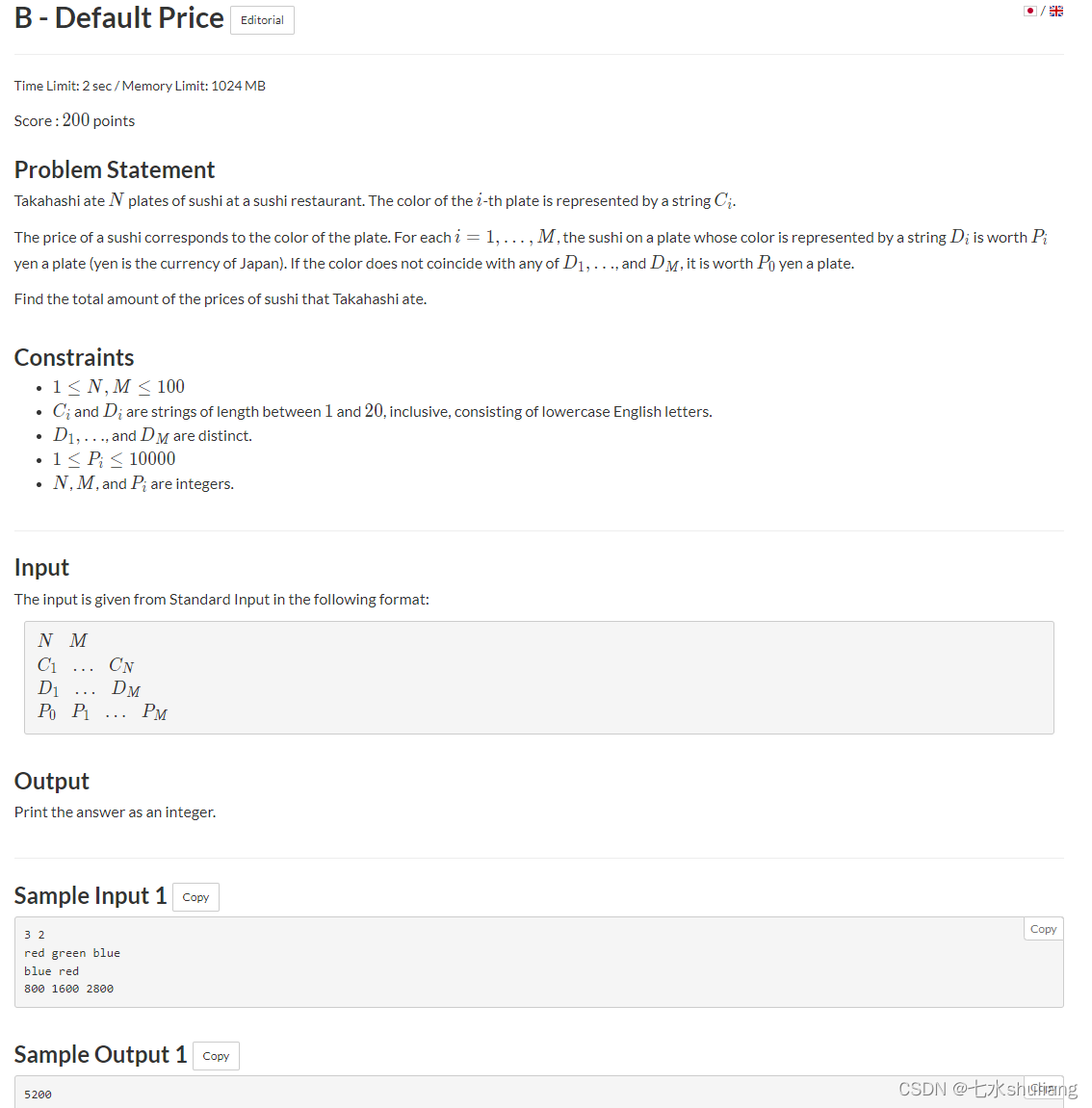
2. 思路分析

3. 代码实现

PROBLEM = """给n盘寿司，和每盘寿司的颜色。
给出m种颜色对应的价格，若吃的寿司没有给出，则价格是p[0].
问一共花了多少钱。
"""
"""哈希表模拟"""


#       ms
def solve():
    n, m = RI()
    cs = list(RS())
    ds = list(RS())
    p0, *ps = RI()
    dd = {d: p for d, p in zip(ds, ps)}
    print(sum(dd.get(c, p0) for c in cs))

C - Standings

链接: C - Standings

1. 题目描述

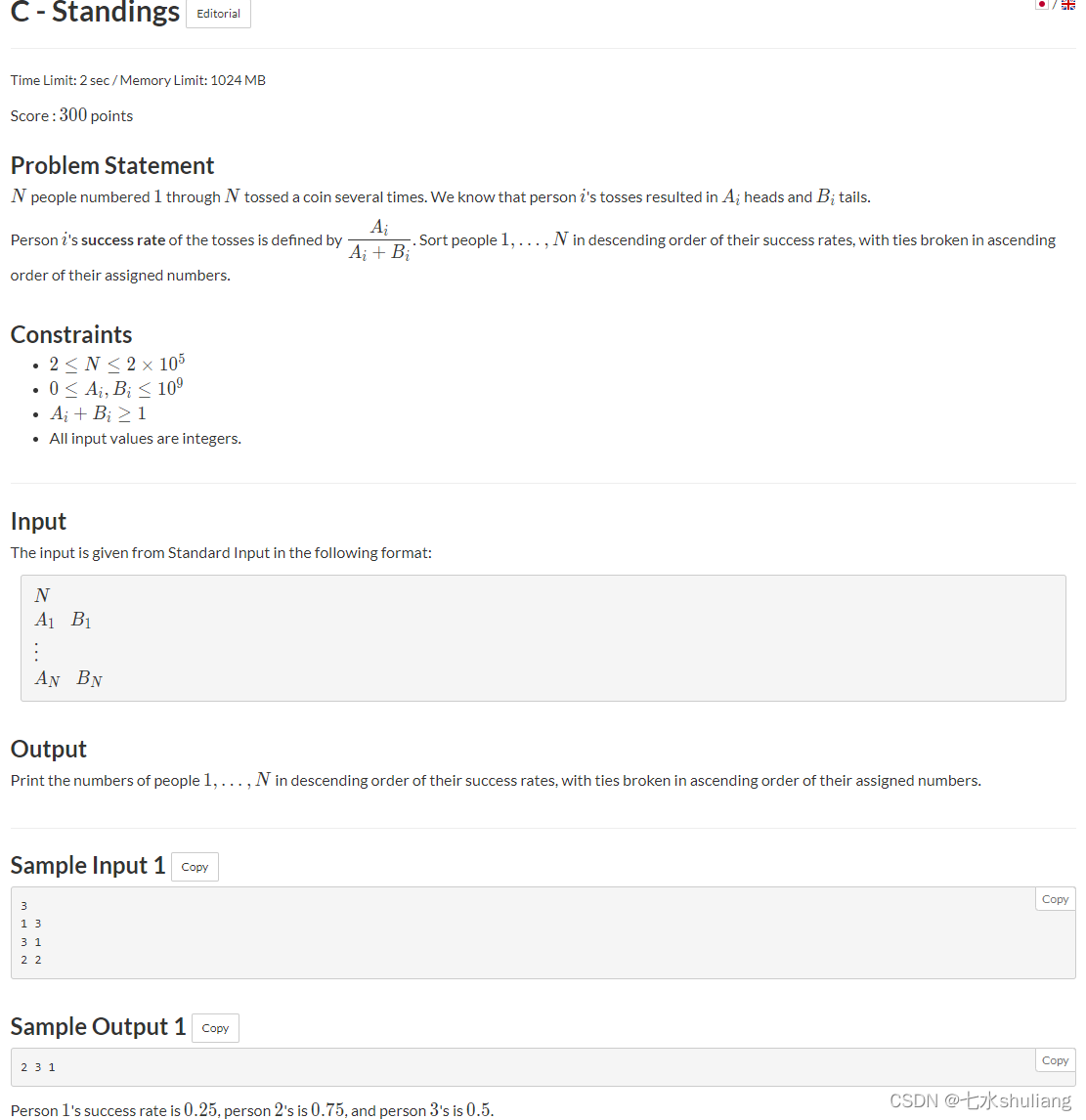
2. 思路分析

• 这题主要是用key=lambda自定义key方式会wa4组，卡精度了。必须转化成乘法防止丢精度。

3. 代码实现

PROBLEM = """给出每个人投硬币正面和反面的次数，定义命中率为a/(a+b)，
要求按命中率降序，若相同，则按序号升序。
"""
"""其实就是自定义排序，但py的自定义key写法涉及到浮点数，这题会卡。
因此要自定义比较器：`key=cmp_to_key(comp)`.
实现时return 小值-大值。
具体参考代码
"""


#       ms
def solve():
    n, = RI()
    a = []
    for i in range(1, n + 1):
        x, y = RI()
        a.append((x, y, i))

    def comp(t1, t2):
        if t1[0] * (t2[0] + t2[1]) == t2[0] * (t1[0] + t1[1]):
            return t1[2] - t2[2]
        return -t1[0] * (t2[0] + t2[1]) + t2[0] * (t1[0] + t1[1])

    a.sort(key=cmp_to_key(comp))
    print(*[y for _, _, y in a])

D - Snuke Maze

链接: D - Snuke Maze

1. 题目描述

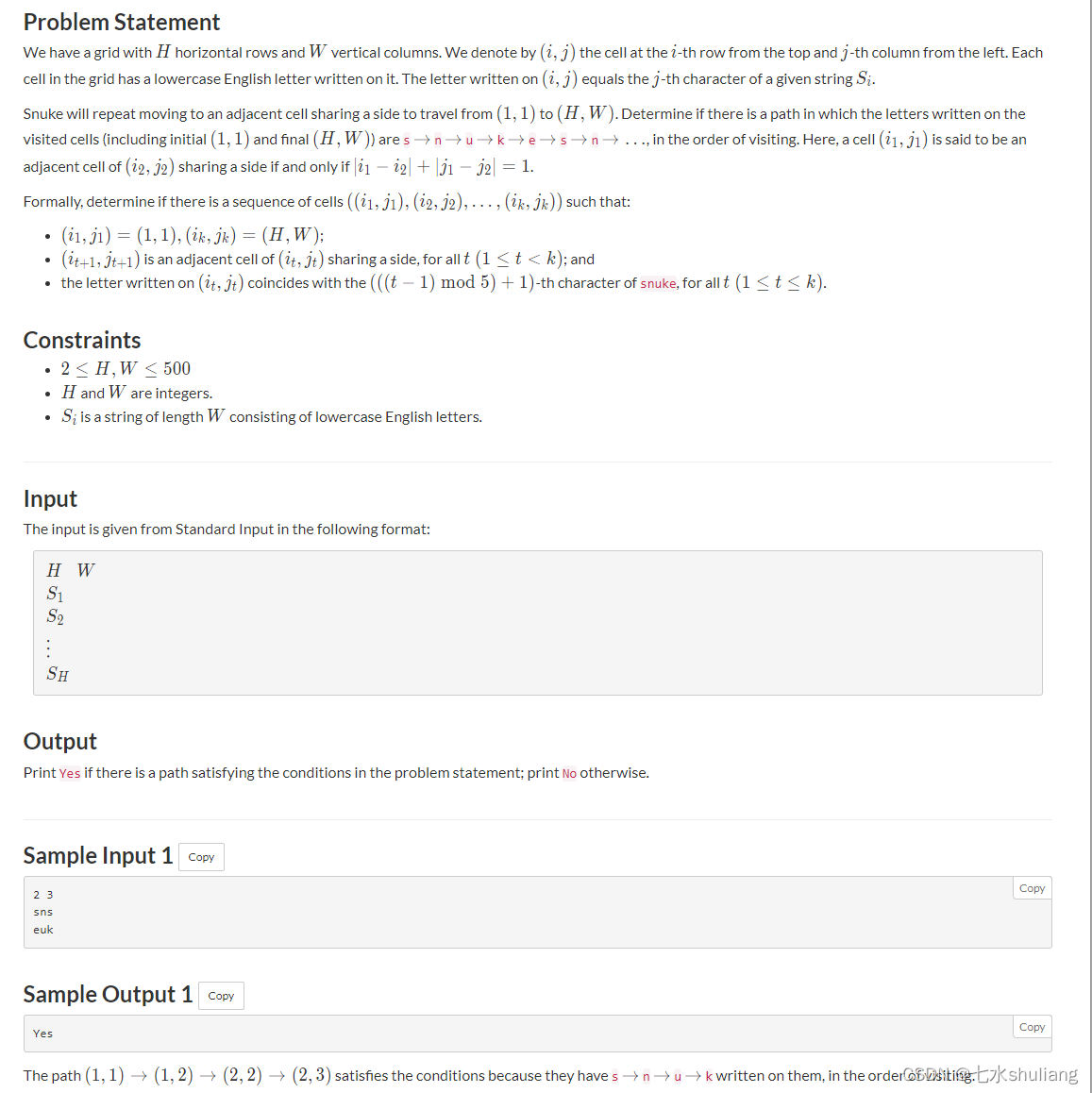
2. 思路分析

• 主要是在dp和bfs之间选择。

3. 代码实现

PROBLEM = """给出h行w列矩阵，每个位置是字母。
玩家从左上角走到右下角，沿路的字母组成的路径必须是'snuke'循环，问是否可以到达右下角。
"""
"""
显然转移的方向是按字母的，但是会循环。还是BFS比较方便，直接从左上角出发，向下一个字母转移即可。"""



#       ms
def solve():
    h, w = RI()
    g = []
    for _ in range(h):
        s, = RS()
        g.append(s)
    t = 'snuke'
    # if g[0][0] != 's' or g[-1][-1] != t[(h+w-1)%5]:
    if g[0][0] != 's':
        return print('No')
    dd = {}
    for i in range(1, len(t)):
        dd[t[i - 1]] = t[i]
    dd[t[-1]] = t[0]
    vis = [[0] * w for _ in range(h)]
    vis[0][0] = 1
    q = deque([(0, 0)])
    while q:
        x, y = q.popleft()
        c = g[x][y]
        d = dd[c]
        for dx, dy in DIRS:
            a, b = x + dx, y + dy
            if 0 <= a < h and 0 <= b < w and not vis[a][b] and g[a][b] == d:
                if a == h-1 and b == w-1:
                    return print('Yes')
                vis[a][b] = 1
                q.append((a, b))
    # print(vis)
    print('No')

E - MEX

链接: E - MEX

1. 题目描述

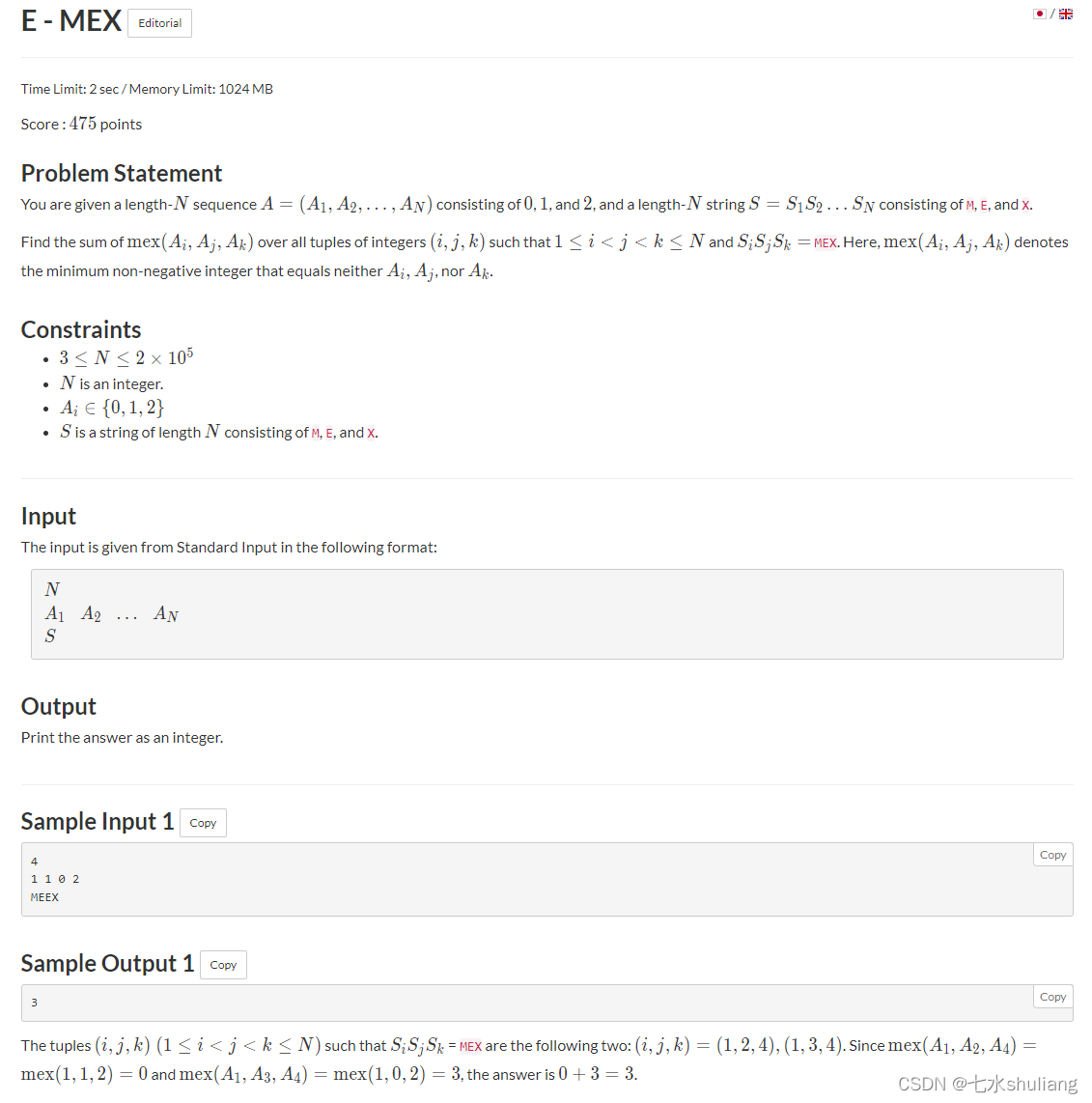
2. 思路分析

• 需要熟悉mex的定义和计算方式，知道复杂度，才敢继续。

3. 代码实现

PROBLEM = """给出长为n的数列a，仅包含012
给出长为n的字符串s，仅包含'm''e''x'。
找到所有s中的mex三元组下标，对应的a中的三个数组成的集合，求mex，最后sum。
"""
"""由于三元组只含012因此一定求mex可以暴力最多操作4次。
mex一定从me转移而来才有效，me一定从m转移而来才有效。
而这些字母对应数字是有限的，可以用哈希表计数即可。
"""


def mex(s):
    for i in count(0):
        if i not in s:
            return i


#       ms
def solve():
    n, = RI()
    a = RILST()
    s, = RS()
    ans = 0
    m, me, x = Counter(), Counter(), Counter()
    i = 0
    for x, c in zip(a, s):
        if c == 'M':
            m[x] += 1
        elif c == 'E':
            for k, v in m.items():
                me[(k, x)] += v
        else:
            for k, v in me.items():
                s = set(k)
                s.add(x)

                ans += mex(s) * v
        i += 1
    print(ans)

F - Vouchers

链接: F - Vouchers

1. 题目描述

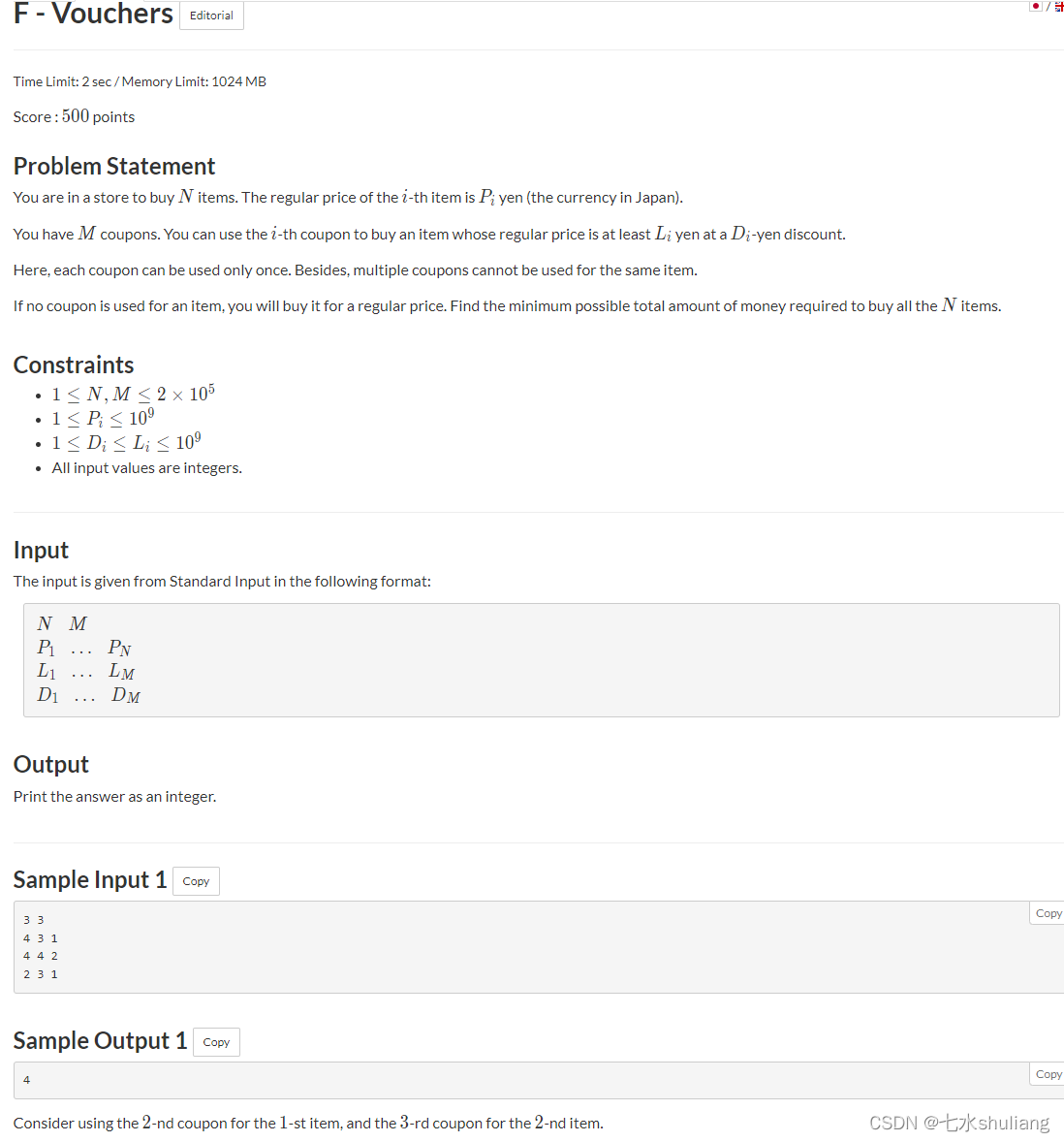
2. 思路分析

• 一眼贪心，但要考虑从大头优先匹配还是小头。

3. 代码实现

PROBLEM = """你要买n个物品，价格分别是pi.
你有m张满L减D的优惠券，每张券只能用一次。
问最少花多少钱可以买完这n个物品。
"""
"""贪心。
考虑双指针贪心，从大头开始还是小头。
发现大头不好贪。
从价格低物品开始买，考虑它能用哪张优惠券，选减得最多那个。这张券给更贵的不如给它用。
那么双指针+堆维护当前能用的券里最优那张即可。
"""


#  贪     ms
def solve():
    n, m = RI()
    p = RILST()
    l = RILST()
    d = RILST()
    p.sort()
    a = sorted(zip(l, d))
    h = []
    j = 0
    ans = 0
    for v in p:
        while j < m and a[j][0] <= v:
            heappush(h, -a[j][1])
            j += 1
        ans += v
        if h:
            ans += heappop(h)
    print(ans)

G - Minimum Xor Pair Query

链接: G - Minimum Xor Pair Query

1. 题目描述

2. 思路分析

• 结论题。
• 我们常说异或运算同时具有加法和减法的一些性质。
• 这里是和减法性质一致：
  • 一个集合里异或值最小的两个数，一定是相邻的。
• 因此排序后we

3. 代码实现

PROBLEM = """你有三个操作：
1.向集合里添加一个数x
2.从集合里删除一个数x
3.询问集合里两个数异或，最小是几。
"""
"""结论题：集合里最小两个数异或，一定是相邻两个数异或 """


class CuteSortedList:
    def __init__(self, iterable=[], _load=200):
        """Initialize sorted list instance."""
        values = sorted(iterable)
        self._len = _len = len(values)
        self._load = _load
        self._lists = _lists = [values[i:i + _load] for i in range(0, _len, _load)]
        self._list_lens = [len(_list) for _list in _lists]
        self._mins = [_list[0] for _list in _lists]
        self._fen_tree = []
        self._rebuild = True

    def _fen_build(self):
        """Build a fenwick tree instance."""
        self._fen_tree[:] = self._list_lens
        _fen_tree = self._fen_tree
        for i in range(len(_fen_tree)):
            if i | i + 1 < len(_fen_tree):
                _fen_tree[i | i + 1] += _fen_tree[i]
        self._rebuild = False

    def _fen_update(self, index, value):
        """Update `fen_tree[index] += value`."""
        if not self._rebuild:
            _fen_tree = self._fen_tree
            while index < len(_fen_tree):
                _fen_tree[index] += value
                index |= index + 1

    def _fen_query(self, end):
        """Return `sum(_fen_tree[:end])`."""
        if self._rebuild:
            self._fen_build()

        _fen_tree = self._fen_tree
        x = 0
        while end:
            x += _fen_tree[end - 1]
            end &= end - 1
        return x

    def _fen_findkth(self, k):
        """Return a pair of (the largest `idx` such that `sum(_fen_tree[:idx]) <= k`, `k - sum(_fen_tree[:idx])`)."""
        _list_lens = self._list_lens
        if k < _list_lens[0]:
            return 0, k
        if k >= self._len - _list_lens[-1]:
            return len(_list_lens) - 1, k + _list_lens[-1] - self._len
        if self._rebuild:
            self._fen_build()

        _fen_tree = self._fen_tree
        idx = -1
        for d in reversed(range(len(_fen_tree).bit_length())):
            right_idx = idx + (1 << d)
            if right_idx < len(_fen_tree) and k >= _fen_tree[right_idx]:
                idx = right_idx
                k -= _fen_tree[idx]
        return idx + 1, k

    def _delete(self, pos, idx):
        """Delete value at the given `(pos, idx)`."""
        _lists = self._lists
        _mins = self._mins
        _list_lens = self._list_lens

        self._len -= 1
        self._fen_update(pos, -1)
        del _lists[pos][idx]
        _list_lens[pos] -= 1

        if _list_lens[pos]:
            _mins[pos] = _lists[pos][0]
        else:
            del _lists[pos]
            del _list_lens[pos]
            del _mins[pos]
            self._rebuild = True

    def _loc_left(self, value):
        """Return an index pair that corresponds to the first position of `value` in the sorted list."""
        if not self._len:
            return 0, 0

        _lists = self._lists
        _mins = self._mins

        lo, pos = -1, len(_lists) - 1
        while lo + 1 < pos:
            mi = (lo + pos) >> 1
            if value <= _mins[mi]:
                pos = mi
            else:
                lo = mi

        if pos and value <= _lists[pos - 1][-1]:
            pos -= 1

        _list = _lists[pos]
        lo, idx = -1, len(_list)
        while lo + 1 < idx:
            mi = (lo + idx) >> 1
            if value <= _list[mi]:
                idx = mi
            else:
                lo = mi

        return pos, idx

    def _loc_right(self, value):
        """Return an index pair that corresponds to the last position of `value` in the sorted list."""
        if not self._len:
            return 0, 0

        _lists = self._lists
        _mins = self._mins

        pos, hi = 0, len(_lists)
        while pos + 1 < hi:
            mi = (pos + hi) >> 1
            if value < _mins[mi]:
                hi = mi
            else:
                pos = mi

        _list = _lists[pos]
        lo, idx = -1, len(_list)
        while lo + 1 < idx:
            mi = (lo + idx) >> 1
            if value < _list[mi]:
                idx = mi
            else:
                lo = mi

        return pos, idx

    def add(self, value):
        """Add `value` to sorted list."""
        _load = self._load
        _lists = self._lists
        _mins = self._mins
        _list_lens = self._list_lens

        self._len += 1
        if _lists:
            pos, idx = self._loc_right(value)
            self._fen_update(pos, 1)
            _list = _lists[pos]
            _list.insert(idx, value)
            _list_lens[pos] += 1
            _mins[pos] = _list[0]
            if _load + _load < len(_list):
                _lists.insert(pos + 1, _list[_load:])
                _list_lens.insert(pos + 1, len(_list) - _load)
                _mins.insert(pos + 1, _list[_load])
                _list_lens[pos] = _load
                del _list[_load:]
                self._rebuild = True
        else:
            _lists.append([value])
            _mins.append(value)
            _list_lens.append(1)
            self._rebuild = True

    def discard(self, value):
        """Remove `value` from sorted list if it is a member."""
        _lists = self._lists
        if _lists:
            pos, idx = self._loc_right(value)
            if idx and _lists[pos][idx - 1] == value:
                self._delete(pos, idx - 1)

    def remove(self, value):
        """Remove `value` from sorted list; `value` must be a member."""
        _len = self._len
        self.discard(value)
        if _len == self._len:
            raise ValueError('{0!r} not in list'.format(value))

    def pop(self, index=-1):
        """Remove and return value at `index` in sorted list."""
        pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
        value = self._lists[pos][idx]
        self._delete(pos, idx)
        return value

    def bisect_left(self, value):
        """Return the first index to insert `value` in the sorted list."""
        pos, idx = self._loc_left(value)
        return self._fen_query(pos) + idx

    def bisect_right(self, value):
        """Return the last index to insert `value` in the sorted list."""
        pos, idx = self._loc_right(value)
        return self._fen_query(pos) + idx

    def count(self, value):
        """Return number of occurrences of `value` in the sorted list."""
        return self.bisect_right(value) - self.bisect_left(value)

    def __len__(self):
        """Return the size of the sorted list."""
        return self._len

    # def __getitem__(self, index):
    #     """Lookup value at `index` in sorted list."""
    #     pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
    #     return self._lists[pos][idx]
    def __getitem__(self, index):
        """Lookup value at `index` in sorted list."""
        if isinstance(index, slice):
            _lists = self._lists
            start, stop, step = index.indices(self._len)
            if step == 1 and start < stop:  # 如果是正向的步进1，找到起起止点，然后把中间的拼接起来即可
                if start == 0 and stop == self._len:  # 全部
                    return reduce(iadd, self._lists, [])
                start_pos, start_idx = self._fen_findkth(start)
                start_list = _lists[start_pos]
                stop_idx = start_idx + stop - start

                # Small slice optimization: start index and stop index are
                # within the start list.

                if len(start_list) >= stop_idx:
                    return start_list[start_idx:stop_idx]

                if stop == self._len:
                    stop_pos = len(_lists) - 1
                    stop_idx = len(_lists[stop_pos])
                else:
                    stop_pos, stop_idx = self._fen_findkth(stop)

                prefix = _lists[start_pos][start_idx:]
                middle = _lists[(start_pos + 1):stop_pos]
                result = reduce(iadd, middle, prefix)
                result += _lists[stop_pos][:stop_idx]
                return result
            if step == -1 and start > stop:  # 如果是负向的步进1，直接翻转调用自己再翻转即可
                result = self.__getitem__(slice(stop + 1, start + 1))
                result.reverse()
                return result

            indices = range(start, stop, step)  # 若不是步进1，只好一个一个取
            return list(self.__getitem__(index) for index in indices)

        else:
            pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
            return self._lists[pos][idx]

    def __delitem__(self, index):
        """Remove value at `index` from sorted list."""
        pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
        self._delete(pos, idx)

    def __contains__(self, value):
        """Return true if `value` is an element of the sorted list."""
        _lists = self._lists
        if _lists:
            pos, idx = self._loc_left(value)
            return idx < len(_lists[pos]) and _lists[pos][idx] == value
        return False

    def __iter__(self):
        """Return an iterator over the sorted list."""
        return (value for _list in self._lists for value in _list)

    def __reversed__(self):
        """Return a reverse iterator over the sorted list."""
        return (value for _list in reversed(self._lists) for value in reversed(_list))

    def __repr__(self):
        """Return string representation of sorted list."""
        return 'SortedList({0})'.format(list(self))




#       ms
def solve():
    n , = RI()
    ans = CuteSortedList()
    a = CuteSortedList()
    for _ in range(n):
        s = RILST()

        if s[0] == 1:
            x = s[1]
            t = a.bisect_left(x)
            if t and t < len(a):
                ans.remove(a[t] ^ a[t - 1])
            if t:
                ans.add(a[t - 1] ^ x)
            if t < len(a):
                ans.add(a[t] ^ x)
            a.add(x)
        elif s[0] == 2:
            x = s[1]
            t = a.bisect_left(x)
            if t:
                ans.remove(a[t - 1] ^ x)
            if t < len(a) - 1:
                ans.remove(a[t + 1] ^ x)
            if t and t < len(a) - 1:
                ans.add(a[t + 1] ^ a[t - 1])
            a.remove(x)
        else:
            print(ans[0])

六、参考链接

• 无