数据结构之串

news2024/9/17 8:20:12

1.串的基本概念

• 一个串是由n（n≥0）个字符组成的有限序列，记为s=“s0s1 ⋯ sn-1”，其
中，s是串名，双引号括起来的字符序列s0s1 ⋯ sn-1是串值。
• 一个字符在串中的位置称为该字符在串中的序号，约定串第一个字符
的序号为0。
• 由串s中任意连续字符组成的子序列称为s的子串，s称为主串。空串是任意串的子串；任意串都是它自身的子串；除自身外，串的其他子串称为其真子串。
• 子串的序号是指该子串首字符在主串中的序号。
• 两个串相等是指，串长度相同且对应位置上的字符也相同。

2.串的存储结构

（1）串的顺序存储结构
采用字符数组将串中的字符序列依次存储在数组的相邻单元中。
在这里插入图片描述
顺序串具有随机存取特性，存取指定位置字符的时间复杂度为O(1)；
缺点是插入、删除时需要移动数据元素，平均移动数据量是串长度
的一半，插入、删除操作的时间复杂度为O(n)。
（2）串的链式存储结构
串的链式存储结构有单字符链表和块链表两种，如下图所示。
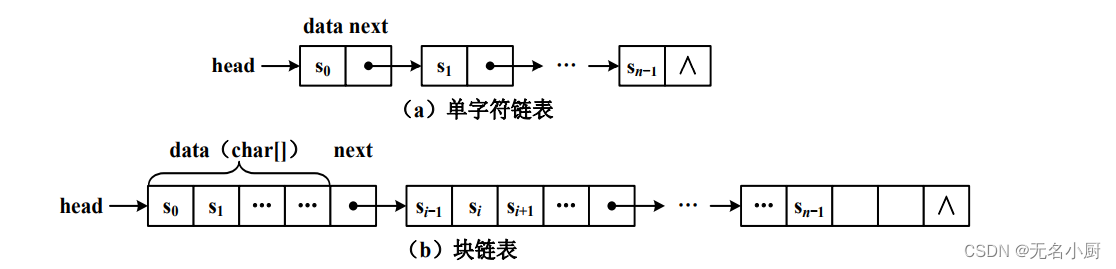
在这里插入图片描述
链式存储的串，存取指定位置字符的时间复杂度为O(n)；
单字符链表虽然插入删除操作不需要移动数据元素，但占用存储空间太
多；块链表的插入和删除操作需要移动元素，效率较低。

3.串的模式匹配

定义：设有两个串目标串target和模式串pattern，在目标串target中查找
与模式串pattern相等的一个子串并确定该子串位置的操作称为串的模式
匹配（Pattern Matching）。
匹配结果有两种：如果target中存在与pattern相等的子串，则匹配成
功，获得该子串在target中的位置；否则匹配失败，给出失败信息。

4.模式匹配算法

（1）Brute-Force（BF）算法
BF算法的基本思想是蛮力匹配，即从目标串target的每一个字符开始依次与模式串pattern的字符进行比较。
（2）KMP算法
KMP算法是一种无回溯的模式匹配算法，它改进了BF算法，目标串不回溯。

5.BF算法描述与实现

 public int indexOf(MyString pattern, int begin) {
        int n = this.length(), m = pattern.length();
        if (begin < 0) //对begin容错，若begin<0，从0开始
            begin = 0;
        if (n == 0 || n < m || begin >= n) //若目标串空、较短或begin越界，不需比较
            return -1;
        int i = begin, j = 0; //i、j分别为目标串和模式串当前字符下标
        int count = 0; //记载比较次数
        while (i < n && j < m) {
            count++;
            if (this.charAt(i) == pattern.charAt(j)) //若当前两字符相等，则继续比较后续字符
            {
                i++;
                j++;
            } else //否则i、j回溯，进行下次匹配
            {
                i = i - j + 1; //目标串下标i，退回到下个匹配子串序号
                j = 0; //模式串下标j，退回到0
                if (i > n - m) //若目标串剩余子串的长度<m，不再比较
                    break;
            }
        }
    }

5.1BF算法算法分析

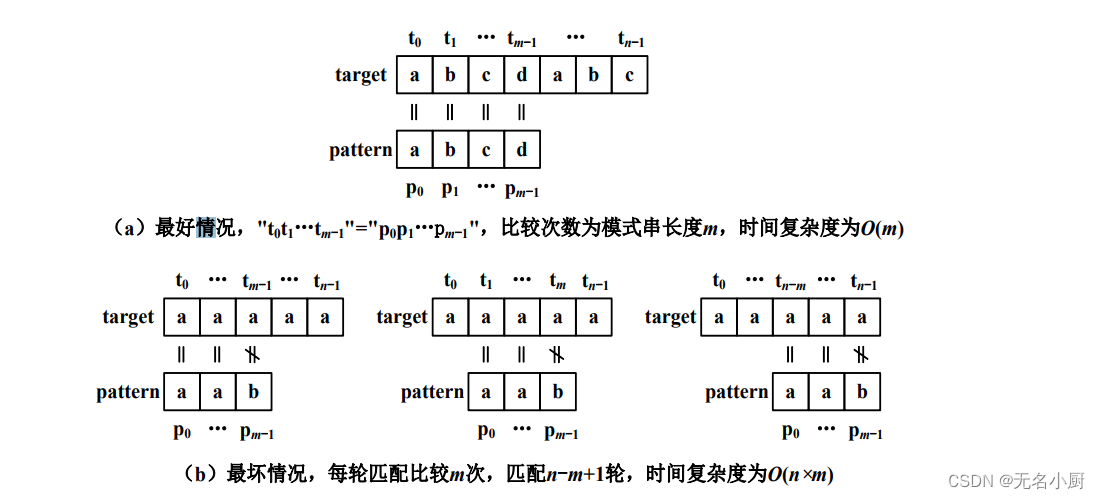
在这里插入图片描述

6.KMP算法描述与实现

 public static int indexOf(String target, String pattern, int begin)
    {
        int n=target.length(), m=pattern.length();
        if (begin<0) //对begin容错，若begin<0，从0开始
            begin = 0;
        if (n==0 || n<m || begin>=n) //若目标串空、较短或begin越界，不需比较
            return -1;
        next = getNext(pattern); //返回模式串pattern的next数组
        int i=begin, j=0; //i、j分别为目标串、模式串比较字符下标
        while (i<n && j<m)
        {
            if (j==-1 || target.charAt(i)==pattern.charAt(j))
            //若当前两字符相等，则继续比较后续字符
            {
                i++;
                j++;
            }
            else //否则，下次匹配，目标串下标i不回溯
            {
                j=next[j]; //模式串下标j退回到下次比较字符序号
                if (n-i+1<m-j+1) //若目标串剩余子串的长度不够，不再比较
                    break;
            }
        }
        if (j==m) //匹配成功
            return i-j; //返回匹配的子串序号
        return -1; //匹配失败
    }

6.1 计算next数组

KMP算法充分利用前一次匹配的比较结果，由next[j]逐个递推计算得到
next[j+1]。说明如下：
（1）约定next[0]=-1，-1表示下次匹配从ti+1与p0开始比较；有next[1]=0。
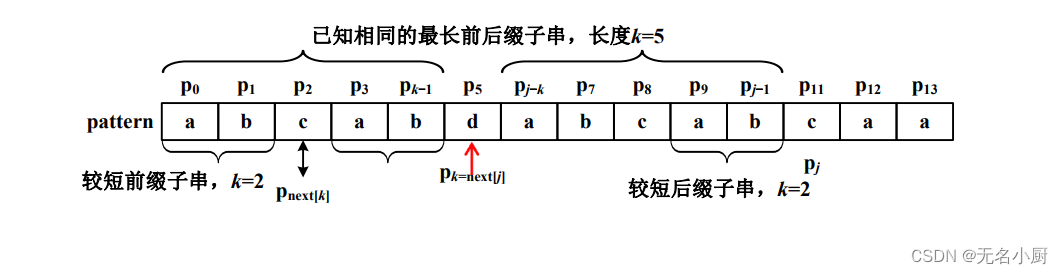
（2）如果pk=pj，即”p0…pk-1pk”=“pk-j…pj-1pj”，存在相同的前后缀子串，长度为k+1，则下一个字符pj+1的next[j+1]=k+1=next[j]+1。
例如：”abcabc”，已求得next[4]=1（j=4，k=1），此时p3=p0=‘a’，而p4=p1=‘b’，则”p3p4”=“p0p1”，所以next[5]=next[4]+1=2。
（3）如果pk≠pj，在”p0…pj”中寻找较短的前后缀子串，较短前后缀子串的长度为next[k]，则k=next[k]；再比较pj与pk，继续执行，寻找相同的前后缀子串。

在这里插入图片描述

 private static int[] getNext(String pattern) 
 //返回模式串pattern的next数组
    {
        int j=0, k=-1, next[]=new int[pattern.length()];
        next[0]=-1;
        while (j<pattern.length()-1)
            if (k==-1 || pattern.charAt(j)==pattern.charAt(k))
            {
                j++;
                k++;
                next[j]=k;
            }
            else k=next[k];
        return next;
    }