在x264源码里，void x264_frame_deblock_row( x264_t *h, int mb_y )函数中定义了如下的宏片段，这段代码旨在完成对MB的deblocking 操作，其中针对edge 取不同的值的时候，有的做deblocking， 有的不做，看这部分代码的时候我也是存在疑惑，后面结合H.264 spec draft， 一切就清楚明了了。
防止自己忘记，记录一下。

#define FILTER( intra, dir, edge, qp, chroma_qp )\
        do\
        {\
            if( !(edge & 1) || !transform_8x8 )\
            {\
                deblock_edge##intra( h, pixy + 4*edge*(dir?stride2y:1),\
                                     stride2y, bs[dir][edge], qp, a, b, 0,\
                                     h->loopf.deblock_luma##intra[dir] );\
                if( chroma_format == CHROMA_444 )\
                {\
                    deblock_edge##intra( h, pixuv          + 4*edge*(dir?stride2uv:1),\
                                         stride2uv, bs[dir][edge], chroma_qp, a, b, 0,\
                                         h->loopf.deblock_luma##intra[dir] );\
                    deblock_edge##intra( h, pixuv + uvdiff + 4*edge*(dir?stride2uv:1),\
                                         stride2uv, bs[dir][edge], chroma_qp, a, b, 0,\
                                         h->loopf.deblock_luma##intra[dir] );\
                }\
                else if( chroma_format == CHROMA_420 && !(edge & 1) )\
                {\
                    deblock_edge##intra( h, pixuv + edge*(dir?2*stride2uv:4),\
                                         stride2uv, bs[dir][edge], chroma_qp, a, b, 1,\
                                         h->loopf.deblock_chroma##intra[dir] );\
                }\
            }\
            if( chroma_format == CHROMA_422 && (dir || !(edge & 1)) )\
            {\
                deblock_edge##intra( h, pixuv + edge*(dir?4*stride2uv:4),\
                                     stride2uv, bs[dir][edge], chroma_qp, a, b, 1,\
                                     h->loopf.deblock_chroma##intra[dir] );\
            }\
        } while( 0 )

H.264 spec draft 中，针对哪些情况要做deblocking 有如下描述：


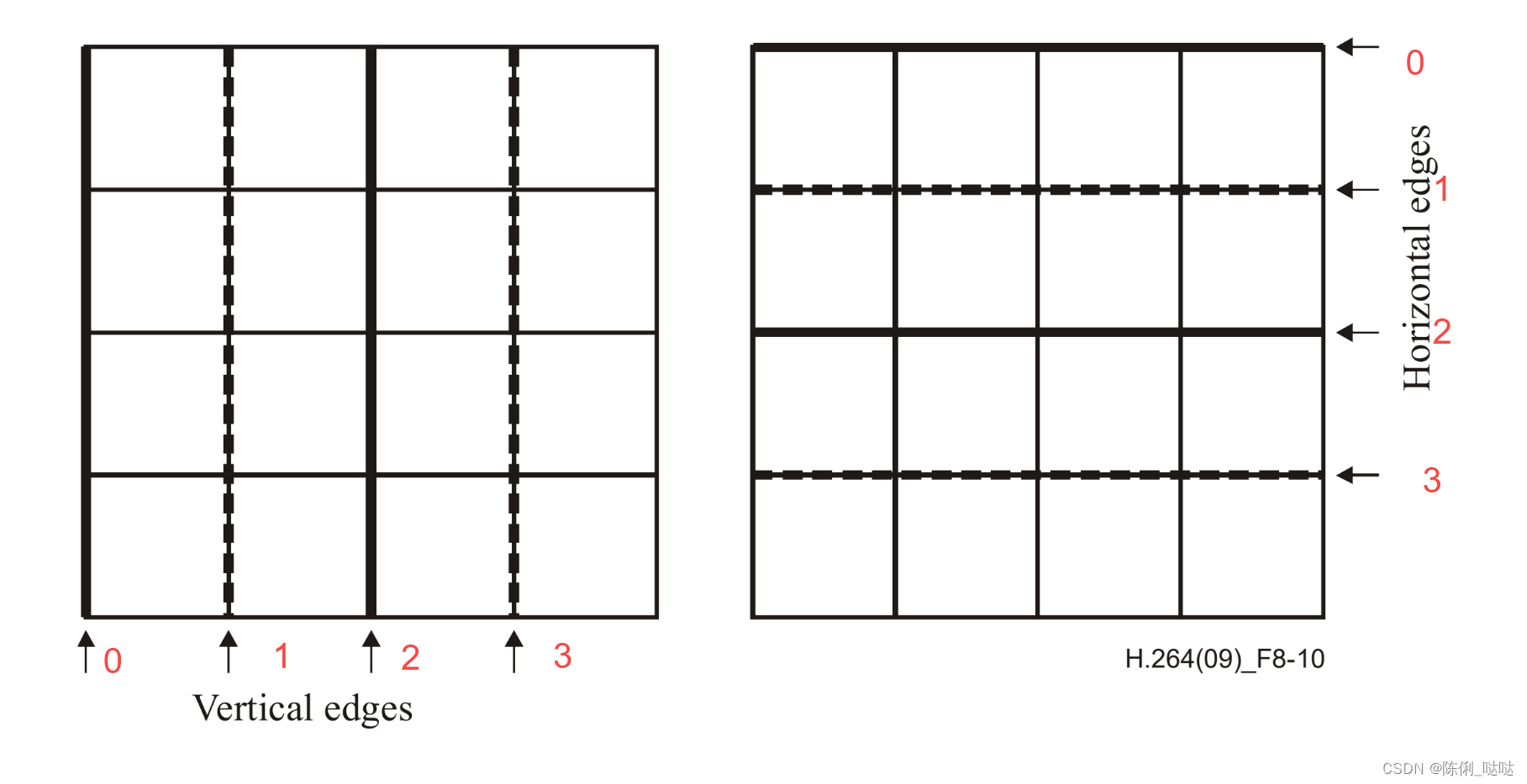
针对luma 做了如下约束：
若transform_8x8 没有打开，则luma 的 edge 0 1 2 3 均要做filter， 否则只有edge 0 2 做filter；

针对chroma 做了如下约束：
1.如果是4:2:0的YUV 格式，edge 0 2 做filter；
2.如果是4:2:2的YUV 格式，vertical 方向，edge 0 2 做filter， horizontal 方向， edge 0 1 2 3 均做filter；
3.如果是4:2:2的YUV 格式， transform_8x8=0时，均做滤波， 否则 edge 0 2 做滤波；
4.其他的YUV 格式（不存在chroma 分量），则不做chroma 滤波；

好记性不如烂笔头，希望这次能彻底记住不忘记~