论文不详细解读（一）—

论文不详细解读（一）——MoCo系列

news2025/11/1 6:52:07

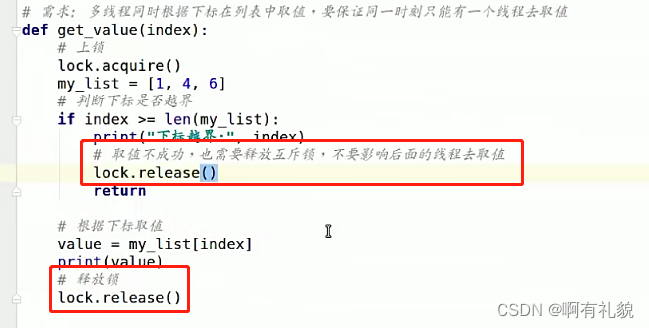
1. MoCo v1

论文名称： Momentum Contrast for Unsupervised Visual Representation Learning

开源地址：https://github.com/facebookresearch/moco
大佬详细解读：https://zhuanlan.zhihu.com/p/382763210

motivation

原始的端到端自监督方法：
给定样本 $x_q$ ，数据增强得到正样本 $x_k$ ，batch内的其余样本作为负样本

原始样本 $x_q$ 输入到Encoder $f_q$ 中，正样本和负样本均输入到Encoder $f_k$ 中，通过Contrastive loss来更新2个Encoder $f_q$ 和 $f_k$ 的参数

Contrastive loss一般为InfoNCE:
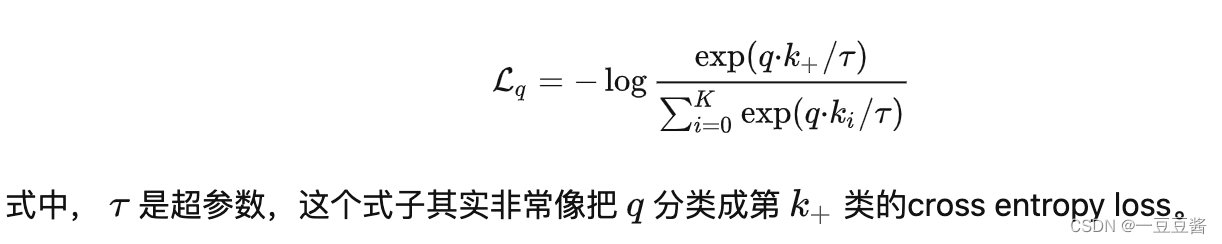
在这里插入图片描述

毫无疑问，batch size 越大效果越好，但是受显存影响（2个encoder的全量数据都用于更新两个encoder的参数），batchsize不能设置过大，如何获得更多的负样本？

MoCo v1之前的做法：
正样本的生成方式不变（数据增强），采用一个较大的memory bank 用来存储负样本，每次训练从中采样一批负样本出来 $k_{sample}$ ，loss只更新Encoder $f_q$ 的参数，和几个采样的 $k_{sample}$ 值。因为这时候没有了 Encoder $f_k$ 的反向传播，所以支持memory bank容量很大。

上述方法存在的弊端：
Encoder $f_q$ 每个step都会更新，但是某一个 $k_{sample}^i$ 可能很多个step才被采样到更新一次，而且一个epoch只会更新一次。这样最新的 query 采样得到的 key 可能是好多个step之前的编码器编码得到的 key，因此丧失了一致性。

MoCo的解决方法

momentum (移动平均更新模型权重) 与queue (字典)

假设 Batch size 的大小是 $N$ ，现在有个队列 Queue，这个队列的大小是 $K (K > N)$ ，为了方便更新， $K$ 一般是 $N$ 的整数倍（代码里面 $K = 65536$ ）。

如上图所示，有俩网络，一个是 Encoder ，另一个是Momentum Encoder 。这两个模型的网络结构是一样的，初始参数也是一样的 (但是训练开始后两者参数将不再一样了)。 $f_q$ 与 $f_{mk}$ 是将输入信息映射到特征空间的网络。

样本 $x$ 经过两种数据增强分别得到样本 $x_q$ 和 $x_k$ ， $x_q$ 经过Encoder $f_q$ 得到特征 $q$ （维度 $N \times C$ ）， $x_k$ 经过Encoder $f_{mk}$ 得到特征 $k$ （维度 $N \times C$ ）， $q$ 和 $k$ 为两个正样本特征
其中k=k.detach()，不使用梯度更新 $f_{mk}$ 的参数

moco伪代码

f_k.params = f_q.params # 初始化
for x in loader: # 输入一个图像序列x，包含N张图，没有标签
    x_q = aug(x) # 用于查询的图（数据增强得到）
    x_k = aug(x) # 模板图（数据增强得到），自监督就体现在这里，只有图x和x的数据增强才被归为一类
    q = f_q.forward(x_q) # 提取查询特征，输出NxC
    k = f_k.forward(x_k) # 提取模板特征，输出NxC
    # 不使用梯度更新f_k的参数，这是因为文章假设用于提取模板的表示应该是稳定的，不应立即更新
    k = k.detach() 
    # 这里bmm是分批矩阵乘法
    l_pos = bmm(q.view(N,1,C), k.view(N,C,1)) # 输出Nx1，也就是自己与自己的增强图的特征的匹配度
    l_neg = mm(q.view(N,C), queue.view(C,K)) # 输出Nxk，自己与上一批次所有图的匹配度（全不匹配）
    logits = cat([l_pos, l_neg], dim=1) # 输出Nx(1+k)
    labels = zeros(N)   # 正样本全在第0位
    # NCE损失函数，就是为了保证自己与自己衍生的匹配度输出越大越好，否则越小越好
    loss = CrossEntropyLoss(logits/t, labels) 
    loss.backward()
    update(f_q.params) # f_q使用梯度立即更新
    # 由于假设模板特征的表示方法是稳定的，因此它更新得更慢，这里使用动量法更新，相当于做了个滤波。
    f_k.params = m*f_k.params+(1-m)*f_q.params 
    enqueue(queue, k) # 为了生成反例，所以引入了队列
    dequeue(queue)

下图展示的是logits某一行的信息，这里的 K=2。
在这里插入图片描述

训练参数：

优化器：SGD，weight decay: 0.0001，momentum: 0.9。
Batch size： 256
初始学习率： 0.03，200 epochs，在第120和第160 epochs时分别乘以0.1，结束时是0.0003。

附上一些思考：

🌱 Momentum Encoder输入的是正样本 $x_k$ 和负样本queue中的全量样本（区别于memory bank 采样输入负样本）
🌱 负样本队列queue的更新条件是什么？
队列存满会把最旧的样本batch替换成最新的batch，队列长度K不是样本总数量，而是远远小于总数量的（65535 vs 几百万），所以queue内存在和query正样本的概率比较小
🌱 数据增强的方式：

Randomly resized image + random color jittering
Random horizontal flip
Random grayscale conversion

此外，作者还把 BN 替换成了 Shuffling BN，因为 BN 会欺骗 pretext task，轻易找到一种使得 loss 下降很快的方法。
在这里插入图片描述

🌱 对比端到端自监督的方法，MoCo的负样本数量为 $K$ （queue长度），端到端负样本数量为 $ba t c h s i ze - 1$
🌱 为什么momentum encoder参数更新m=0时会训练失败而端到端自监督训练时却没有失败？
对于动量参数更新m的消融实验：
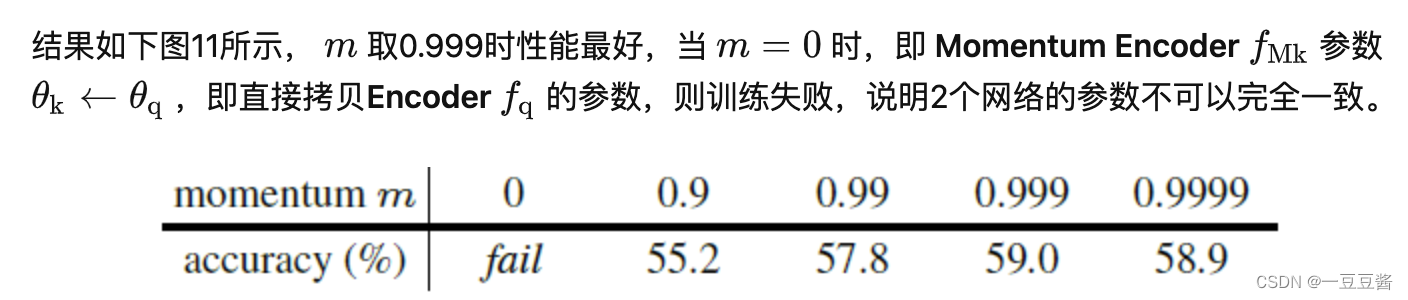
在这里插入图片描述
m=0说明两个encoder的参数完全一致，而端到端的训练，是两个网络均使用梯度更新，网络参数不一定一致，所以训练不会失败