原视频为左程云的B站教学

---

以下所有的swap()函数，函数定义为

void swap(int& a, int& b)
{
	int t = a;
	a = b;
	b = t;
}
// 也可以用异或，但不能传入同一个变量，可以是不同变量相同值
void swap(int& a, int& b)
{
	a = a ^ b;
	b = a ^ b;
	a = a ^ b;
}

1 冒泡排序$O(N^2)$（与数据状况无关）

最基础、最简单的排序，没啥好说的

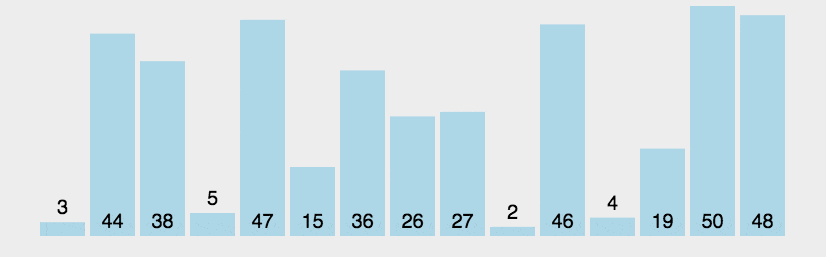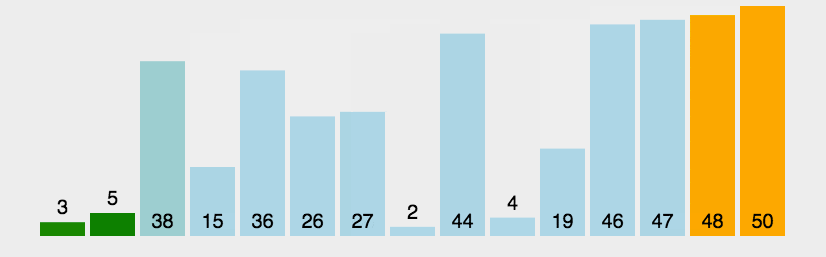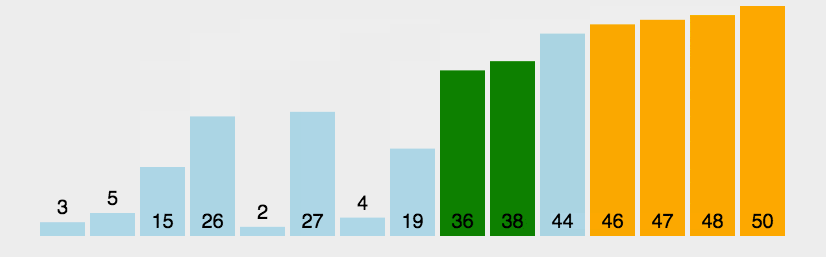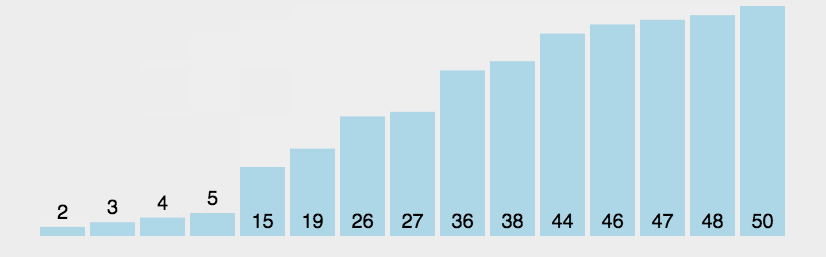
#incldue <vector>
void bubbleSort(std::vector<int>& arr) 
{
    for (int i = 0; i < arr.size() - 1; i++) {
        for (int j = 0; j < arr.size() - 1 - i; j++) {
            if (arr[j] > arr[j+1]) {        // 相邻元素两两对比
				swap(arr[j], arr[j+1]);
            }
        }
    }
}

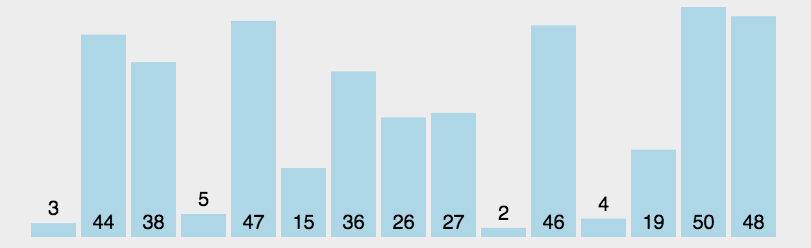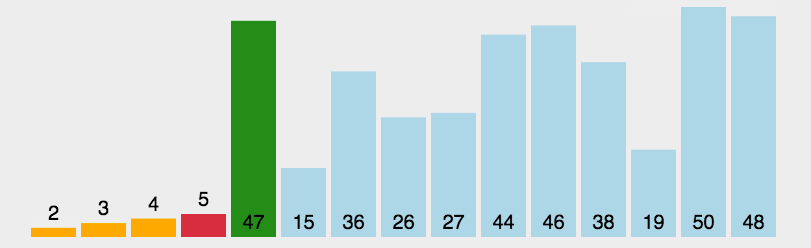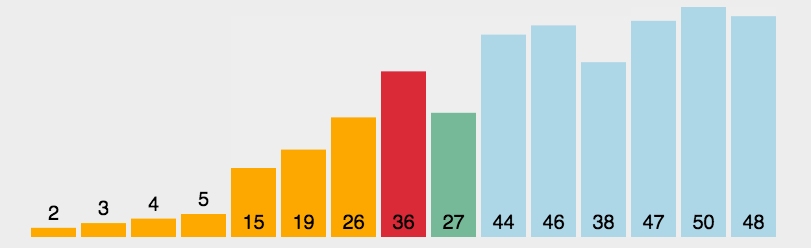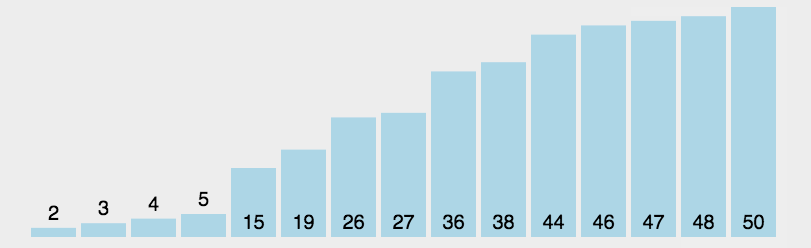
2 选择排序$O(N^2)$（与数据状况无关）

基本思想是每次从待排序的元素中选择最小（或最大）的元素，放到已排序序列的末尾。选择排序的主要步骤如下：

• 1.遍历待排序序列，设定当前位置为最小值的位置。
• 2.从当前位置开始，依次比较当前元素与后面的元素，找到最小的元素，记录其位置。
• 3.将最小元素与当前位置的元素进行交换。
• 4.重复步骤2和步骤3，直到遍历完整个序列。
  

#include<vector>
void selectionSort(std::vector<int>& arr)
{
	int len = arr.size();
	if (arr.empty() || len < 2) return;

	for (int i = 0; i < len -1; i++){ // len -1 位置不用再循环了，因为最后剩一个必然是最值
		int minIndex = i;		// 在i ~ len-1 上寻找最小值的下标
		for (int j = i; j < len - 1; j++){
			minIndex = arr[j] < arr[minIndex] ? j : minIndex;
		}
		swap(arr[minIndex], arr[i]);
	}
}

3 插入排序$O(N^2)$（与数据状况相关）

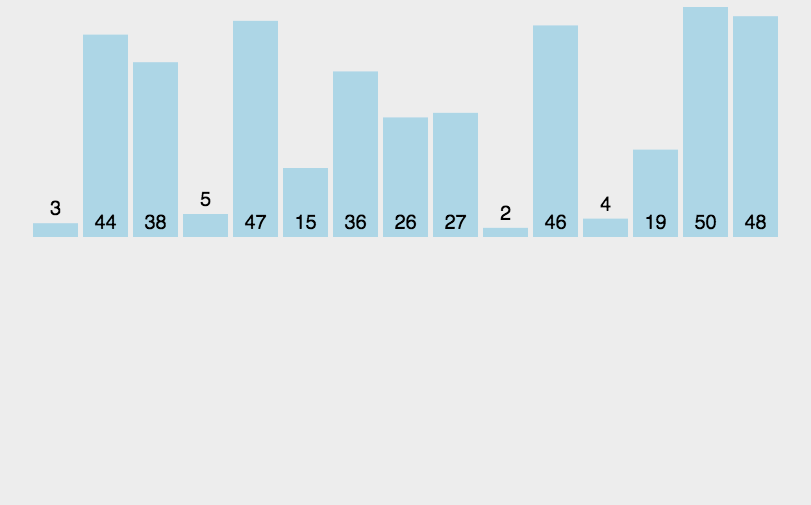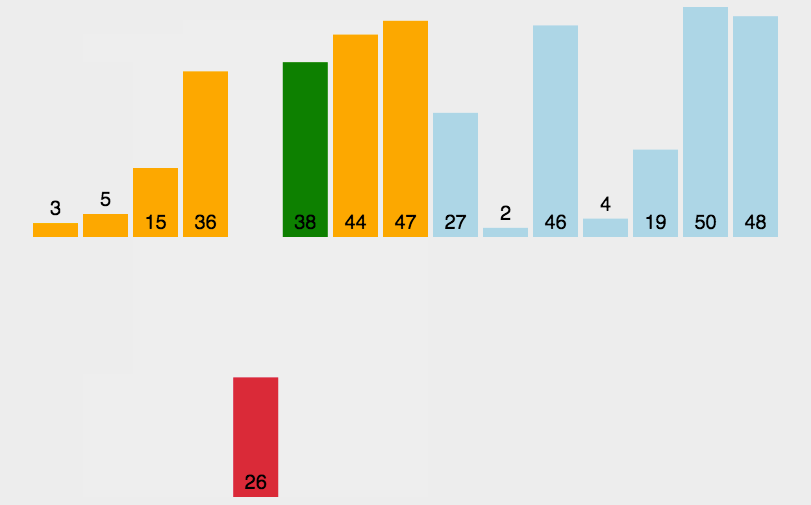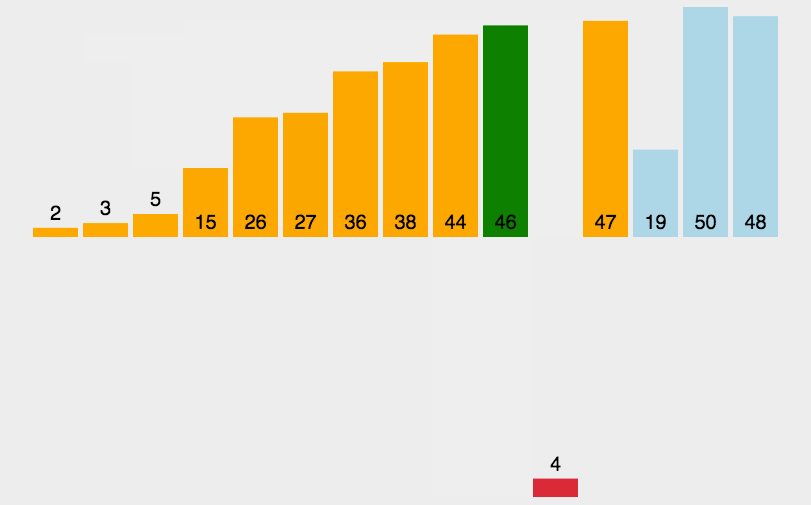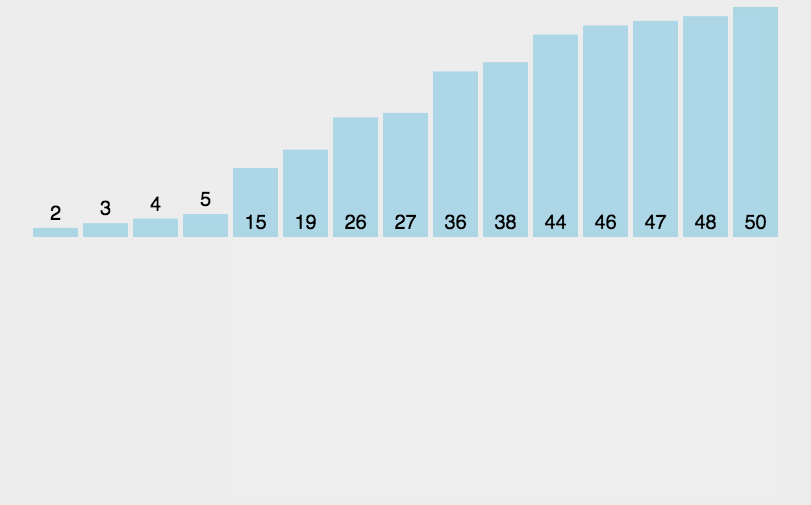
原理类似于对扑克牌手牌进行排序的过程。将未排序的元素逐个插入到已排序部分的合适位置。

逻辑顺序为先做到0~0有序， 然后0~1有序， 0~2 … 0~n-1有序

算法流程为：

• 1.从第一个元素开始，该元素可以认为已经被排序。
• 2.从未排序部分取第一个值，插入到已排序部分的适当位置。这个位置的选取方式为：把当前未排序值与左邻值对比，如果更小则交换位置。直到遇到边界或不比左邻值小则结束。（内循环：找适当位置插入）
• 3.重复步骤2，直到所有元素都被插入到已排序序列中。（外循环：遍历每个未排序的数）

这个不像冒泡排序和选择排序是固定操作(数据状况无关)。插入排序中，如果给的就是有序的，那就外层循环每次比一下就完成了所以会是O(N), 但我们说时间复杂度都是 worst case 所以还是 $O(N^2)$

#include <vector>
void insertionSort(std::vector<int>& arr)
{
	int len = arr.size();
	if (arr.empty() || len < 2) return;
	// 0~0已经有序了
	for (int i = 1; i < len; i++){ 	// 0~i做到有序
		// 把当前值(j+1)对比左邻值(j)，比他小则交换，不满足循环条件则说明找到合适位置了
		for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--){ 
			swap(arr[j+1], arr[j]);
		}
	}
}

在内层循环中，我们将当前元素 arr[j + 1] 与其左邻元素 arr[j] 进行比较，更小则换位，直到找到合适的插入位置。
循环结束（找到合适的位置）条件为：达到左边界 or 当前值比左邻值大

继续往下看建议先掌握 二分查找

4 归并排序($O(NlogN)$)（数据状况无关）

它的核心思想是将待排序的序列不断划分成更小的子序列，直到每个子序列只有一个元素，然后再将这些子序列两两合并，直到最终整个序列有序。

下面是归并排序的一般步骤：

• 分割：将待排序的序列从中间位置分割成两个子序列，不断递归地将每个子序列继续分割，直到每个子序列只剩下一个元素。
• 合并：将两个有序的子序列合并成一个有序序列。从两个子序列的第一个元素开始比较，将较小的元素放入临时数组中，并将对应子序列的索引向后移动一位，直到其中一个子序列的元素全部放入临时数组中。然后将另一个子序列的剩余元素直接放入临时数组中。
• 重复合并：重复进行合并操作，直到所有子序列都合并为一个有序序列。

始终都是 O(nlogn) 的时间复杂度，与数据无关。虽然相对前面的冒泡、选择、插入排序更快，但是需要额外的内存空间。

下图对于这个过程的描述是非常准确的，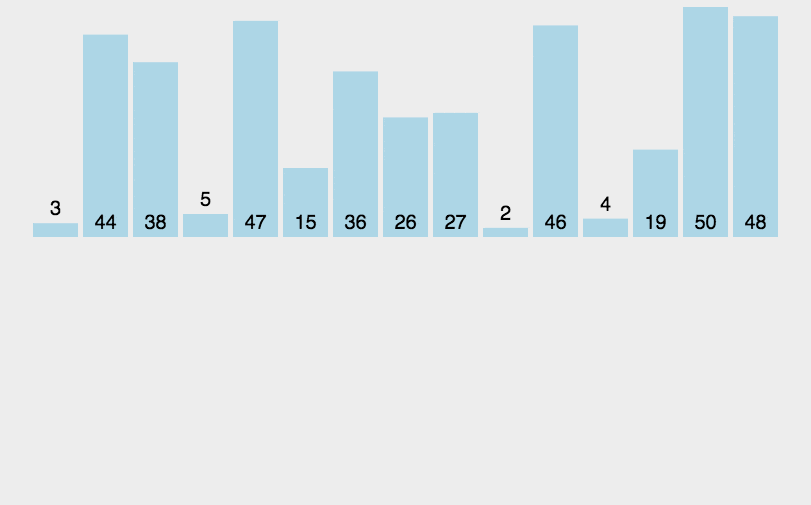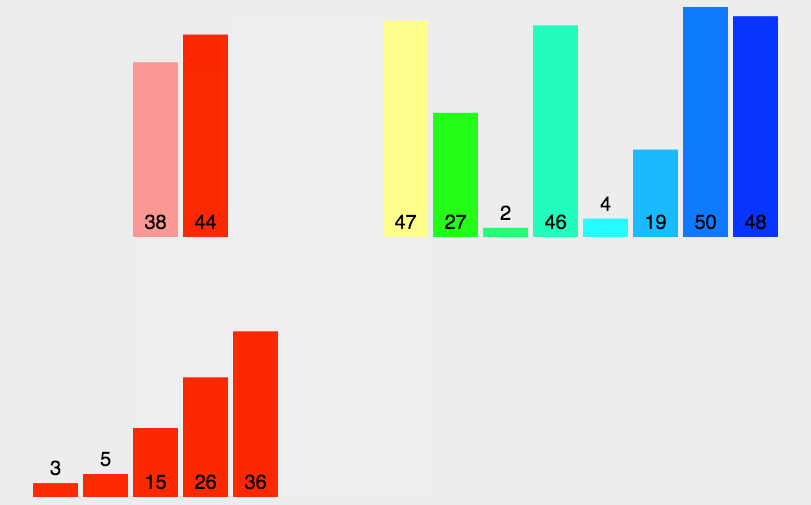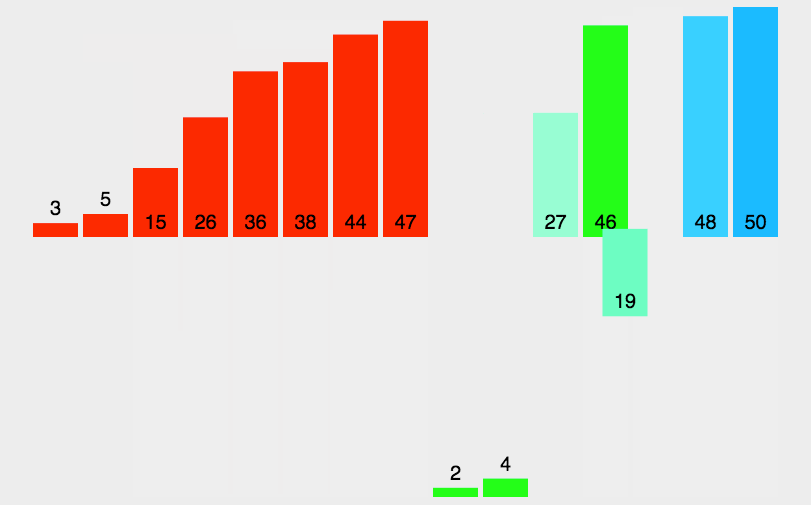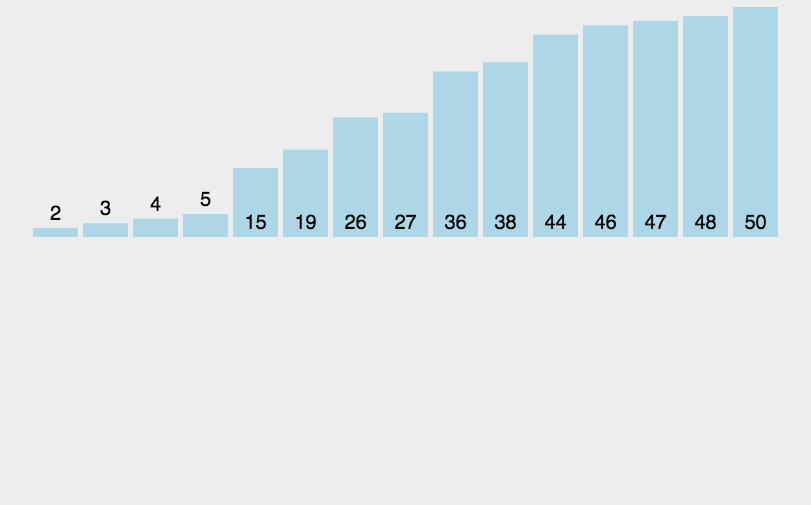

// 第二阶段：merge阶段时，L~M 和 M~R 之间的数必然有序
void merge(std::vector<int>& arr, int L, int M, int R)
{
	std::vector help(R - L + 1);
	int i = 0;
	int p1 = L;
	int p2 = M + 1;
	while (p1 <= M && p2 <= R){ //类似链表合并，把两个子数组中的元素从小到大放到help数组
		help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
	}
	while (p1 <= M){ // 如果左边部分还有剩的，全部加到help中
		help[i++] = arr[p1++];
	}
	while (p2 <= R){ // 同理如果右边还有剩的
		help[i++] = arr[p2++];
	}

	// 结束，把临时数组的内容覆盖到原数组中
	for (i = 0; i < R - L + 1; i++){
		arr[L + i] = help[i]; // 注意arr从L位置开始写入的
	}
}

// 务必先看这个函数 这算是第一阶段拆分
void mergeSort(std::vector<int>& arr, int L, int R)
{
	if (L == R) return;	// 拆分完毕，不能再拆了
	
	int mid = L + ((R - L) >> 1);
	mergeSort(arr, L, mid);
	mergeSort(arr, mid+1, R);
	merge(arr, L, mid, R); // 执行到这一步的条件是 L == mid 且 mid+1 == R
}