各家大厂面试时都喜欢出一些逻辑题，简单的考验一下应试者的逻辑思维能力。

题目是：现在有64匹赛马和8条赛道，最少需要多少轮比赛才能选出最快的4匹马。

        依据现实情况来说，这个问题很好回答。需要经过小组赛，16强赛，半决赛，决赛。四轮比赛就能决出最快的4匹马。这里一共需要四轮比赛。

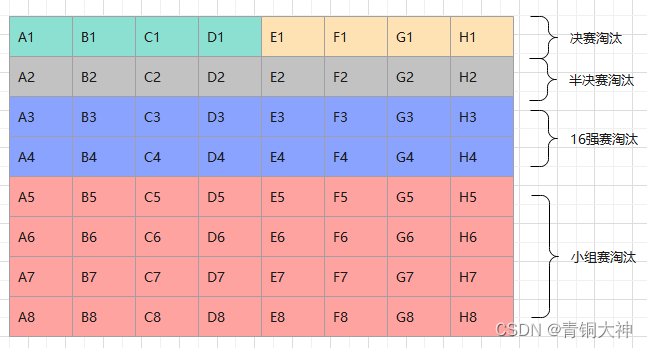
        但是呢，如果是考逻辑题就有优化的空间的，我们先列出我们这64匹马，将他们分为A,B,C,D,E,F,G,H这8组。 

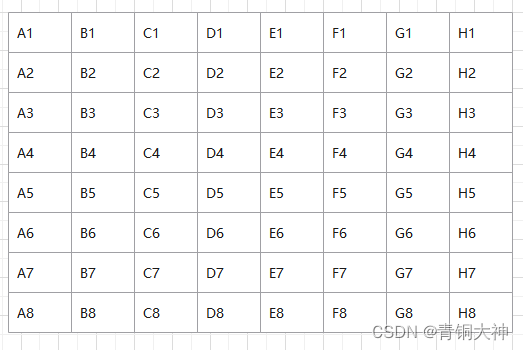
         我们先进行第一轮比赛，这8组进行组内比赛，决出每组的前4名，晋级下一轮比赛。

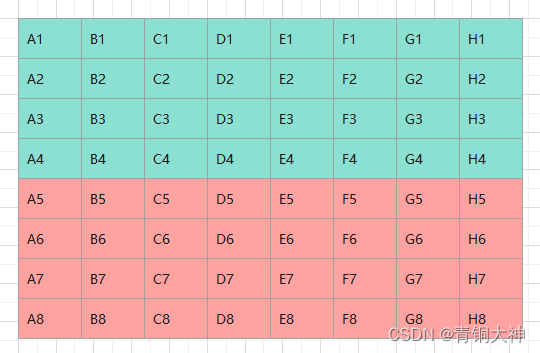
 每组后四名被淘汰。

        第二轮比赛，取第一轮比赛中决出的每组第一名站出来比试一场，他们代表了小组的荣誉。

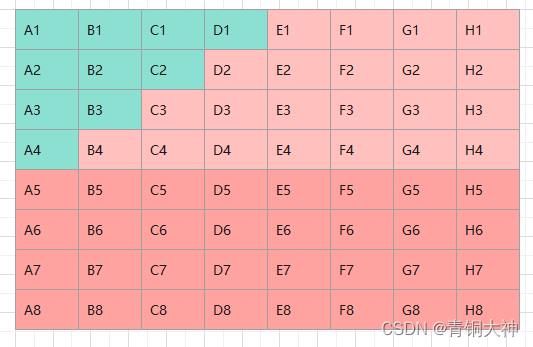
第一名所在组全员晋级下一轮比赛，第二名所在组淘汰一名，第三名所在组淘汰两名，第四名所在组讨论三名，后续组全员淘汰。

       

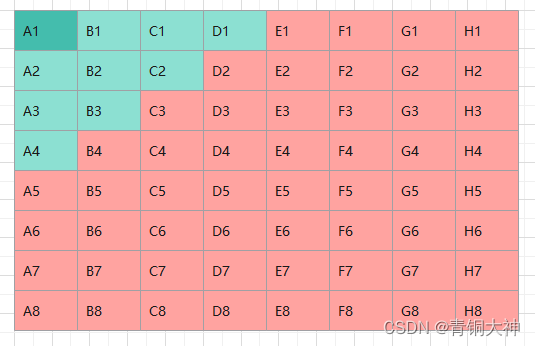
        接下来一轮怎么比赛就需要仔细斟酌一下了，由于A1是无可争议的第一，稳进前4，所以第三轮比赛不需要考虑A1，只考虑剩下的9匹马争夺剩下的三个名额。这里就需要对暂时放弃哪匹马做一个取舍。

        首先A2，A3，A4，B2，B3，C2这六匹马由于没有参加第二轮比赛，所以必须要参加第三轮比赛。那我们就需要在剩下的三匹马当中舍弃一个。那么我们该舍弃哪一个呢？我们舍弃了D1，因为D1在第二轮中排名第四，被淘汰的几率还是很大的，而且只有当C1在第三轮比赛中，排名第三的情况下，才需要出场比赛，情况唯一不复杂。

        这里第三轮比赛没有上场的D1怎么办呢？这里分为两种情况，如果C1也被淘汰了，那么D1也一定会被淘汰。如果C1是第三，我们还需要D1和第四名比试一场，来确定第四是哪匹马。

        这样我们只需要三轮比赛就找到了64匹马中最快的4匹马，比传统的公平竞技形式，少赛了一轮。