算法题 数组系列
- 一、找出数组中重复的数字
- 1.1、题目
- 1.2、解题思路1(排序法)
- 1.3、解题思路2(hash)
- 1.4、小结
- 二、二维数组中的查找
- 2.1、题目
- 2.2、理解题目
- 2.3、解题思路
- 2.3.1、暴力枚举
- 2.3.2、二分查找
- 2.3.3、对角线查询(Z型)
- 2.4、小结
- 总结
一、找出数组中重复的数字
1.1、题目
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
来源:力扣(LeetCode)。
1.2、解题思路1(排序法)
将数字排序,排序后的数字如果前一个元素和后一个元素相同(nums[i]==nums[i+1]),则就是一个重复数字。
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
int n=nums.size()-1;
sort(nums.begin(),nums.end());
while(n)
{
if(nums[n]==nums[n-1])
return nums[n];
n--;
}
return 0;
}
};
时间复杂度:O(n)。
空间复杂度:O(n)。不重复的每个元素都可能存入集合,因此占用 O(n)额外空间。
1.3、解题思路2(hash)
利用unordered_map来检查重复的数字。将数组的元素填入unordered_map<int,bool>,通过检查bool来判定重复的数字。
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
unordered_map<int, bool> map;
for(int num:nums)
{
if(map[num])
return num;
map[num]=true;
}
return -1;
}
};
执行用时:44 ms, 在所有 C++ 提交中击败了38.00%的用户
内存消耗:26.8 MB, 在所有 C++ 提交中击败了42.25%的用户
时间复杂度 O(N)。
空间复杂度 O(N)。
1.4、小结
排序法是比较容易想到的算法,核心是先排序再比较。hash方式也比较常用。
二、二维数组中的查找
2.1、题目
在一个 n * m 的二维数组中,每一行都按照从左到右 非递减 的顺序排序,每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
来源:力扣(LeetCode)
2.2、理解题目
二维数组中,从左到右是依次递增排序,从上到下是依次递增排序;给定一个数字,判断该数组中是否存在该数字。

2.3、解题思路
2.3.1、暴力枚举
暴力枚举:直接遍历整个矩阵matrix,判断target是否出现即可。
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int n=matrix.size();
if(n==0)
return false;
int m=matrix[0].size();
if(m==0)
return false;
if(target<matrix[0][0] || target>matrix[n-1][m-1])
return false;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(matrix[i][j]>target)
break;
else if(matrix[i][j]==target)
return true;
}
}
return false;
}
};
时间复杂度:O(nm)。
空间复杂度:O(1)。
2.3.2、二分查找
C++ STL标准库中还提供有 lower_bound()、upper_bound()、equal_range() 以及 binary_search() 这 4 个查找函数,它们的底层实现采用的都是二分查找的方式。
这里采用lower_bound()函数,在指定区域内查找不小于目标值的第一个元素。
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
for(const auto &m:matrix)
{
auto it= lower_bound(m.begin(),m.end(),target);
if(it!=m.end() && *it==target)
return true;
}
return false;
}
};
时间复杂度: O(n log m)。
空间复杂度:O(1)。
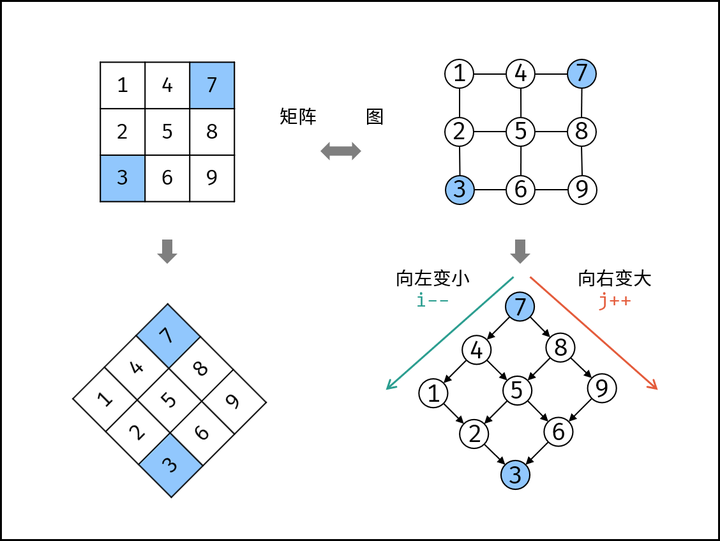
2.3.3、对角线查询(Z型)
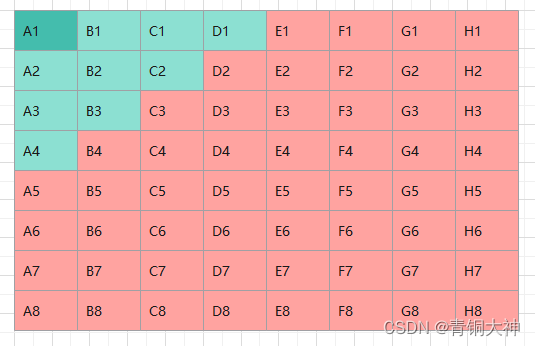
从二维数组的右上角[0,m]开始遍历,在每一步的遍历中,假设位置处于[x,y],就以matrix的左下角为左下角,[x,y]为右上角进行搜索,即行范围为x ~ m-1,列范围为0 ~ y。
如果matrix[x][y] == target,返回true。
如果matrix[x][y]>target,因为行是递增的,列也是递增的,那么y列的所有数都大于target,将y减一来缩小范围。
如果matrix[x][y]<target,因为行是递增的,列也是递增的,x加1来缩小范围。
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int n=matrix.size();
if(n==0)
return false;
int m=matrix[0].size();
if(m==0)
return false;
int x=0,y=m-1;
while(x<n && y>=0)
{
if(matrix[x][y]==target)
return true;
else if(matrix[x][y]>target)
y--;
else
x++;
}
return false;
}
};
时间复杂度:O(n+m)。
空间复杂度:O(1)。
优化:
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int n = matrix.size() - 1, m = 0;
while(n >= 0 && m < matrix[0].size())
{
if(matrix[n][m] > target) n--;
else if(matrix[n][m] < target) m++;
else return true;
}
return false;
}
};
2.4、小结
暴力枚举属于下下策,优先考虑使用对角线搜索(或称为z型搜索)。对角线搜索类似二叉树搜索数的遍历,将二维数组旋转45°,对于每个元素,其左分支元素更小、右分支元素更大。因此,通过从 “根节点” 开始搜索,遇到比 target 大的元素就向左,反之向右,即可找到目标值 target。
总结
一定要做好总结,特别是当没有解出题来,没有思路的时候,一定要通过结束阶段的总结来反思犯了什么错误。解出来了也一定要总结题目的特点,题目中哪些要素是解出该题的关键。不做总结的话,花掉的时间所得到的收获通常只有 50% 左右。
在题目完成后,要特别注意总结此题最后是归纳到哪种类型中,它在这种类型中的独特之处是什么。