函数	备注
triangular(left, mode, right)	三角形分布
uniform([low, high])	均匀分布

均匀分布

所谓均匀分布，就是在事件空间中，所有事件的概率都是相等的连续分布，其概率密度为

$$f(x)=\frac{1}{b-a},x\in (a,b)$$

易得其均值为$\frac{a+b}{2}$，方差为$\frac{(b-a{)}^2}{12}$。

在numpy.random中，uniform用于生成均匀分布的随机数，其输入参数分别为随机数下限和上限，示例如下面代码所示

import matplotlib.pyplot as plt
import numpy as np
from numpy.random import uniform

xs = uniform(1, 5, size=20000)
plt.hist(xs, 100)
plt.show()

其分布为

毫无疑问，均匀分布是最简单的分布函数，在$(a,b)$区间内，所有点差不多构成了一个矩形，所以均匀分布也叫矩形分布。

和矩形分布相似，概率密度函数为三角形的分布，就是三角形分布。

三角形分布

对于下限为$a$，上限为$b$，众数为$c$的三角分布，其概率密度函数为

$$f(x)=\{\begin{array}{r}\frac{2(x-a)}{(b-a)(c-a)}a⩽x⩽c\\ \frac{2(b-x)}{(b-a)(b-c)}c<x⩽b\end{array}$$

在numpy.random中，trangular用于生成三角形分布的随机数，其输入参数分别为随机数下限、众数和上限，示例如下面代码所示

from numpy.random import triangular

xs = triangular(1, 3, 5, size=20000)
plt.hist(xs, 100)
plt.show()

效果如图所示

均匀分布和三角形分布之间的关系

若两个随机变量$X_1,X_2$符合均匀分布，则$X_1+X_2$符合三角形分布。

x1 = uniform(1,5,size=20000)
x2 = uniform(3,6,size=20000)
plt.hist(x1+x2, bins=100)
plt.show()

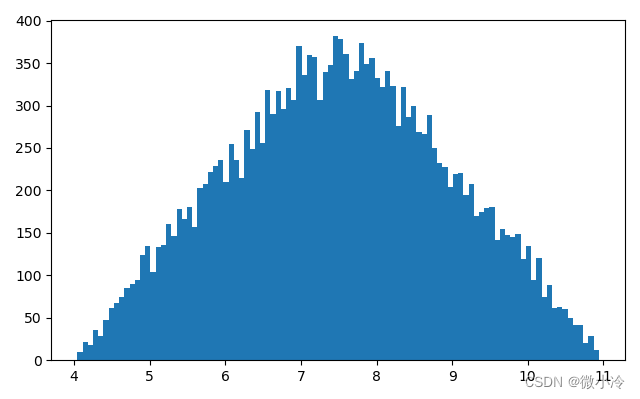
其分布的形状果然变成了三角形。

记X1的下限与上限为$a_1,b_1$，X2的下限与上限分别为$a_2,b_2$，从这个三角形分布的特点可以看出，三角形分布的下限和上限分别是$a_1+a_2,b_1+b_2$，其众数为$\frac{a_1+b_1+a_2+b_2}{2}$。

而且两组均匀分布的随机变量相减，其结果也是三角形分布

x1 = uniform(1,5,size=20000)
x2 = uniform(3,6,size=20000)
plt.hist(x1-x2, bins=100)
plt.show()

二者的区别无非是差个正负号而已。