springboot中自定义JavaBean返回的json对象属性名称大写变小写问题

开发过程中发现查询返回的数据出现自定义的JavaBean的属性值大小写格式出现问题，导致前端无法接受到数据，目前有四种解决方法，根据大佬的经验之谈，前两种是最简单便捷的，后两种是比较通用的方法。

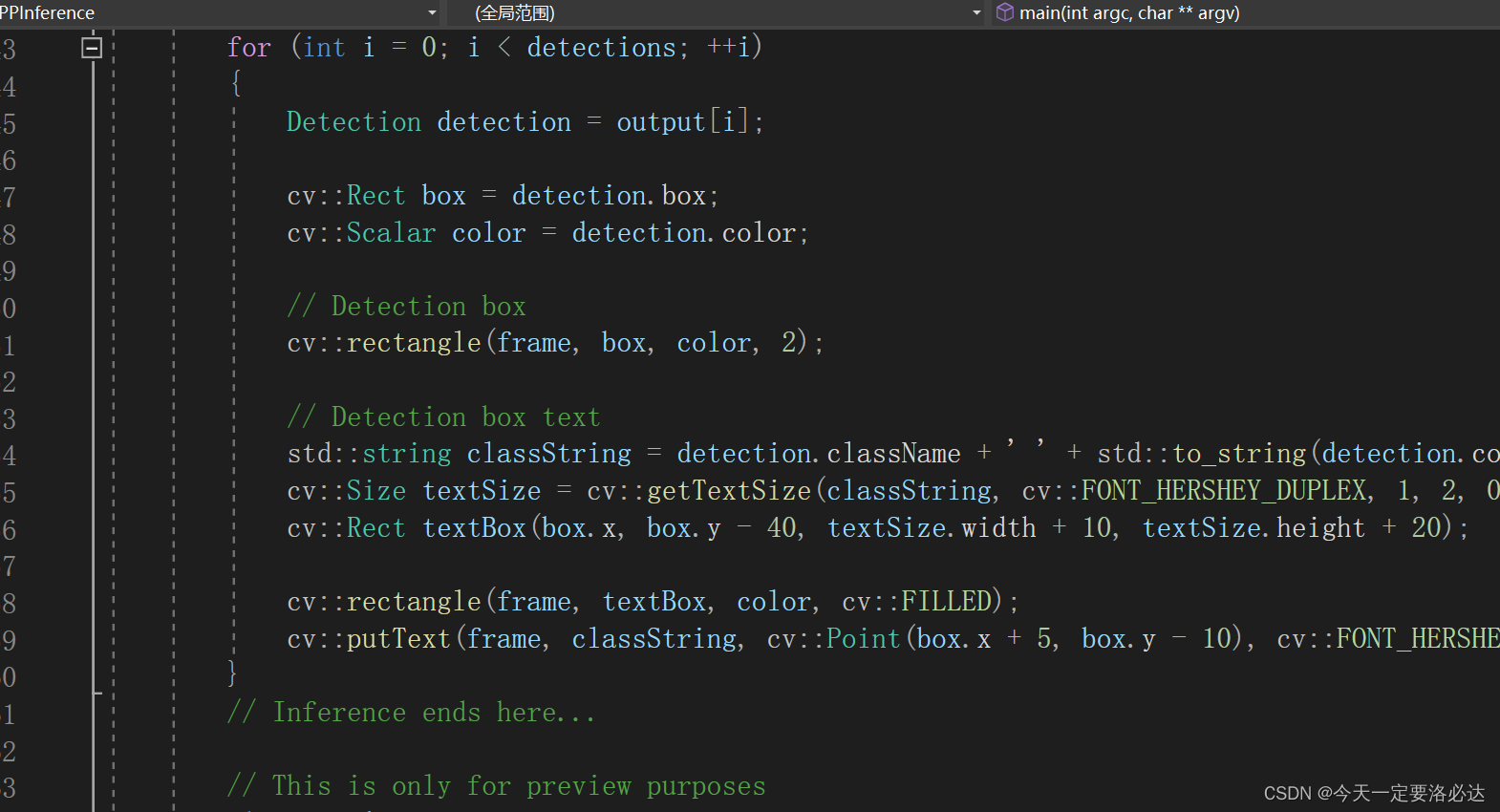
具体原因如下图：

一、继承类

一般在vo层（可自行理解，阿里巴巴的编程规范）自定义JavaBean来封装数据返回给前端，都是需要用到多表查询，或者有额外的属性增加时需要创建。

例如：人的javaBean最好的方式是继承一个学生的javaBean在添加新的属性，这样再人的JavaBean中没有问题，学生的JavaBean返回的数据也是正常的，不会出现因为@Data注解导致的bug。

二、手动添加Get方法

这有可能是由于Lombok中的@Data注解导致的bug，手动添加get和set方法也可以解决该问题。（尝试了返回的格式是正常的）

三、@JsonProperty

其它博主的解决方案：字段属性加上注解@JsonProperty("aAnimalId")指定序列化后的名称，字段属性的get方法加上注解@JsonIgnore。

本人尝试的结果：在字段属性加上注解@JsonProperty("aAnimalId")，接口返回数据的key就恢复正常了，或许是我和@Data混用的原因。但是分析了一下发现结果如下：

结果分析：

把首字母变成大小，从而和springboot返回json对象把字母变成小写相互抵消，从而导致可以返回正常的格式（自我理解，不确定对不对），但问题de到解决。各位可以尝试尝试，能解决开发问题的就是好办法。

四、spring-boot json(jackson)属性命名策略

全局配置命名策略，未尝试，大佬叫我了解了解，会有一定的收获。

spring:
　　jackson:
　　　　property-naming-strategy: SNAKE_CASE

记录每一个学习瞬间