前言

损失函数的作用是衡量模型预测值与真实值之间的差异，从而评估模型的性能，并通过优化算法（如梯度下降）来调整模型参数，使得损失函数的值最小化，进而提高模型的预测准确性。
具体来说，损失函数通常用于监督学习中，给定样本的特征和标签，模型根据特征预测标签，并将预测值与真实值进行比较，计算出损失值。优化过程就是在不断地调整模型参数，使得损失值越来越小。因此，损失函数是优化算法的重要组成部分，它决定了模型优化的方向和速度。
不同的损失函数适用于不同的任务和场景，例如均方误差适用于回归问题，交叉熵损失适用于分类问题，对比损失适用于相似度度量问题等等。因此，选择合适的损失函数对于模型训练和性能提升都至关重要。

均方误差（MSE）

$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$ 其中，$y_i$为真实值，$\widehat{y_i}$为预测值，$n$为样本数。

适用于回归问题，目标是最小化预测值与真实值之间的平方差，与其他损失函数无直接关联。

交叉熵损失（Cross-Entropy Loss）

$$CE=-\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^m{y}_{ij}\log \widehat{y_{ij}}$$ 其中，$y_{ij}$为第$i$个样本的第$j$个类别的真实标签，$\widehat{y_{ij}}$为第$i$个样本的第$j$个类别的预测值，$n$为样本数，$m$为类别数。

与最大似然估计相等价：最大化似然函数等价于最小化交叉熵损失函数，因此交叉熵损失函数也可以用于模型参数的最大似然估计。

适用于分类问题，目标是最小化预测值与真实值之间的交叉熵，常与Softmax函数结合使用，计算每个类别的概率分布。与对比损失、余弦相似度损失和Triplet损失不同，交叉熵损失不涉及样本之间的相似度度量。

假设我们要对一张手写数字图片进行分类，图片的标签为数字1，我们希望训练一个模型来正确地识别这张图片。首先，我们将这张图片输入到模型中，模型会输出一个长度为10的向量，表示这张图片属于10个数字中的每一个数字的概率。
假设模型输出的向量为[0.2, 0.6, 0.05, 0.02, 0.01, 0.01, 0.01, 0.05, 0.01, 0.04]，其中第二个元素0.6最大，因此模型预测这张图片属于数字2的概率最高。但是，我们知道这张图片的真实标签是数字1，因此我们需要计算模型预测值与真实值之间的差距，用交叉熵损失函数来衡量这个差距。
交叉熵损失函数的计算公式为：$L_{CE}=-{\sum }_{i=1}^n{y}_i\log (p_i)$，其中$n$表示类别数，$y_i$表示第$i$个类别的真实标签（0或1），$p_i$表示模型预测这个样本属于第$i$个类别的概率。在这个例子中，真实标签为数字1，因此$y_1=1$，其余的$y_i$都为0，模型预测数字1的概率为$p_1=0.2$，因此交叉熵损失为$L_{CE}=-(1\times \log (0.2)+0\times \log (0.6)+0\times \log (0.05)+...+0\times \log (0.04))=-\log (0.2)\approx 1.61$。
我们希望模型的预测值与真实值之间的差距越小越好，因此我们需要通过优化算法（如梯度下降）来调整模型参数，使得交叉熵损失最小化。在训练过程中，我们会将每个样本的交叉熵损失累加起来，得到整个训练集上的平均损失，作为模型的性能指标。通过不断迭代，我们可以让模型逐渐学习到更好的特征表示，提高分类准确率。

对比损失（Contrastive Loss）

$$L=\frac{1}{2n}\sum _{i=1}^{2n}{y}_i{d}_i^2+(1-y_i)\max (margin-d_i,0{)}^2$$ 其中，$y_i$为第$i$个样本是否相似的标签，$d_i$为第$i$个样本之间的距离，$margin$为边际值，是一个预先设定的阈值，通常表示相似度的界限。

适用于相似度度量问题，目标是鼓励相似样本之间的距离尽量小，不相似样本之间的距离尽量大。与Triplet损失类似，都是通过比较样本之间的距离来进行相似度度量，但是Triplet损失计算三元组样本之间的距离，而对比损失计算二元组样本之间的距离。

假设我们要训练一个人脸识别模型，给定一张人脸图片，模型需要判断它是否属于某个人。我们可以将每张人脸图片输入到模型中，模型会输出一个表示人脸特征的向量。如果两张人脸属于同一个人，它们的特征向量应该比较接近；如果两张人脸属于不同的人，它们的特征向量应该比较远离。因此，我们可以使用对比损失来衡量两个特征向量之间的相似度或差异度。

当$y_i=0$时，表示第$i$个样本对应的标签不相同，因此损失函数的第一项为$d_i^2$；当$y_i=1$时，表示第$i$个样本对应的标签相同，因此损失函数的第二项为$\max (m-d_i,0{)}^2$。通过调整阈值$m$，我们可以控制模型对相似度的敏感度。

具体来说，当$m$较大时，模型对相似度的敏感度较低，即模型更倾向于将距离较远的样本视为不相似；当$m$较小时，模型对相似度的敏感度较高，即模型更倾向于将距离较近的样本视为相似。因此，通过适当调整阈值$m$，可以使模型更加准确地判断两个样本之间的相似性或差异性，提高模型的分类性能。

在训练过程中，我们将每个样本的对比损失累加起来，得到整个训练集上的平均损失，作为模型的性能指标。通过不断迭代，我们可以让模型逐渐学习到更好的特征表示，提高人脸识别的准确率。相比于交叉熵损失函数，对比损失函数更适用于度量两个向量之间的相似度或差异度，因此广泛应用于人脸识别、图像检索等领域。

余弦相似度损失（Cosine Similarity Loss）

$$L=\frac{1}{n}\sum _{i=1}^n(1-\cos ({\theta }_i))$$ 其中，${\theta }_i$为第$i$个样本之间的夹角，$n$为样本数。

适用于相似度度量问题，目标是鼓励相似样本之间的余弦相似度尽量接近1。与对比损失、Triplet损失不同，余弦相似度损失计算样本之间的余弦相似度，而不是距离。

交叉熵损失加权的Dice损失（Dice Loss）

$$L=-\frac{1}{n}\sum _{i=1}^n\frac{2{\sum }_j^m{y}_{ij}\widehat{y_{ij}}+c}{{\sum }_j^m{y}_{ij}+{\sum }_j^m\widehat{y_{ij}}+c}$$ 其中，$y_{ij}$为第$i$个样本的第$j$个类别的真实标签，$\widehat{y_{ij}}$为第$i$个样本的第$j$个类别的预测值，$n$为样本数，$m$为类别数，$c$为平滑系数。

适用于图像分割问题，目标是最大化预测结果与真实结果之间的重叠部分。与交叉熵损失不同，Dice损失不考虑类别之间的关系，只关注预测结果与真实结果的重叠部分。

在图像分割中，我们需要将图像中的每个像素分配到不同的类别中。对于每个像素，我们可以将其真实标签表示为一个one-hot编码的向量，其中第$i$个位置表示该像素属于第$i$个类别的概率。类似地，模型的预测标签也可以表示为一个one-hot编码的向量。我们可以将真实标签和预测标签之间的Dice系数定义为：
$$Dice=\frac{2|X\cap Y|}{|X|+|Y|}$$
其中，$X$和$Y$分别表示真实标签和预测标签的二进制掩码，$|\cdot |$表示掩码中1的个数。Dice系数的取值范围为0到1，其中0表示完全不匹配，1表示完全匹配。
为了将Dice系数转化为损失函数，我们可以将其转化为1-Dice系数的形式，即：
$$Dic{e}_{l}oss=1-Dice$$
这样做的好处是，当Dice系数越大时，Dice Loss越小，因此模型的训练目标就是最小化Dice Loss，从而提高Dice系数，进而提高图像分割的准确率。
需要注意的是，Dice Loss并不是一个凸函数，因此在优化过程中可能会陷入局部最优解。为了避免这种情况，通常我们会使用一些正则化技术，如L1或L2正则化，或者使用其他的优化算法，如Adam等。

Triplet损失（Triplet Loss）

$$L=\max (0,d_{a,p}-d_{a,n}+margin)$$ 其中，$d_{a,p}$为锚点样本和正样本之间的距离，$d_{a,n}$为锚点样本和负样本之间的距离，$margin$为边际值。

适用于人脸识别等问题，目标是通过比较同一人的不同照片之间的距离与不同人之间的距离，鼓励同一人的照片之间的距离尽量小，不同人之间的距离尽量大。与对比损失类似，都是通过比较样本之间的距离来进行相似度度量，但是Triplet损失计算三元组样本之间的距离，而对比损失计算二元组样本之间的距离。

在三元组损失（Triplet Loss）中，锚点样本是指我们希望学习相似度的样本。具体来说，我们将每个样本表示为一个向量，通过计算向量之间的距离来衡量它们之间的相似度。在三元组损失中，我们将每个样本分为三个部分：锚点样本、正样本和负样本。其中，锚点样本是我们希望学习相似度的样本，正样本是和锚点样本属于同一类别的样本，负样本是和锚点样本属于不同类别的样本。
具体来说，对于每个锚点样本$a$，我们需要找到一个正样本$p$和一个负样本$n$，使得锚点样本和正样本的距离比锚点样本和负样本的距离更小。这样做的目的是使得同类别的样本之间的距离更近，不同类别的样本之间的距离更远，从而提高相似度学习的效果。因此，三元组损失的计算公式可以表示为：
$$L=max(d(a,p)-d(a,n)+m,0)$$
其中，$d(a,p)$表示锚点样本$a$和正样本$p$之间的距离，$d(a,n)$表示锚点样本$a$和负样本$n$之间的距离，$m$是一个超参数，表示margin，用于控制锚点样本和正负样本之间的距离差。如果$d(a,p)-d(a,n)+m>0$，则损失为正，表示模型需要调整参数以使得$d(a,p)-d(a,n)+m$尽可能小；否则损失为0，表示模型已经满足要求，不需要再调整参数了。
需要注意的是，在实际应用中，我们通常会选择一些具有代表性的锚点样本，如每个类别中的中心样本或者一些难以分类的样本，以提高相似度学习的效果。同时，我们也可以使用一些技巧，如在线挖掘（online mining）或离线挖掘（offline mining），来选择合适的正负样本，从而进一步提高模型的性能。

Focal Loss(基于2分类，可推广至多分类)

Focal Loss是一种针对类别不平衡问题（class imbalance）的损失函数，在目标检测和图像分割等任务中被广泛使用。它的主要思想是对于难以分类的样本（即预测概率接近0或1的样本）给予更大的权重，从而集中优化这些难以分类的样本。下面我们通过一个例子来说明Focal Loss是如何起作用的。
假设我们有一个二分类问题，其中正样本和负样本的分布比例为1:9。我们使用交叉熵（Cross-Entropy）作为损失函数进行训练，但是由于负样本的数量过多，模型很容易过度关注负样本，而忽略了正样本。此时，我们可以使用Focal Loss来解决这个问题。

Focal Loss（α变体）的计算公式为，引入α系数，解决表示正负样本数量平衡问题：
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$
其中，$p_t$表示模型预测样本属于正类别的概率，${\alpha }_t$是一个权重系数，用于平衡正负样本的数量，$\gamma$是一个调节参数，用于控制难易样本的权重。在二分类问题中，我们可以将${\alpha }_t$定义为：
$${\alpha }_t=\{\begin{array}{ll}\alpha ,& \text{if }y=1\\ 1-\alpha ,& \text{if }y=0\end{array}$$
其中，$y$表示样本的真实标签，$\alpha$是一个超参数，用于平衡正负样本的数量。在实践中，通常将$\alpha$设置为正样本的比例，即$\alpha =0.1$，在上面的例子中就是0.1。

接下来，我们来看看$\gamma$的作用。当$\gamma =0$时，Focal Loss退化为标准的交叉熵损失函数；当$\gamma >0$时，对于易于分类的样本，$\gamma$的增加会使得损失函数的权重变小，从而减少模型对易于分类的样本的关注；而对于难以分类的样本，$\gamma$的增加会使得损失函数的权重变大，从而集中优化难以分类的样本。因此，通过调节$\gamma$的大小，我们可以控制模型对不同难易程度的样本的关注程度。

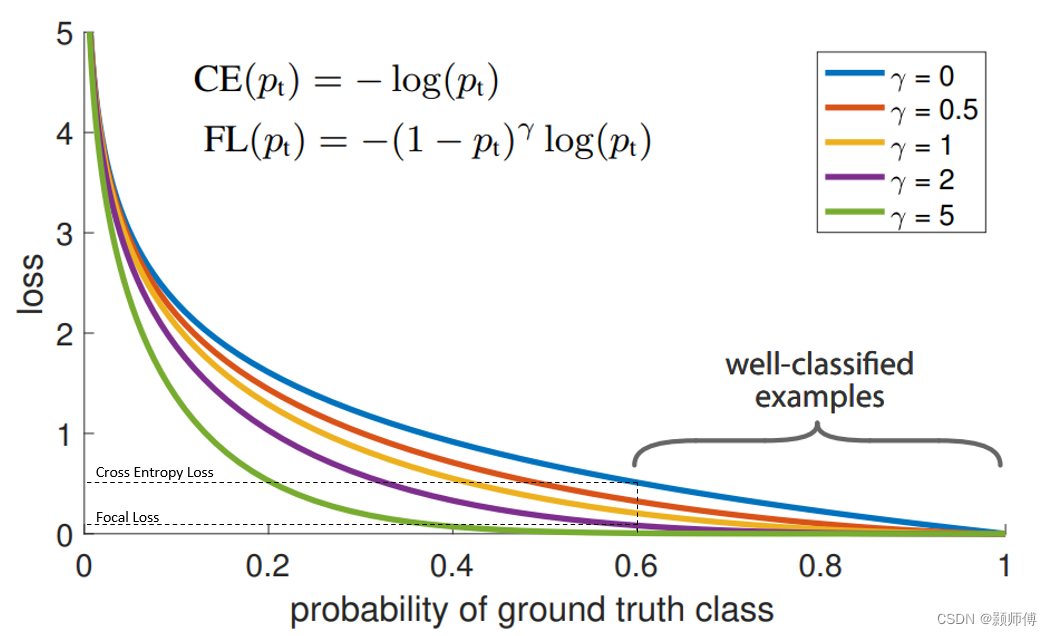
如图所示，易分样本虽然loss少，但数量很多，引入平衡系数后，降低了这部分loss，而对于难分样本，$p_t$接近0，对损失影响并不大。

总之，Focal Loss的主要作用是对于难以分类的样本给予更大的权重，从而集中优化难以分类的样本。在目标检测和图像分割等任务中，由于正负样本比例的巨大差异，Focal Loss可以帮助我们更好地平衡正负样本的数量，从而提高模型的性能。

相关的pytorch代码：

class WeightedFocalLoss(nn.Module):
    "Non weighted version of Focal Loss"    
    def __init__(self, alpha=.25, gamma=2):
            super(WeightedFocalLoss, self).__init__()        
            self.alpha = torch.tensor([alpha, 1-alpha]).cuda()        
            self.gamma = gamma
            
    def forward(self, inputs, targets):
            BCE_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction='none')        
            targets = targets.type(torch.long)        
            at = self.alpha.gather(0, targets.data.view(-1))        
            pt = torch.exp(-BCE_loss)        
            F_loss = at*(1-pt)**self.gamma * BCE_loss        
            return F_loss.mean()