基础排序算法【归并排序+非递归版本+边界修正】
- Ⅰ.归并排序(递归版本)
- ①.分割
- ②.归并
- ③.拷贝
- Ⅱ.非递归版本
- Ⅲ.边界修正
Ⅰ.归并排序(递归版本)
递归排序,采用的是分治法。分成子问题来处理。先让序列不断分割成子序列,当子序列有序后再合并。
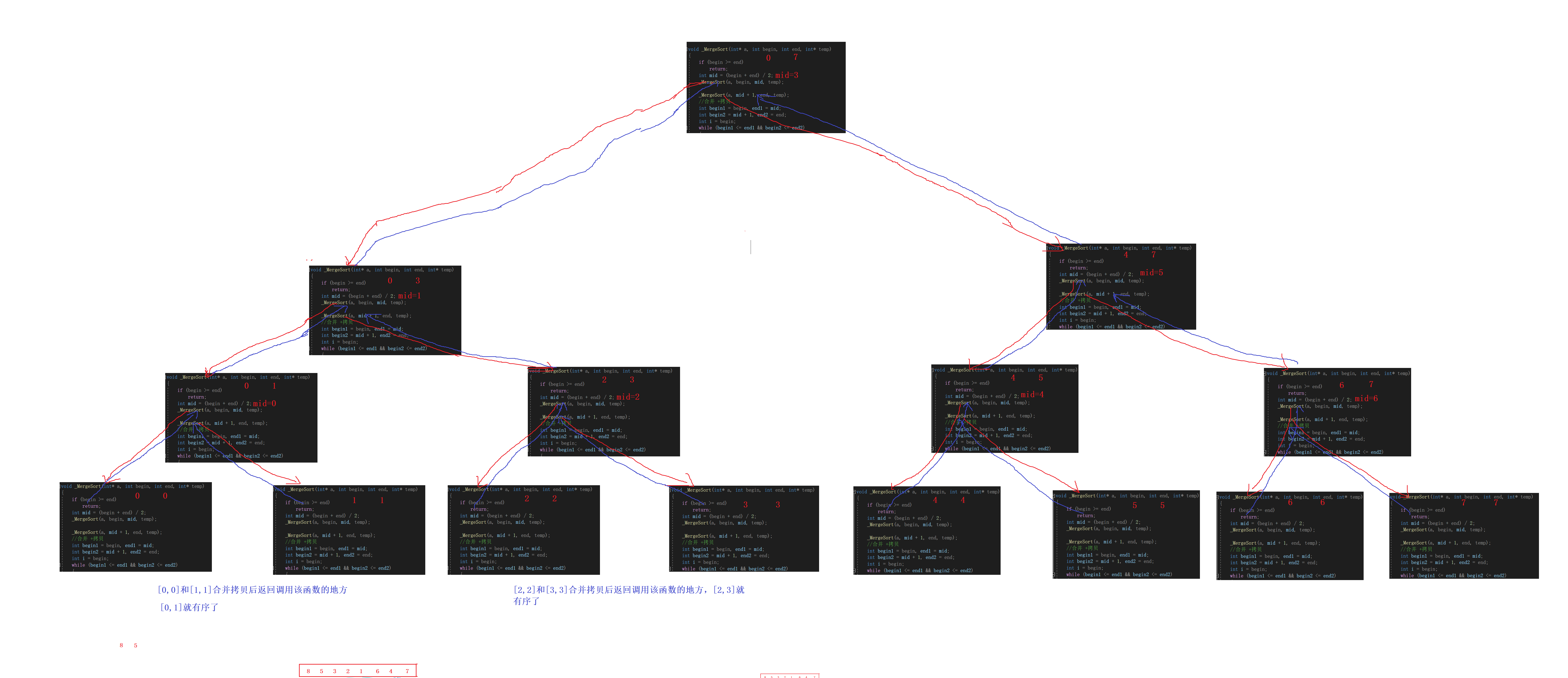
对于一段序列,分割成左右子序列,再对左序列进行不断分割(左序列又形成左右序列……),直到无法分割为止,开始进行合并,将分割的子序列合并成有序序列。当左序列合并完后,右序列再开始不断分割,当右序列分割完进行合并,合并完,右序列也就有序了,左右序列再合并。最终形成一个有序序列。
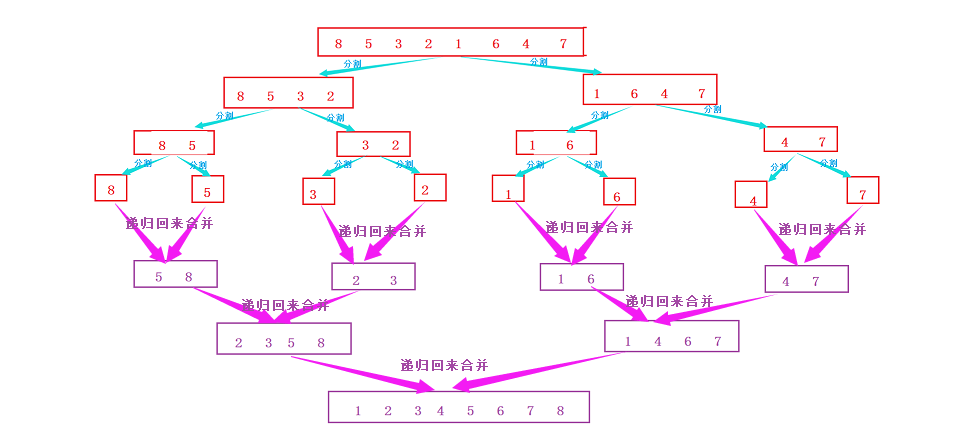
递归展开图分析:
注意:因为合并有序序列需要用到新的数组,所以需要动态开辟一个。但不能在含递归的函数中使用,不然就不断的开辟空间了,所以需要另一个函数来作为支架,来提供temp数组。
void MergeSort(int* a, int n)
{
int a[] = { 8,6,4,5,3,2,7,1 };
int n = sizeof(n) / sizeof(a[0]);
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc");
}
_MergeSort(a, 0, n - 1, temp);
}
```cpp
void _MergeSort(int* a, int begin, int end, int* temp)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, temp);
_MergeSort(a, mid + 1, end, temp);
//将[begin mid] 和[mid+1 end]合并成一个有序序列
int begin1 = begin, end1 = mid;
int begin2 = mid + 1,end2 = end;
int i = begin;
//合并两个有序序列的常用方法
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));
}
①.分割
第一步首先对该序列进行分割,从哪分割呢?当然从中间分割。
利用递归来实现不断的分割,直到无法分割为止。
void _MergeSort(int* a, int begin, int end, int* temp)
{
1.//当无法分割时,开始返回。
if (begin >= end)
return;
2.//进行分割
int mid = (begin + end) / 2;
//[begin mid][mid+1 end]
//不断的分割直到分成一个有序序列时
_MergeSort(a, begin, mid, temp);
//将左区间不断分割
_MergeSort(a, mid + 1, end, temp);
//将右区间不断分割
//走到这里表明左右小序列是一个有序序列了
//接下来就是合并有序序列了
//将[begin mid] 和[mid+1 end]合并成一个有序序列
}
②.归并
归并思想很简单,就是让两个有序序列进行比较,较小的值先放入新开辟的数组temp里,较小数组的下标要++,然后再进行比较,重复这个操作,直到某一个序列被全部放入数组中。
接下来,肯定有一个数组没有全部放入,但不知道哪一个,需要进行讨论,直接将没有放空的序列直接尾插到数组temp后面即可。
//将[begin mid] 和[mid+1 end]合并成一个有序序列
int begin1 = begin, end1 = mid;
int begin2 = mid + 1,end2 = end;
int i = begin;
//合并两个有序序列的常用方法
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];//将较小的值放入temp中
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)//直接将没有放空的序列尾插到temp数组后面即可。
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)//因为不知道是哪一个没有被放空,需要讨论一下哪个序列还有数值。
{
temp[i++] = a[begin2++];
}
③.拷贝
最后直接temp数组中的值再拷贝会a数组中就完成了a数组的排序。
可以使用memcpy函数进行拷贝。
memcpy(目的空间,源空间,大小);
memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));
//这里必须要加上begin,因为不一定从第一个位置开始,也可能从中间开始拷贝回去。
Ⅱ.非递归版本
我们可以采取非递归的方式来实现归并排序。因为我们知道归并的思想就是将多个有序序列合并成一个有序序列。
而递归实现的版本就是将没有序的序列分割成有序的序列,然后再进行合并,我们可以不用递归分割,直接就可以得到有序序列,因为一个序列肯定是有序的,所以我们直接可以从一个有序序列和一个有序序列开始合并,然后再根据得到的有序序列进行二二合并……。
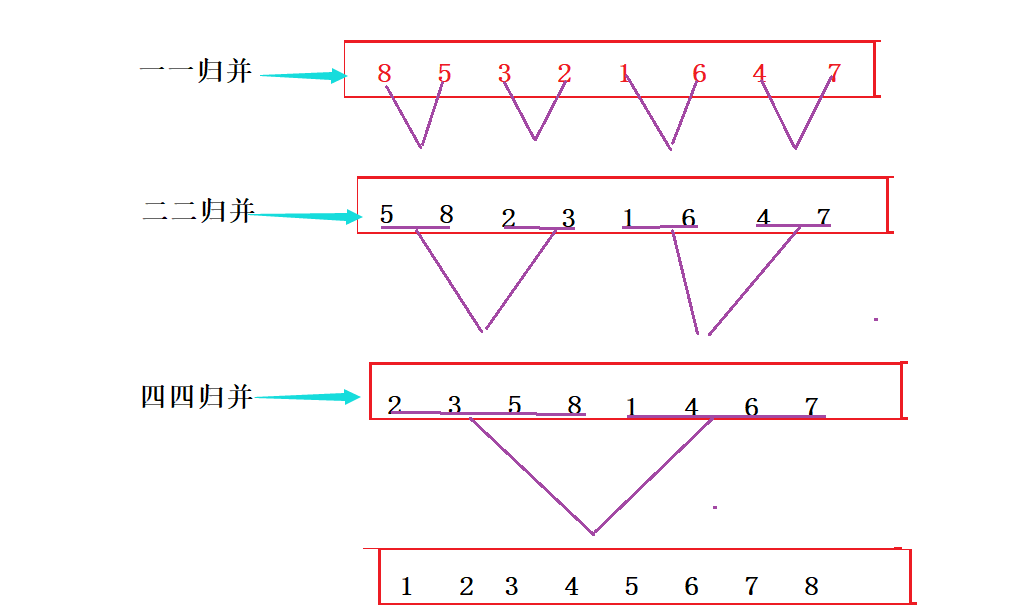
这里的难点就在于边界的控制,怎么控制每次要合并的序列的边界呢?
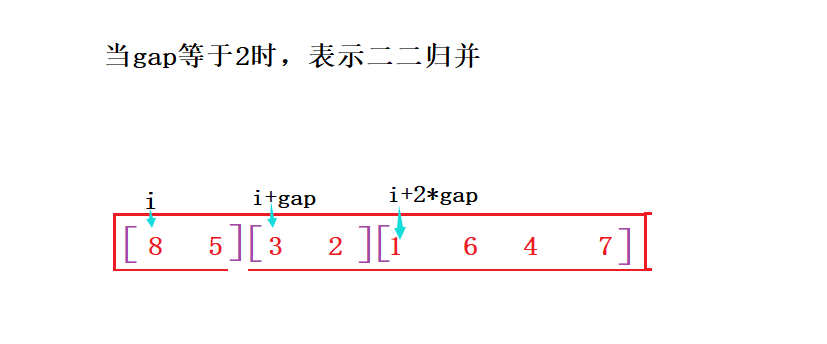
这里我定义一个gap,这个变量代表着每次合并序列的个数。
找到边界的规律最好的方式是画图。
i就是每次要归并的起始位置。
因为每次归并的个数是gap个,所以i每次要跳过2gap个单位。
begin1就是i的位置,end1应该是i+gap位置,但是数组下标要减一。
i+gap表示end1后面的位置也就是begin2了。而end2其实就是下一次开始位置的前面,下一次要跳过2gap位置,所以end2的位置为i+2*gap-1;
int gap = 1;
//gap是表示每次归并的个数
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
}
如何控制让每次归并的个数呢?只要让gap每次两倍的增长就可以了,归并一次,gap增长一倍,当gap=n/2时,再归并就可以结束了。
int gap = 1;
//gap是表示每次归并的个数
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
}
gap *= 2;//每次归并完后,gap增长一倍。
}
这只是完成归并部分,还有拷贝操作没有实现,不过先不急,我们先研究一下这个归并操作有何bug。
bug:这种归并只能对于2^次方个数有用,而对于不是2的次方时,就会存在越界,因为gap每次都是增长一倍,那么边界的范围也就确定下来了,一旦序列没有2的次方个时那么就会存在要合并的两个序列区间会越界。
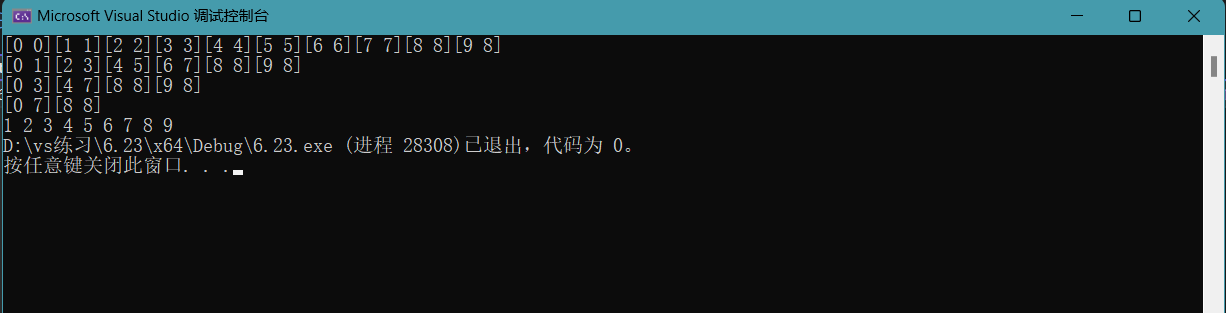
我们可以演示一下打印出来看下。给9个数据。
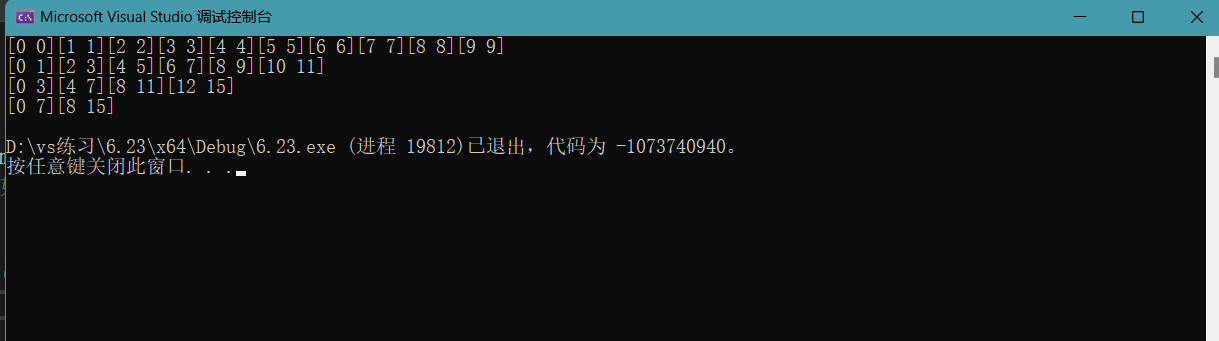
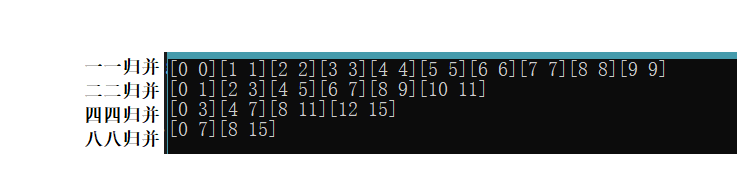
九个数据,最大的下标也就是8。所以超过8的都会越界。
begin1是永远不可能越界的,因为begin1就是i,而i是小于n的。
end2和begin2,end2会越界。
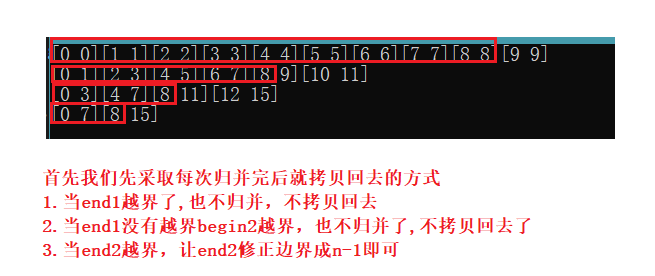
这里我们采用一般的拷贝方式,就是部分拷贝,归并完后就拷贝回去,而不是当全部归并后再拷贝回去。
存在三种情况:
1.当end1越界时,end1后面的肯定都越界了。那后面的我们就不要归并了,不要归并也就意味着也不用拷贝。只需要将前面的归并然后再拷贝回去。
2.当end1没有越界,begin2越界了,跟上面类似,begin2越界了,那后面就不用再归并了,不用拷贝了。
3.当end2越界了,那我们只需要将end2修改成n-1即可。
//非递归形式的归并算法
void _MergeSortNor(int* a, int n, int* temp)
{
int gap = 1;
//gap是表示每次归并的个数
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
if (end1 >= n )
{
break;
}
if (begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
printf("[%d %d][%d %d]", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
memcpy(a + i, temp + i, sizeof(int)*(end2 - i + 1));
//有两种拷贝方式 ,1,直接等全部归并完后一把梭哈,或者是归并完一次就拷贝回去
//归并一部分拷贝一部分
}
gap *= 2;
}
}
Ⅲ.边界修正
而另一种拷贝方式就是全部归并完后再拷贝回去。
这种方法很折磨人,因为涉及复杂的边界修正。这里不推荐使用。
不能像上面的直接break,一定要将数据弄下来,因为这是一把拷贝过去的,如果遇到越界的那break后,可能有的数据没有进入temp数组里面,那temp数组再拷贝给a数组,这不扯谈嘛。
要保证每次归并的数据是有效的。
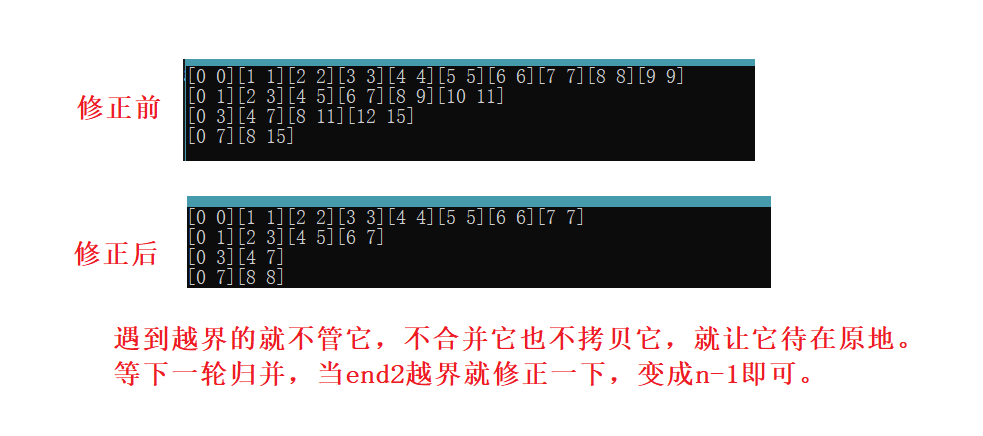
所以正因为这里的拷贝是一把梭哈,所以我们必须要进行边界修正处理。当end1,begin2,或end2出现越界了,就要修改它的边界。
有人这样修改,对吗?
很明显是不对的。不可以全部都变成n-1,因为这样会将最后一个数字多归并一次。
//当end1越界时
if (end1 >= n)
{
end1 = n - 1;
begin2 = n - 1;
end2 = n - 1;
}
正确的修正是让第二个区间不存在,那么下面的合并操作就不会进去。
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;//将第二个区间修正成不存在就可以了
end2 = n - 1;
}
当begin2越界时,前面的[begin1,end1]是正常的,要进行归并,而后面就不需要了,所以直接让后面的区间变成不存在的就可以不进入归并操作。
if (begin2 >= n)
{
begin2 = n;//将区间修正成不存在就可以了
end2 = n - 1;
}
当end2越界时,也就是前面的[begin1,end1],begin2没有越界,这时只需要将end2修正一下就可以了。
if (end2 >= n)
{
end2=n-1;
}
void _MergeSortNor(int* a, int n, int* temp)
{
int gap = 1;
//gap是表示每次归并的个数
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n)
{
end2 = n - 1;
}
printf("[%d %d][%d %d]", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
}
memcpy(a,temp,sizeof(int)*n);
//如果采用一把梭哈的方法,那必须采取纯修正路线
gap *= 2;
printf("\n");
}
}
int main()
{
int* temp = (int*)malloc(sizeof(int) * 9);
if (temp == NULL)
{
perror("malloc");
}
int a[] = { 8,6,4,5,3,2,7,1, 9};
_MergeSortNor(a, 9,temp);
for (int i = 0; i < 9; i++)
{
printf("%d ", a[i]);
}
}