计算机基础---＞数据结构（3）【堆（超详细）】

news2024/11/20 12:30:42

文章目录

  • 堆
  • 堆的时间复杂度
  • 堆的分类
  • 堆的存储
  • 堆的操作
    • 插入元素
    • 删除堆顶元素
  • 堆排序
    • 建堆
    • 排序
  • 所有操作代码

堆

堆一般分为两种类型：最大堆和最小堆。在最大堆中，父节点的值总是大于或等于子节点的值，而在最小堆中，父节点的值总是小于或等于子节点的值。堆可以被用来进行排序，如堆排序，它的时间复杂度是 O(nlogn)。堆还可以被用来实现优先级队列、图算法中的最短路径算法、高效的计算中位数等等

堆一般是完全二叉树，但不都是完全二叉树，只是为了方便存储和索引，我们通常用完全二叉树的形式来表示堆，事实上，广为人知的斐波那契堆和二项堆就不是完全二叉树,它们甚至都不是二叉树。

堆的时间复杂度

相较于有序数组，堆的主要优势在于插入和删除数据效率较高。 当只关心所有数据中的最大值或最小值，存在多次取最大值或最小值，多次插入或删除数据时，就可以使用堆。

有序数组堆
初始化O(nlog(n))O(n)
查找最大（最小）值O(n)O(1)
插入（删除）数据O(n)O(log(n))

堆的分类

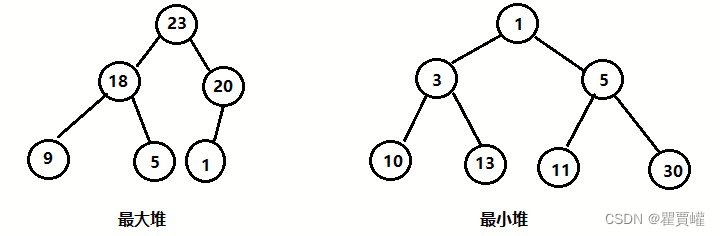
堆分为 最大堆 和 最小堆。二者的区别在于节点的排序方式。

  • 最大堆：堆中的每一个节点的值都大于等于子树中所有节点的值
  • 最小堆：堆中的每一个节点的值都小于等于子树中所有节点的值

在这里插入图片描述

堆的存储

由于完全二叉树的优秀性质，利用数组存储二叉树即节省空间，又方便索引（若根结点的序号为 1，那么对于树中任意节点 i，其左子节点序号为 2*i，右子节点序号为 2*i+1）。

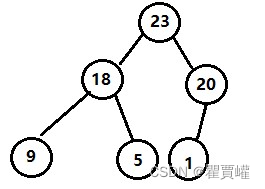
在这里插入图片描述

Index0123456
value231820951

堆的操作

堆的操作主要包括两种：插入元素和删除堆顶元素。

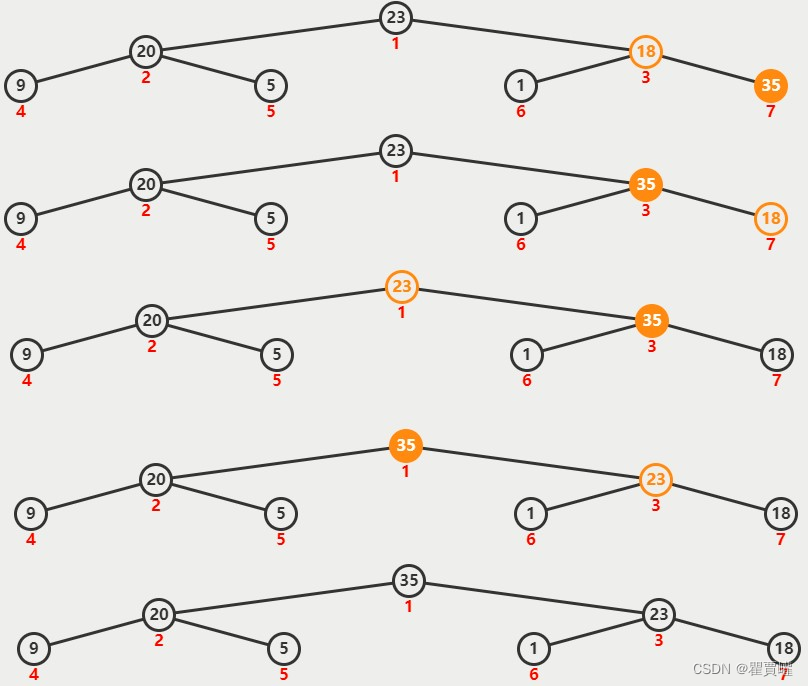
插入元素

  1. 将要插入的元素放到最后
  2. 从底向上，如果父结点比该元素小，则该节点和父结点交换，直到无法交换

在这里插入图片描述

    // 向树中添加元素
    public void add(int val) {
        this.size++;
        this.data[this.size] = val;
//        floatUp();
        floatUp1(val);
    }

    // 上浮操作，交换操作
    private void floatUp() {
        int curIndex = this.size;
        int paintIndex = getParentIndex(curIndex);
        while (curIndex > 1 && this.data[curIndex] > this.data[paintIndex]) {
            swap(curIndex, paintIndex);
            curIndex = paintIndex;
            paintIndex = getParentIndex(curIndex);
        }
    }

    // 上浮操作，替换操作
    private void floatUp1(int ele) {
        int curIndex = this.size;
        int paintIndex = getParentIndex(curIndex);
        while (curIndex > 1 && ele > this.data[paintIndex]) {
            this.data[curIndex] = this.data[paintIndex];
            curIndex = paintIndex;
            paintIndex = getParentIndex(curIndex);
        }
        this.data[curIndex] = ele;
    }

删除堆顶元素

自底向上堆化

  1. 将堆顶元素删除
  2. 然后比较左右子结点，将较大的元素填充到根节点的位置
  3. 一直循环填充空出的位置，直到堆的最底部

会出现空节点，浪费存储空间

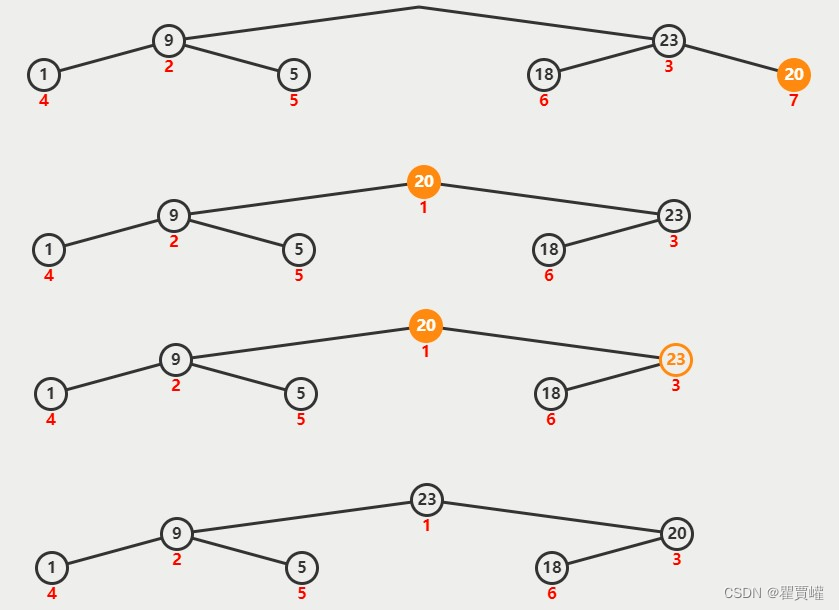
自顶向下堆化

  1. 将堆顶元素删除
  2. 将堆尾元素放到堆顶
  3. 判断堆顶元素和左右子结点，将较大的元素与堆顶元素交换
  4. 一直循环直至堆的最底部

在这里插入图片描述

    // 从堆中取出优先级最大的元素
    public int removeMaxValueFromHeap() {
        int result = this.data[1];
        this.data[1] = this.data[size];
        this.size--;

        int curIndex = 1;
        int leftChildIndex = getLeftChild(curIndex);
        while (leftChildIndex <= this.size) {
            int rightChildIndex = leftChildIndex + 1;

            // 判断右子树是否存在并且右子树要大于左子树，否则就是左子树与父结点进行判断
            if (rightChildIndex <= this.size && this.data[leftChildIndex] < this.data[rightChildIndex]) {
                swap(rightChildIndex, curIndex);
                curIndex = rightChildIndex;
            } else {
                if (this.data[leftChildIndex] > this.data[curIndex]) {
                    swap(leftChildIndex, curIndex);
                }
                curIndex = leftChildIndex;
            }
            leftChildIndex = getLeftChild(curIndex);
        }
        return result;
    }

堆排序

  1. 建堆，将一个无序的数组建立为一个堆
  2. 排序，将堆顶元素取出，对剩余元素进行堆化，直到所有元素被取出

建堆

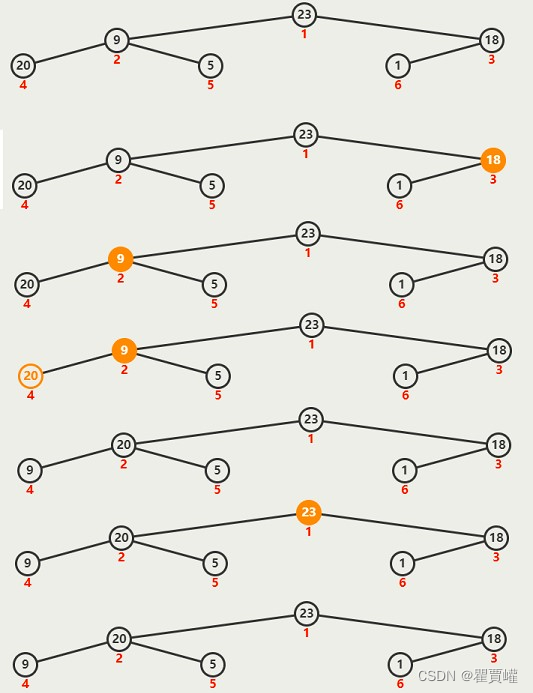
建堆的过程就是一个对所有非叶节点的自顶向下堆化的过程。非叶节点就是最后一个节点的父结点以及它之前的元素都是非叶节点。也就是，如果节点个数为n，我们需要对n/2到1的节点进行自顶向下堆化。

在这里插入图片描述

    public MaxHeap(int[] arr) {
        this.data = new int[arr.length + 1];
        this.size = arr.length;
        for (int i = 0; i < arr.length; i++) {
            this.data[i + 1] = arr[i];
        }
        for (int i = this.size / 2; i > 0; i--) {
            sinkDown(i);
        }
    }
        // 从节点为index处开始下沉
    private void sinkDown(int index) {
        int curIndex = index;
        int leftChildIndex = getLeftChild(curIndex);
        while (leftChildIndex <= this.size) {
            int rightChildIndex = leftChildIndex + 1;

            // 判断右子树是否存在并且右子树要大于左子树，否则就是左子树与父结点进行判断
            if (rightChildIndex <= this.size && this.data[leftChildIndex] < this.data[rightChildIndex]) {
                swap(rightChildIndex, curIndex);
                curIndex = rightChildIndex;
            } else {
                if (this.data[leftChildIndex] > this.data[curIndex]) {
                    swap(leftChildIndex, curIndex);
                }
                curIndex = leftChildIndex;
            }
            leftChildIndex = getLeftChild(curIndex);
        }
    }

排序

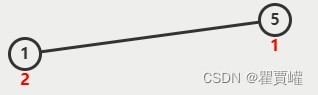
由于堆顶元素是所有元素中最大的，所以我们重复取出堆顶元素，将这个最大的堆顶元素放至数组末尾，并对剩下的元素进行堆化即可。由于堆尾元素空出来了，我们就可以将取出的元素放在末尾，所以其实就是做了一次交换操作。

在这里插入图片描述

Index0123456
value232018951

在这里插入图片描述

Index0123456
value209181523

在这里插入图片描述

Index0123456
value189512023

在这里插入图片描述

Index0123456
value915182023

在这里插入图片描述

Index0123456
value519182023

在这里插入图片描述

Index0123456
value159182023

所有操作代码

package datastructure.heap;

import java.util.*;

public class MaxHeap {

    private int[] data; // 保存树中的节点值
    private int size; // 保存树中的节点个数

    public MaxHeap() {
        this.data = new int[500];
        Arrays.fill(data, Integer.MIN_VALUE);
        this.size = 0;
    }

    public MaxHeap(int[] arr) {
        this.data = new int[arr.length + 1];
        this.size = arr.length;
        for (int i = 0; i < arr.length; i++) {
            this.data[i + 1] = arr[i];
        }
        for (int i = this.size / 2; i > 0; i--) {
            sinkDown(i);
        }
    }

    // 判断堆是否为空
    public boolean isEmpty() {
        return this.size == 0;
    }

    // 获取堆中元素个数
    public int getSize() {
        return this.size;
    }

    // 根据当前节点所在数组的索引获取父结点的索引
    public int getParentIndex(int index) {
        if (index == 0) {
            return -1;
        }
        return index / 2;
    }

    // 根据当前节点所在数组的索引获取左孩子节点的索引
    public int getLeftChild(int index) {
        return index * 2;
    }

    // 向树中添加元素
    public void add(int val) {
        this.size++;
        this.data[this.size] = val;
//        floatUp();
        floatUp1(val);
    }

    // 上浮操作，交换操作
    private void floatUp() {
        int curIndex = this.size;
        int paintIndex = getParentIndex(curIndex);
        while (curIndex > 1 && this.data[curIndex] > this.data[paintIndex]) {
            swap(curIndex, paintIndex);
            curIndex = paintIndex;
            paintIndex = getParentIndex(curIndex);
        }
    }

    // 上浮操作，替换操作
    private void floatUp1(int ele) {
        int curIndex = this.size;
        int paintIndex = getParentIndex(curIndex);
        while (curIndex > 1 && ele > this.data[paintIndex]) {
            this.data[curIndex] = this.data[paintIndex];
            curIndex = paintIndex;
            paintIndex = getParentIndex(curIndex);
        }
        this.data[curIndex] = ele;
    }


    // 获取堆中最大元素
    public int getMaxValueFromHeap() {
        if (isEmpty()) {
            return -1;
        }
        return this.data[1];
    }

    // 从堆中取出优先级最大的元素
    public int removeMaxValueFromHeap() {
        int result = this.data[1];
        this.data[1] = this.data[size];
        this.size--;

        int curIndex = 1;
        sinkDown(curIndex);
        return result;
    }

    // 从节点为index处开始下沉
    private void sinkDown(int index) {
        int curIndex = index;
        int leftChildIndex = getLeftChild(curIndex);
        while (leftChildIndex <= this.size) {
            int rightChildIndex = leftChildIndex + 1;

            // 判断右子树是否存在并且右子树要大于左子树，否则就是左子树与父结点进行判断
            if (rightChildIndex <= this.size && this.data[leftChildIndex] < this.data[rightChildIndex]) {
                swap(rightChildIndex, curIndex);
                curIndex = rightChildIndex;
            } else {
                if (this.data[leftChildIndex] > this.data[curIndex]) {
                    swap(leftChildIndex, curIndex);
                }
                curIndex = leftChildIndex;
            }
            leftChildIndex = getLeftChild(curIndex);
        }
    }

    // 交换的方法
    private void swap(int curIndex, int changeIndex) {
        int temp = this.data[curIndex];
        this.data[curIndex] = this.data[changeIndex];
        this.data[changeIndex] = temp;
    }

    @Override
    public String toString() {
        StringBuffer sb = new StringBuffer("[");
        for (int i = 0; i < this.size; i++) {
            if (i == 0) {
                sb.append(this.data[i + 1]);
            } else {
                sb.append(", " + this.data[i + 1]);
            }

        }
        sb.append("]");
        return sb.toString();
    }

    public static void main(String[] args) {
        int[] arr = new int[]{23, 9, 20, 18, 5, 1};
        System.out.println("数组中的元素：" + Arrays.toString(arr));
        MaxHeap maxHeap = new MaxHeap(arr);
//        Arrays.stream(arr).forEach(maxHeap::add);
        // 将数组变为堆
        System.out.println("创建堆：" + maxHeap.toString());

        // 向堆中添加元素
        maxHeap.add(35);
        System.out.println("向堆中添加元素35：" + maxHeap.toString());

        // 删除堆顶元素
        maxHeap.removeMaxValueFromHeap();
        System.out.println("删除堆顶元素：" + maxHeap.toString());

        // 堆排序
        for (int i = 0; i < arr.length; i++) {
            arr[i] = maxHeap.removeMaxValueFromHeap();
        }
        System.out.println("堆排序：" + Arrays.toString(arr));
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/680667.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

计算机自我介绍500字范文（合集）

计算机自我介绍500字范文（合集）

计算机自我介绍500字范文1 本人是___大学计算机系统维护专业的学生。大学四年的学习&#xff0c;积累了丰富的专业知识&#xff0c;广泛的人际关系&#xff0c;培养我成为一个敢于承担责任&#xff0c;对待生活乐观积极&#xff0c;吃苦耐劳的青年。在专业方面我的主攻方向是计…
阅读更多...
Ffmpeg6.0版本源码解读第一期！

Ffmpeg6.0版本源码解读第一期！

前言&#xff1a; 大家好&#xff0c;最近一直在直播讲解Ffmpeg6.0版本的源码解析&#xff0c;这里要明白学习源码能给我们带来什么好处&#xff1f;我相信很多小伙伴已经用过Ffmpeg去开发&#xff0c;不知道大家有没有在开发的过程&#xff0c;调用接口的时候&#xff0c;是否…
阅读更多...
PowerDesigner面向对象建模-常用UML图

PowerDesigner面向对象建模-常用UML图

1 PowerDesigner简介 PowerDesigner最初由Xiao-Yun Wang&#xff08;王晓昀&#xff09;在SDP Technologies公司开发完成。PowerDesigner是Sybase的企业建模和设计解决方案&#xff0c;采用模型驱动方法&#xff0c;将业务与IT结合起来&#xff0c;可帮助部署有效的企业体系架…
阅读更多...
python熟悉python基础语法，了解html网络结构，了解json格式数据，含有字符串

python熟悉python基础语法，了解html网络结构，了解json格式数据，含有字符串

前言 Python网络爬虫是利用Python编写的程序&#xff0c;通过自动化地访问网页、解析html或json数据&#xff0c;并提取所需信息的技术。下面将详细介绍一些与Python网络爬虫相关的重要知识点。 1、Python基础语法&#xff1a; 变量和数据类型&#xff1a;学习如何声明变量以及…
阅读更多...
使用R语言绘制富集条形图，轻松分析基因表达数据

使用R语言绘制富集条形图，轻松分析基因表达数据

一、引言 富集分析&#xff08;enrichment analysis&#xff09;是一种生物信息学方法&#xff0c;它可以帮助我们识别基因或其他的生物实体在某个特定的类别中过度表示的趋势。通俗来说&#xff0c;富集分析通过将基因分类到特定的集合中&#xff0c;然后根据基因在集合中的分…
阅读更多...
万字长文带你深入理解JavaNIO并手动实现多人聊天室

万字长文带你深入理解JavaNIO并手动实现多人聊天室

NIO 网络编程 代码已同步至GitCode&#xff1a;https://gitcode.net/ruozhuliufeng/java-project.git Java NIO简介 IO概述 ​ IO的操作方式通常分为几种&#xff1a;同步阻塞BIO、同步非阻塞NIO、异步非阻塞AIO。 ​ &#xff08;1&#xff09;在JDK1.4之前&#xff0c;我们…
阅读更多...
哈希表/散列表(HashTable)c++实现

哈希表/散列表(HashTable)c++实现

目录 哈希表实现的思想 除留余数法 哈希冲突 第一种方法&#xff1a;探测法实现哈希表 探测法的思想 结点类 插入数据(insert) 冲突因子 数据扩容 哈希值 插入的代码实现以及哈希类 查找数据(find) 删除数据(erase) 第二种方法&#xff1a;拉链法实现哈希表 …
阅读更多...
Kotlin~迭代器模式

Kotlin~迭代器模式

概念 提供一种遍历集合元素的方法&#xff0c;而不暴露集合内部的实现。 角色介绍 iterator 迭代器接口: 定义访问和遍历集合元素的接口&#xff0c;一般包含next和hasNext方法。concrete iterator 具体迭代器: 实现迭代器接口&#xff0c;迭代器的核心逻辑实现。aggregate …
阅读更多...
极致呈现系列之：Echarts热力图的神奇光晕

极致呈现系列之：Echarts热力图的神奇光晕

目录 什么是热力图热力图的特性及应用场景热力图的特性热力图的应用场景 Echarts中热力图的常用属性vue3中创建热力图 什么是热力图 热力图&#xff08;Heatmap&#xff09;是一种基于颜色映射的数据可视化图表&#xff0c;用于展示数据点的密度和分布情况。它使用不同的颜色强…
阅读更多...
RT-Thread-10-线程优先级翻转

RT-Thread-10-线程优先级翻转

线程优先级翻转 前面讲到信号量和互斥量&#xff0c;二者有些区别&#xff1a; 信号量&#xff0c;可以在任何线程&#xff08;以及中断&#xff09;释放&#xff0c;用于同步&#xff0c;线程只在获得许可时才可以运行&#xff0c;强调的是运行步骤&#xff1b; 互斥量&#…
阅读更多...
科技项目验收测试规范有哪些?

科技项目验收测试规范有哪些?

随着科技的不断发展和进步&#xff0c;越来越多的科技项目被投入使用。为了保证这些科技项目的质量&#xff0c;需要进行验收测试。科技项目验收测试是一项非常重要的工作&#xff0c;其结果对项目的质量和功能正常使用有着直接的影响。本文将就科技项 目验收测试规范和第三方软…
阅读更多...
基于51单片机设计的公交车LED屏

基于51单片机设计的公交车LED屏

一、项目介绍 为了提高公交车站点信息的实时性和准确性，方便乘客及时了解公交车到站信息，从而提高公交出行的便利性和舒适度。传统的公交车到站信息是通过人工喊话或者静态的站牌来实现的，这种方式存在信息不及时、不准确、不方便等问题。当前设计基于STC89C52单片机和MAX7…
阅读更多...
PyQt6中文手册

PyQt6中文手册

PyQt6中文手册 一、PyQt6 简介 最后更新于 2021.04.22 本教程是 PyQt6 的入门教程。本教程的目的是让您开始使用 PyQt6 库。 关于 PyQt6 PyQt6 Digia 公司的 Qt 程序的 Python 中间件。Qt库是最强大的GUI库之一。PyQt6的官网&#xff1a;www.riverbankcomputing.co.uk/new…
阅读更多...
2023年企业应该关注的10种AI攻击类型

2023年企业应该关注的10种AI攻击类型

2023年&#xff0c;热度很高的一个话题莫不是生成式AI和chat GPT了。但是&#xff0c;人工智能&#xff08;AI&#xff09;技术的应用安全威胁都已经开始显现。安全研究人员表示&#xff0c;在AI技术快速应用发展过程中&#xff0c;其安全性也面临诸多挑战。为了防范AI技术大规…
阅读更多...
【C++】哈希unordered系列容器的模拟实现

【C++】哈希unordered系列容器的模拟实现

文章目录 一、哈希表的模拟实现&#xff08;开散列&#xff09;1. 开散列的概念2. 开散列的节点结构3. 开散列的插入删除与查找4. 开散列整体代码实现 二、unordered系列容器的封装实现(开散列)1. 迭代器2. unordered_set和unordered_map的封装实现3. 哈希表整体源码 一、哈希表…
阅读更多...
Jacoco代码覆盖率测试

Jacoco代码覆盖率测试

​欢迎光临我的博客查看最新文章: https://river106.cn 1、简介 JaCoCo(Java Code Coverage)是一个开源的覆盖率工具&#xff0c;它针对的开发语言是java&#xff0c;其使用方法很灵活&#xff0c;可以嵌入到Ant、Maven中。 很多第三方的工具提供了对JaCoCo的集成&#xff0c;…
阅读更多...
Java设计模式之结构型-装饰器模式

Java设计模式之结构型-装饰器模式

目录 一、基本概念 二、角色设计 三、代码实现 四、总结 一、基本概念 装饰器模式是指不必在改变原有的类和不使用继承的情况下&#xff0c;动态扩展一个对象的功能。 二、角色设计 角色描述抽象构件是一个接口或者抽象类&#xff0c;定义我们最核心的对象基础构件抽象构…
阅读更多...
GD32 SPI 查询方式和DMA方式在全双模式下效率区别

GD32 SPI 查询方式和DMA方式在全双模式下效率区别

最近在使用SPI的时候&#xff0c;遇到了一些数据传输效率问题&#xff0c;在此记录自己学习过程。SPI的基础知识这里就不在讲述了&#xff0c;直接分析SPI查询方式和DMA方式的效率问题。这里使用的芯片是GD32F303CC。 SPI以查询方式进行全双工通信 1.查询手册&#xff0c;SPI…
阅读更多...
java——网络编程

java——网络编程

文章目录 网络通信协议1. TCP/IP协议2. HTTP协议 Socket编程1.创建Socket对象2.获取输入输出流3.发送数据4.接收数据5.关闭Socket连接 NIO编程1.创建Channel2.创建Buffer3.从Channel中读取数据4.写入数据到Channel中5.关闭Channel和Stream Java网络编程是使用Java语言实现计算机…
阅读更多...
Spark7-9

Spark7-9

7. Spark中的一些重要概念 7.1 Application 使用SparkSubmit提交的个计算应用&#xff0c;一个Application中可以触发多次Action&#xff0c;触发一次Action产生一个Job&#xff0c;一个Application中可以有一到多个Job 7.2 Job Driver向Executor提交的作业&#xff0c;触发…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023