目录
哈希表实现的思想
除留余数法
哈希冲突
第一种方法:探测法实现哈希表
探测法的思想
结点类
插入数据(insert)
冲突因子
数据扩容
哈希值
插入的代码实现以及哈希类
查找数据(find)
删除数据(erase)
第二种方法:拉链法实现哈希表
结点类
哈希类的成员
插入(insert)
扩容
插入数据
插入代码总结:
查找(find)
删除数据(erase)
删除代码总结:
哈希表实现的思想
除留余数法
哈希表的实现方法是通过每个值映射出一个下标位置,再存储到一个数组中的下标所对应的位置(有点类似计数排序)
这个值我们叫做哈希值
如图:我们有一个数组

假如我们此时插入一个14,那么直接映射到数组对应下标即可,此时哈希值也为14
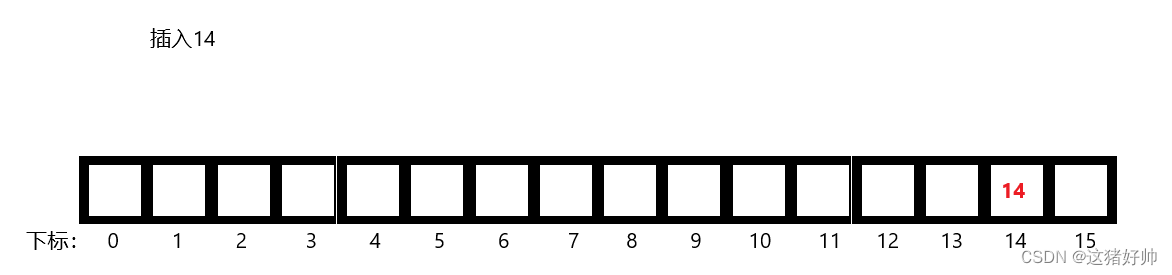
如图数组中通过这种直接映射的方法我们可以直接存储哈希值为0-15的数据,并且数据所对应的哈希值就是它本身
但如果我们此时要在数组中存储一个大于15的数据(例如50)怎么办呢?
解决方法也很简单,前文中哈希值等于数据本身,那么我们此时让数据除(%)数组大小,而余下来的数据就为它的哈希值
如图我们在数组中插入一个50
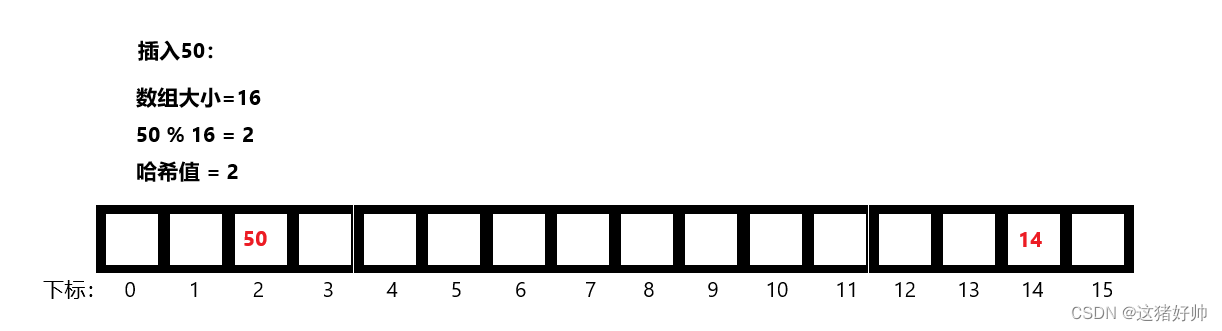
这种方法我们叫做除留余数法
哈希冲突
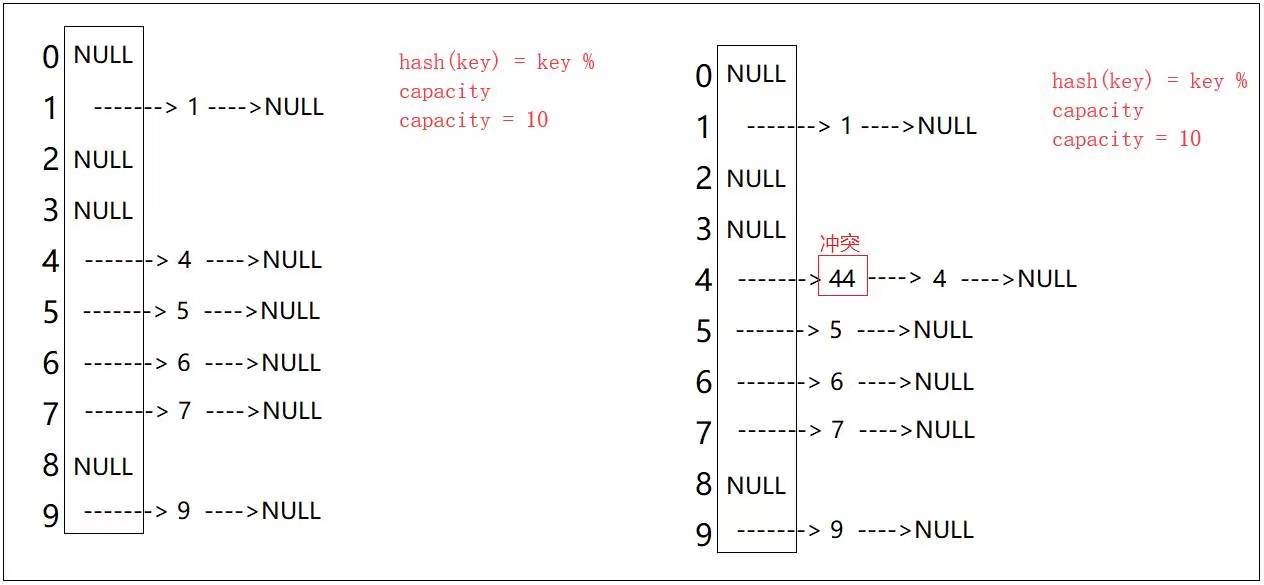
如图数组

我们分别使用除留余数法插入两个数组(0和16)试试
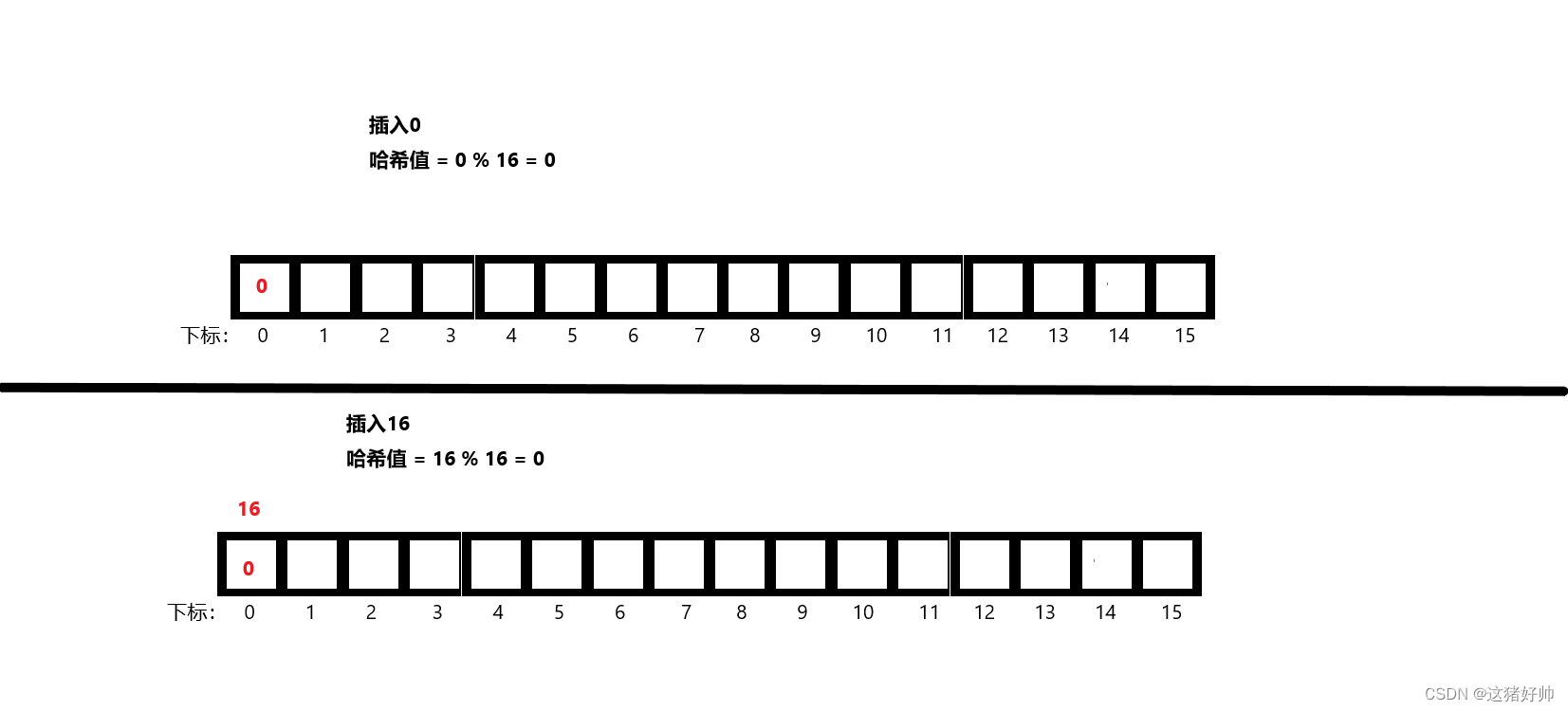
可以看到,此时0和16的哈希值冲突了,这也就是所谓的哈希冲突
而以下说的两种方法都是为了解决哈希冲突
第一种方法:探测法实现哈希表
探测法的思想
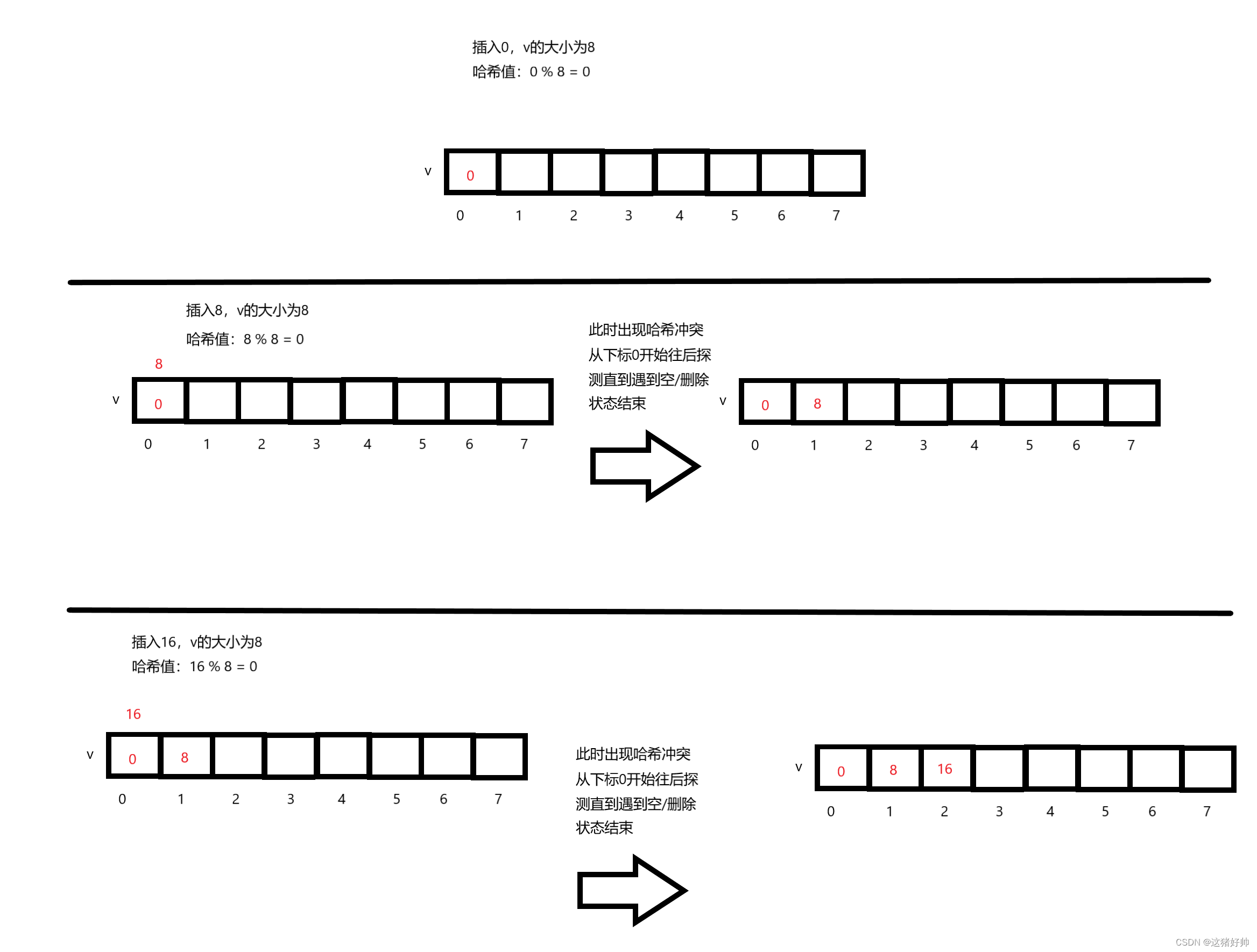
探测法的思想很简单,就是如果哈希值发生冲突,那么就从这个哈希值的后面进行探测
探测下一个位置是否为空/删除状态,如果不是,则继续往后探测,直到遇到为空/删除状态为止
如图数组

我们利用探测法 分别插入0,8,16
结点类
哈希表中数据存储的是一个键值对(pair)
而除了键值对pair以外,用探测法实现的哈希表还需要有一个变量来表示结点此时处于删除/空/存在状态,这个状态我们采用的是用枚举实现
于是结点类的实现如下
enum State
{
EMPTY,//空
DELETE,//删除
EXIST//存在
};
template <class K, class V>
struct HashData
{
pair<K, V> _kv;
State _state = EMPTY;
};插入数据(insert)
在插入数据之前我们需要知道的是,哈希表是什么扩容的?存储满再扩容吗?
答案是并不是,原因是当vector的存储数据个数已经快满了以后,哈希表再进行探测插入的话探测的次数就会变多,而此时效率也会变低,所以我们需要在哈希表快满的时候就进行扩容,那么什么时候算快满了呢?
冲突因子
冲突因子 = 哈希表中有的数据 / 哈希表的大小
而我们通过控制冲突因子来控制扩容,当冲突因子的大小>某个值时,我们就进行扩容
这里的某个值跟vector的扩容一样,是由用户自定义的
一般我们设置为0.7即可
数据扩容
哈希表的扩容不能跟vector一样直接拷贝数据到新表
因为哈希表需要根据数据的哈希值映射到不同的地方存储
哈希值会根据表大小的不同算出不同的哈希值
例如:
96在原大小为10的的表中哈希值为6,但如果表大小扩到20,那么此时96映射的位置为16
既然如此如何处理呢?那么我们就需要先创建一个新表,然后把数据一个一个的重新映射到新表当中
哈希值
此时还面临一个问题,我们以上举例都为整形家族的,可以直接求出哈希值,但如果这个类型不是整形家族的呢?例如:string、日期类。。。
那么此时我们需要一个仿函数来求出这个类型的哈希值
需要注意的是:这个类型通过仿函数求出的哈希值必须是整形家族的,而这个哈希值我们也必须在插入以后能再次找到
插入的代码实现以及哈希类
//hash为仿函数模板
template <class K, class V, class hash>
class HashTable
{
typedef HashData<K, V> Data;
private:
vector<Data> _table;//哈希表
size_t _count = 0;//有效数据的个数
public:
bool insert(const pair<K, V> &val)
{
//1、判断数据是否存在
if (Find(val.first))
{
return false;
}
//2、判断是否扩容
//因为_count / _table.size() = 浮点数,所以要把_count * 10 ,这里的冲突因子>=0.7就扩容
if (_table.size() == 0 || _count * 10 / _table.size() >= 7)
{
HashTable<K, V, hash> newtable;
size_t newsize = _table.size() == 0 ? 10 : _table.size() * 2;
newtable._table.resize(newsize);
for (int i = 0; i < _table.size(); ++i)
{
newtable.insert(_table[i]._kv);
}
newtable._table.swap(_table);
}
//3、求出哈希值
hash hs;
size_t hashi = hs(val.first);
hashi %= _table.size();
//4、找到插入的位置
while (_table[hashi]._state == EXIST)
{
hashi++;
hashi %= _table.size();
}
_table[hashi]._kv = val;
_table[hashi]._state = EXIST;
_count++;
return true;
}
};查找数据(find)
查找数据我们就把要查找的值的哈希值求出来,再直接通过哈希值映射到对应的下标后用探测法找数据即可
Data *Find(const K key)
{
if (!_table.size())
{
return nullptr;
}
//求出哈希值并映射下标
hash hs;
size_t hashi = hs(key);
hashi %= _table.size();
//探测法找数据
while (_table[hashi]._state == EXIST)
{
if (_table[hashi]._kv.first == key)
{
return &_table[hashi];
}
else
{
hashi++;
hashi %= _table.size();
}
}
return nullptr;
}删除数据(erase)
删除数据我们需要先找到这个数据,再把这个数据的状态设置为DELETE即可
bool erase(const K& key)
{
Data* pNode = Find(key);
if(pNode == nullptr)
{
//没找到
return false;
}
else
{
//找到了
pNode->_state = DELETE;
return true;
}
}第二种方法:拉链法实现哈希表
第二种方法也是为了解决哈希冲突而实现的
我们知道探测法的解决办法是发生冲突的位置往后探测,直到遇到空/删除的位置插入即可
而拉链法是把发生冲突的数据用一个链表串联起来
如图
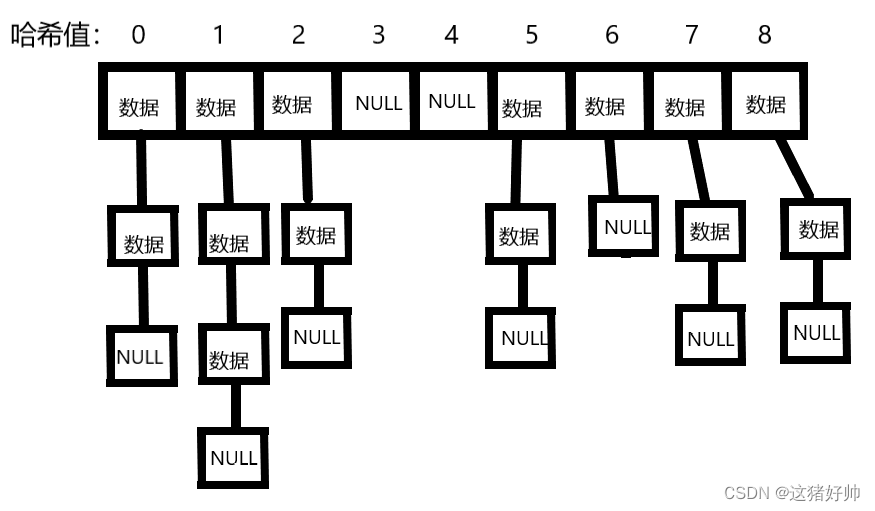
由上图可知,用拉链法实现的哈希表是由一个个链表组成的,所以此方法下的哈希表我们可以使用指针数组实现,并且这个链表我们用单链表实现即可
结点类
此方法下的结点类不需要再有状态因子了,只需要有数据+指针即可
template<class K,class V>
struct HashData
{
std::pair<K,V> _kv;
HashData<K,V>* _next;
HashData(const std::pair<K,V> kv)
:_kv(kv)
,_next(nullptr)
{
}
};哈希类的成员
成员是由一个存储链表的数组实现的,并且还需要有一个值来存储有效数据的个数
template<class K,class V,class Hash = HashFunc<K>>
class HashTable
{
typedef HashData<K,V> Data;
private:
std::vector<Data*> _table;//表
size_t _count = 0;//表内有效数据
public:
//...
}插入(insert)
插入需要分为两步:
第一步:考虑扩容
第二步:插入数据
扩容
扩容同样需要创建新表,但不需要把原表中的结点释放掉,因为原表中的每一个结点都是我们申请的,如果我们直接释放掉原表中的结点再重新开辟,显然就会导致效率变低
我们只需要把原表的结点重新映射到新表中即可
如下图
我们只需把表中的数据全部放到新表中,再把旧表里的结点全部置为空即可
插入数据
插入数据分为步:
第一步:求出哈希值
第二步:哈希值映射下标
第三步:单链表的插入
插入代码总结:
bool insert(const std::pair<K,V> val)
{
//扩容
if(find(val.first))
{
return false;
}
Hash hs;
if(_count == _table.size())//冲突因子 = 1
{
size_t newCapacity = _table.size() == 0 ? 10 : 2 * _table.size();
HashTable<K,V,Hash> newTable;
newTable._table.resize(newCapacity);
//拷贝一张表的数据
for(size_t i = 0 ; i < _table.size() ; ++i)
{
Data* cur = _table[i];
//拷贝一串链表的数据
while(cur)
{
size_t hashi = hs(cur->_kv.first) % newTable._table.size();
if(newTable._table[hashi])
{
cur->_next = newTable._table[hashi]->_next;
newTable._table[hashi]->_next = cur;
}
else
{
newTable._table[hashi] = cur;
}
cur = cur->_next;
}
_table[i] = nullptr;
}
*this = newTable;
}
//插入数据
Data* node = new Data(val);
size_t hashi = hs(node->_kv.first);
hashi %= _table.size();
if(_table[hashi])
{
node->_next = _table[hashi]->_next;
_table[hashi]->_next = node;
}
else
{
_table[hashi] = node;
}
_count++;
return true;
}
};查找(find)
Data* find(const K& key)
{
Hash hs;
size_t hashi = hs(key);
hashi %= _table.size();
Data* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}删除数据(erase)
删除数据也并不复杂,首先我们需要找到数据,再用删除单链表结点的方式进行删除即可
我们需要求出哈希值找到对应结点所在的链表,再用cur逐个遍历这个链表,并且还需要一个prev结点来记录cur的前一个结点,方便单链表的中间删除
当找到数据后要分为两种情况:
第一种情况:结点是所在链表的头节点
如图

第二种情况:结点不是所在链表的头节点
如图

删除代码总结:
bool erase(const K& key)
{
Hash hs;
size_t hashi = hs(key);
hashi %= _table.size();
Data* cur = _table[hashi];
Data* prev = _table[hashi];//这个结点是用来记录cur的前一个结点,方便单链表不是头的删除
while (cur)
{
if (cur->_kv.first == key)
{
//第一种情况,删除链表的头节点
if (cur == _table[hashi])
{
Data* next = cur->_next;
_table[hashi] = next;
delete cur;
return true;
}
//第二种情况:删除不是头的结点
else
{
prev->_next = cur->_next;
delete cur;
return true;
}
}
prev = cur;
cur = cur->_next;
}
//没找到
return false;
}
};那么我们这期HashTable内容就到这了,感谢大家的支持