TreeMap数据结构及源码解析
- 1.TreeMap的特点
- 2.TreeMap的数据结构
- 2.1二叉查找树
- 2.1.1二叉查找树的定义
- 2.1.2二叉查找树的查找操作
- 2.2平衡二叉树
- 2.2.1平衡二叉树的定义
- 2.2.2平衡二叉树的旋转
- 2.3红黑树
- 2.3.1红黑树的定义
- 2.TreeMap的源码分析
- 2.1get()获取方法分析
- 2.2put()添加方法分析
- 3.自定义TreeMap集合
面试TP-LINK后感觉自己对TreeMap掌握存在疏漏,这里跟学一下TreeMap的知识,原视频如下:
java教程进阶-TreeMap数据结构及源码解析
1.TreeMap的特点
-
概念:
TreeMap是一个双列集合,是Map的子类。底层由红黑树结构构成。
-
特点:
- 元素中键不能重复
- 元素会按照大小顺序排序
例证如下:
元素不能重复,重复会覆盖
public class Demo {
@Test
public void test() {
// 创建对象
TreeMap<Integer, String> map = new TreeMap<>();
// 添加元素
map.put(1, "abc");
map.put(1, "def");
map.put(1, "ghi");
System.out.println(map);
}
}
输出结果:
{1=ghi}
key的取出顺序和放入顺序无关,会按照key从小到大默认排序
@Test
public void test() {
// 创建对象
TreeMap<Integer, String> map = new TreeMap<>();
// 添加元素
map.put(9, "abc");
map.put(2, "def");
map.put(1, "ghi");
System.out.println(map);
}
输出结果:
{1=ghi, 2=def, 9=abc}
2.TreeMap的数据结构
TreeMap底层由红黑树构成,而红黑树是一种特殊的二叉查找树。
常见的树型结构:

2.1二叉查找树
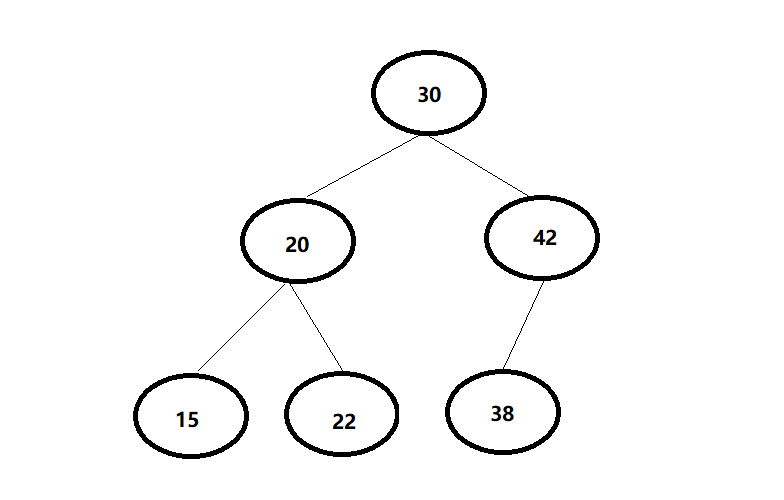
符合以下特点的树,称为二叉查找树
2.1.1二叉查找树的定义
- 特点:
1.若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2.若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3.左、右子树也分别为二叉排序树;
4.没有相等的结点;
-
结论:
二叉查找树就是每个结点的值按照大小排列的二叉树,二叉查找树方便对结点的值进行查找。
-
图:
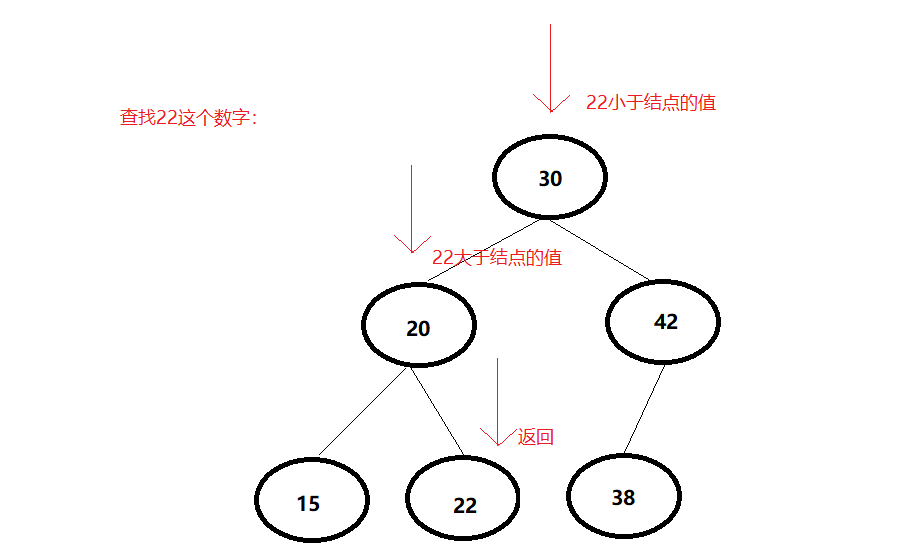
2.1.2二叉查找树的查找操作
- 查找方式:
从根结点开始,如果要查找的数据等于结点的值, 那就返回。
如果要查找的数据小于结点的值,那就在左子树中递归查找;
如果要查找的数据大于结点的值,那就在右子树中递归查找。
- 图:
2.2平衡二叉树
2.2.1平衡二叉树的定义
为了避免出现"瘸子"的现象,减少树的高度,提高我们的搜素效率,又存在一种树的结构:“平衡二叉树”
它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
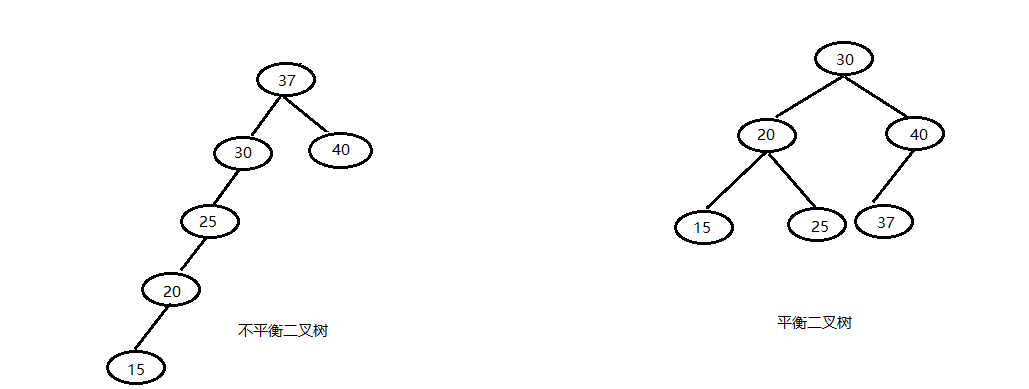
2.2.2平衡二叉树的旋转
- 概念:
在构建一棵平衡二叉树的过程中,当有新的结点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构。
-
两种旋转方式:
-
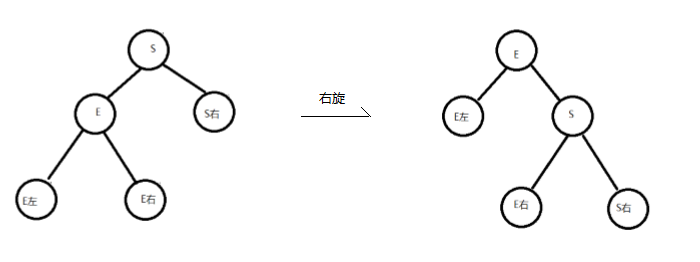
左旋:
左旋就是将结点的右支往左拉,右子结点变成父结点,并把晋升之后多余的左子结点出让给降级结点的 右子结点;
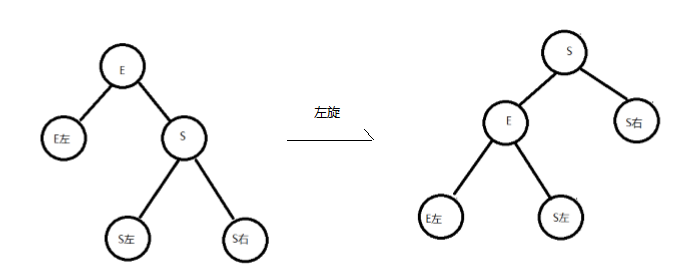
-
右旋:
将结点的左支往右拉,左子结点变成了父结点,并把晋升之后多余的右子结点出让给降级结点的 左子结点
-
-
四种失衡情况:
-
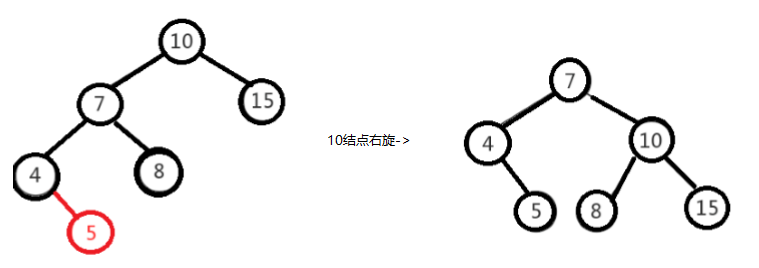
左左情况,需要以10为基准结点进行右旋
-
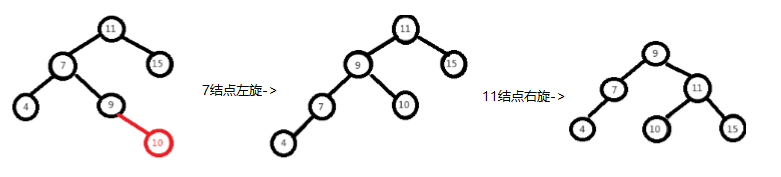
左右情况,先以7为基准结点进行左旋,再以11为基准结点进行右旋
-
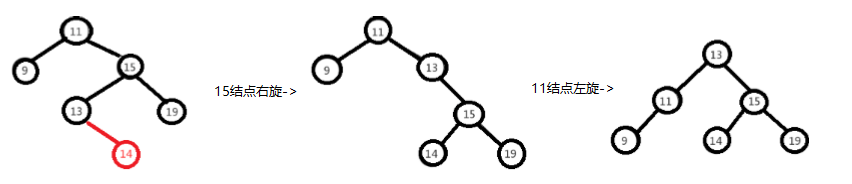
右左情况,先以15为基准结点进行右旋,再以11为基准结点进行左旋
-
右右情况,以11未基准结点进行左旋
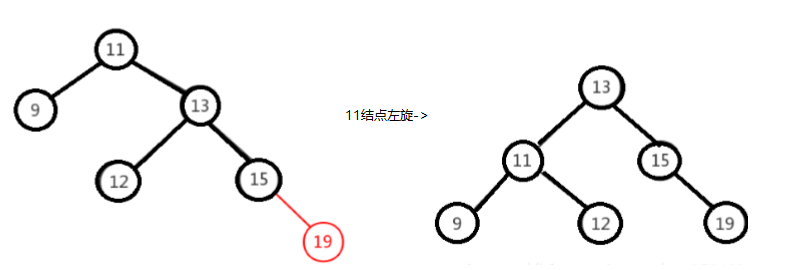
-
2.3红黑树
2.3.1红黑树的定义
-
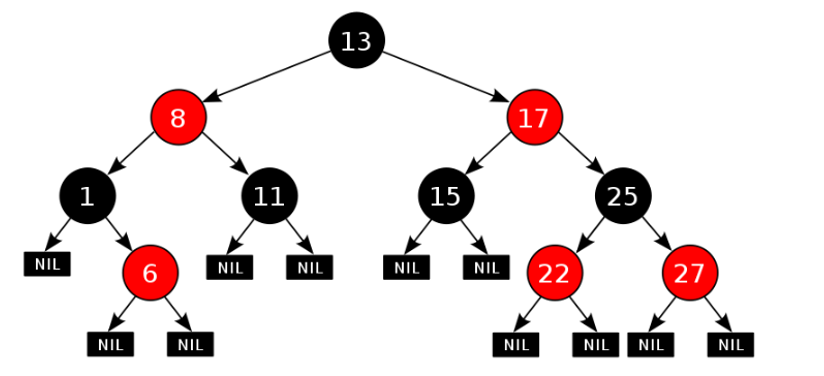
概述:
红黑树是一种自平衡的二叉查找树。
红黑树的每一个结点上都有存储位表示结点的颜色,可以是红或者黑。
红黑树不是高度平衡的,它的平衡是通过"红黑树的特性"进行实现的。
-
红黑树的特性:
- 每一个结点或是红色的,或者是黑色的;
- 根结点必须是黑色;
- 每个叶结点是黑色的(叶结点是Nil)
- 如果某一个结点是红色,那么它的子结点必须是黑色(不能出现两个红色结点相连的情况)
- 对每一个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点;
- 红黑树中左右子树的深度差不能超过短的二倍(例如左子树深度2,右子树深度4,这种就是不符合的)
-
图:
2.TreeMap的源码分析
2.1get()获取方法分析
@Test
public void test() {
// 创建对象
TreeMap<Integer, String> map = new TreeMap<>();
// 添加元素
map.put(9, "abc");
map.put(2, "def");
map.put(1, "ghi");
String s = map.get(2);
System.out.println(s);
}
输出结果:
def
我们看一下get()方法的源码
public V get(Object key) {
//调用方法根据键获取Entry对象
Entry<K,V> p = getEntry(key);
//判断对象如果是null返回null,如果不是null返回对象中的值
return (p==null ? null : p.value);
}
其中Entry<K,V>是什么呢,不妨继续看一下源码
//Entry类型表示结点
static final class Entry<K,V> implements Map.Entry<K,V> {
K key; //key表示键
V value; //value表示值
Entry<K,V> left; //left表示左子结点的地址
Entry<K,V> right; //rigth表示右子结点的地址
Entry<K,V> parent; //parent表示父结点的地址
boolean color = BLACK; //color表示结点的颜色
//下面方法省略…………
}
具体getEntry()方法如下:可以看出来
TreeMap中key不允许为null
final Entry<K,V> getEntry(Object key) {
//判断有没有传入comparator
if (comparator != null)
//调用方法,使用比较器做查询
return getEntryUsingComparator(key);
//判断传入的键是否为null
if (key == null)
//如果要查询的键是null则抛出空指针异常
throw new NullPointerException();
@SuppressWarnings("unchecked")
//把Object类型的键向下转型为Comparable
Comparable<? super K> k = (Comparable<? super K>) key;
//先把二叉树的根结点赋值给p
Entry<K,V> p = root;
//如果p不为null,一直循环比较
while (p != null) {
//调用Comparable的compareTo()方法进行比较
int cmp = k.compareTo(p.key);
//如果cmp小于0,表示要查找的键小于结点的数字
if (cmp < 0)
//把p左子结点赋值给p对象
p = p.left;
//如果cmp大于0,表示要查找的键大于结点的数字
else if (cmp > 0)
//把P右子结点赋值给p对象
p = p.right;
else
//要查找的键等于结点的值,就把当前Entry对象直接返回
return p;
}
//已经找到叶子结点,没有找到要查找的数字返回null
return null;
}
传入比较器之后,通过比较器查询
//传入比较器的情况下
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
//把Object类型的Key向下转型为对应的键的类型
K k = (K) key;
//给比较器对象起名字cpr
Comparator<? super K> cpr = comparator;
if (cpr != null) {
//把二叉树的根结点赋值给P对象
Entry<K,V> p = root;
//循环用要查找的数字和结点中的数字进行比较
while (p != null) {
//调用比较器的compare()
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}
2.2put()添加方法分析
public V put(K key, V value) {
//获取根结点赋值给变量t
Entry<K,V> t = root;
//判断根结点是否为null
if (t == null) {
//对key进行非空和类型校验
compare(key, key);
//新建一个结点
root = new Entry<>(key, value, null);
//设置集合长度为1
size = 1;
//记录集合被修改的次数
modCount++;
//添加成功返回null
return null;
}
这里看一下compare方法具体是啥
如果put的key是null的情况下会抛出空指针异常,或者说key即没有实现comparator比较器,也没有实现Comparable接口的话,也会抛出空指针异常。
// 非空和类型校验
final int compare(Object k1, Object k2) {
return comparator==null ? ((Comparable<? super K>)k1).compareTo((K)k2)
: comparator.compare((K)k1, (K)k2);
}
接着看put()方法的下半部分
//如果根结点不是null则执行下面代码
int cmp;
Entry<K,V> parent;
//把比较器对象赋值给变量cpr
Comparator<? super K> cpr = comparator;
//判断比较器对象如果不是空则执行下面代码
if (cpr != null) {
do {
//把当前结点赋值给变量parent
parent = t;
//比较当前结点的键和要存储的键的大小
cmp = cpr.compare(key, t.key);
//如果要存储的键小于当前结点,则继续和左边的结点进行比较
if (cmp < 0)
t = t.left;
//如果要存储的键大于当前结点,则继续和右边的结点进行比较
else if (cmp > 0)
t = t.right;
else
//如果要存储的键等于当前结点的键,则调用setValue()方法设置新的值
//并结束循环
return t.setValue(value);
//循环直到遍历到叶子结点结束为止
} while (t != null);
}
//如果比较器对象是空则执行下面代码
else {
//如果要保存的键为空,抛出空指针异常
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
//把键转型为Comparable类型
Comparable<? super K> k = (Comparable<? super K>) key;
do {
//把当前结点赋值给变量parent
parent = t;
//比较要存储的键和当前结点的键
cmp = k.compareTo(t.key);
//如果要存储的键小于当前结点,则继续和左边的结点比较
if (cmp < 0)
t = t.left;
//如果要存储的键大于当前结点,则继续和右边的结点比较
else if (cmp > 0)
t = t.right;
else
//如果要存储的键等于当前结点的键,则调用setValue()方法设置新的值
//并结束循环
return t.setValue(value);
//循环直到遍历到叶子结点结束为止
} while (t != null);
}
//遍历结束如果没有找到相同的键,则执行下面代码
//创建新的结点对象,保存键值对,设置父结点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新的键小于父结点的键,则保存在左边
if (cmp < 0)
parent.left = e;
else
//如果新的键大于父结点的键,则保存在右边
parent.right = e;
//维持红黑树的平衡
fixAfterInsertion(e);
//集合长度加一
size++;
//集合修改次数加一
modCount++;
//返回被覆盖的值是null
return null;
}
3.自定义TreeMap集合
使用二叉树实现TreeMap集合,编写put(),get(),remove()等关键方法。
package com.exercise;
import java.util.Comparator;
/**
* 自定义一个TreeMap
*
* @author wty
* @date 2023/6/23 11:31
*/
public class MyTreeMap<K, V> {
// 自定义一个内部类
private class Entry<K, V> {
// 键
K key;
// 值
V value;
// 左子结点
Entry<K, V> left;
// 右子结点
Entry<K, V> right;
// 父结点
Entry<K, V> parent;
//有参构造器
public Entry(K key, V value, Entry<K, V> left, Entry<K, V> right, Entry<K, V> parent) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
this.parent = parent;
}
}
// 定义一个比较器
private final Comparator<? super K> comparator;
// 无参构造给comparator赋值
public MyTreeMap() {
comparator = null;
}
// 有参构造给comparator赋值
public MyTreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}
// 根结点
private Entry<K, V> root;
// 定义集合的长度
private int size;
/**
* @param
* @return int
* @description //获取长度
* @date 2023/6/23 19:09
* @author wty
**/
public int size() {
return size;
}
/**
* @param
* @return V
* @description //根据键获取值
* @param: k
* @date 2023/6/23 19:10
* @author wty
**/
public V get(K key) {
Entry<K, V> entry = getEntry(key);
return null == entry ? null : entry.value;
}
/**
* @param
* @return com.exercise.MyTreeMap<K, V>.Entry<K,V>
* @description //根据键获取值(通用方法)
* @param: key
* @date 2023/6/23 19:11
* @author wty
**/
private Entry<K, V> getEntry(Object key) {
// 非空校验
if (null == key) {
throw new NullPointerException();
}
// 给跟结点起一个名字
Entry<K, V> t = root;
// 判断有没有传入比较器
// 传入了比较器
if (null != comparator) {
// 向下转型
K k = (K) key;
// 循环
while (null != t) {
int cmp = comparator.compare(k, t.key);
if (cmp < 0) {
t = t.left;
} else if (cmp > 0) {
t = t.right;
} else {
return t;
}
}
} else {
// 没有传入比较器
Comparable<K> k = (Comparable<K>) key;
while (null != t) {
int cmp = k.compareTo(t.key);
if (cmp > 0) {
t = t.right;
} else if (cmp < 0) {
t = t.left;
} else {
return t;
}
}
}
// 如果找不到,就返回null
return null;
}
/**
* @param
* @return java.lang.String
* @description //添加元素
* @param: key
* @param: value
* @date 2023/6/23 19:19
* @author wty
**/
public V put(K key, V value) {
//给根结点赋值
Entry<K, V> t = root;
// 非空校验
if (null == key) {
throw new NullPointerException();
}
// 判断集合是否为空
if (null == t) {
// 创建一个新的结点
Entry<K, V> entry = new Entry<>(key, value, null, null, null);
// 给根结点赋值
root = entry;
// 集合长度+1
size++;
return null;
}
// 创建键值对,表示新增结点的父结点
Entry<K, V> parent = t;
int cmp = 0;
// 判断是否有比较器
// 有比较器
if (null != comparator) {
while (null != t) {
parent = t;
//判断键
cmp = comparator.compare(key, t.key);
if (cmp > 0) {
t = t.right;
} else if (cmp < 0) {
t = t.left;
} else {
// 用新的值替换旧的值,把旧的值替换掉
V v = t.value;
t.value = value;
return v;
}
}
} else {
// 没有比较器
Comparable<? super K> k = (Comparable<? super K>) key;
while (null != t) {
parent = t;
cmp = k.compareTo(t.key);
if (cmp > 0) {
t = t.right;
} else if (cmp < 0) {
t = t.left;
} else {
// 用新的值替换旧的值,把旧的值替换掉
V v = t.value;
t.value = value;
return v;
}
}
}
// 要添加的键值对 键不重复
Entry<K, V> entry = new Entry<>(key, value, null, null, parent);
if (cmp > 0) {
parent.right = entry;
} else {
parent.left = entry;
}
// 集合长度增加
size++;
return null;
}
/**
* @param
* @return V
* @description //移除元素
* @param: key
* @date 2023/6/23 19:30
* @author wty
**/
public V remove(K key) {
Entry<K, V> entry = getEntry(key);
if (null == entry) {
return null;
}
// 删除操作
// 1.删除中间结点
// 1.1没有左子树,只有右子树
if (entry.left == null && entry.right != null) {
// 判断要删除的结点是父结点的右子结点
if (entry.parent.right == entry) {
entry.parent.right = entry.right;
} else if (entry.parent.left == entry) {
entry.parent.left = entry.right;
} else {
root = entry.right;
}
// 让被删除结点的子结点,指向父结点
entry.right.parent = entry.parent;
}
// 1.2没有右子树,只有左子树
else if (entry.right == null && entry.left != null) {
// 判断要删除的结点是父结点的右子结点
if (entry.parent.right == entry) {
entry.parent.right = entry.left;
} else if (entry.parent.left == entry) {
entry.parent.left = entry.left;
} else {
root = entry.left;
}
// 让被删除结点的子结点,指向父结点
entry.left.parent = entry.parent;
}
// 2.删除根结点 既有右子树,又有左子树
else if (entry.right != null && entry.left != null) {
//找到后继结点
Entry<K, V> target = entry.right;
// 用右子树的最左子结点去替换
while (target.left != null) {
target = target.left;
}
// 右子结点作为后继结点
if (entry.right == target) {
target.parent = entry.parent;
if (entry == root) {
root = target;
} else if (entry.parent.right == entry) {
entry.parent.right = target;
} else if (entry.parent.left == entry) {
entry.parent.left = target;
}
// 被删除结点左子结点重新指向新的父结点
entry.left.parent = target;
target.left = entry.left;
} else {
// 右子树的最左子结点作为后继结点
if (target.right == null) {
// 后继结点没有子结点
target.parent.left = null;
} else {
// 后继结点有子结点
target.parent.left = target.right;
target.right = target.parent;
}
// 让后继结点替换掉被删除结点
if (entry == root) {
root = target;
} else if (entry.parent.right == entry) {
entry.parent.right = target;
} else if (entry.parent.left == entry) {
entry.parent.left = target;
}
// 被删除结点左右子树需要指向后继结点
entry.left.parent = target;
entry.right.parent = target;
target.left = entry.left;
target.right = entry.right;
}
} else {
// 3.删除叶子结点
if (entry.parent.right == entry) {
entry.parent.right = null;
} else if (entry.parent.left == entry) {
entry.parent.left = null;
} else {
root = null;
}
}
// 给集合长度减少1
size--;
return entry.value;
}
/**
* @param
* @return java.lang.String
* @description //打印树的结构
* @date 2023/6/23 19:55
* @author wty
**/
@Override
public String toString() {
// 非空检验
if (null == root) {
return "{}";
}
String s = "{";
String s1 = methodToString(root);
s = s + s1.substring(0, s1.length() - 2) + "}";
return s;
}
/**
* @param
* @return java.lang.String
* @description //打印树的结构(递归调用)
* @param: entry
* @date 2023/6/23 19:55
* @author wty
**/
private String methodToString(Entry<K, V> entry) {
String s = "";
// 拼接左子树
if (entry.left != null) {
s += methodToString(entry.left);
}
// 拼接中间结点
s += entry.key + "=" + entry.value + ", ";
// 拼接右子树
if (entry.right != null) {
s += methodToString(entry.right);
}
return s;
}
}
- 测试类
@Test
public void test() {
MyTreeMap<Integer, String> treeMap = new MyTreeMap<>();
treeMap.put(5, "abc");
treeMap.put(3, "def");
treeMap.put(6, "ghi");
treeMap.put(1, "jkl");
treeMap.put(4, "mno");
System.out.println(treeMap);
}
运行结果:
{1=jkl, 3=def, 4=mno, 5=abc, 6=ghi}
继续测试get
@Test
public void test() {
MyTreeMap<Integer, String> treeMap = new MyTreeMap<>();
treeMap.put(5, "abc");
treeMap.put(3, "def");
treeMap.put(6, "ghi");
treeMap.put(1, "jkl");
treeMap.put(4, "mno");
System.out.println(treeMap);
System.out.println(treeMap.get(3));
}
运行结果:
{1=jkl, 3=def, 4=mno, 5=abc, 6=ghi}
def
最后测试一下删除remove方法
@Test
public void test() {
MyTreeMap<Integer, String> treeMap = new MyTreeMap<>();
treeMap.put(5, "abc");
treeMap.put(3, "def");
treeMap.put(6, "ghi");
treeMap.put(1, "jkl");
treeMap.put(4, "mno");
System.out.println(treeMap);
System.out.println(treeMap.get(3));
treeMap.remove(4);
System.out.println(treeMap);
}
运行结果:
{1=jkl, 3=def, 4=mno, 5=abc, 6=ghi}
def
{1=jkl, 3=def, 5=abc, 6=ghi}





![[易语言][部署]使用易语言部署paddleocr的onnx模型api接口推理直接调用](https://i1.hdslb.com/bfs/archive/e37a5562f478e7b699888069f72b2191694ede8e.jpg@100w_100h_1c.png@57w_57h_1c.png)