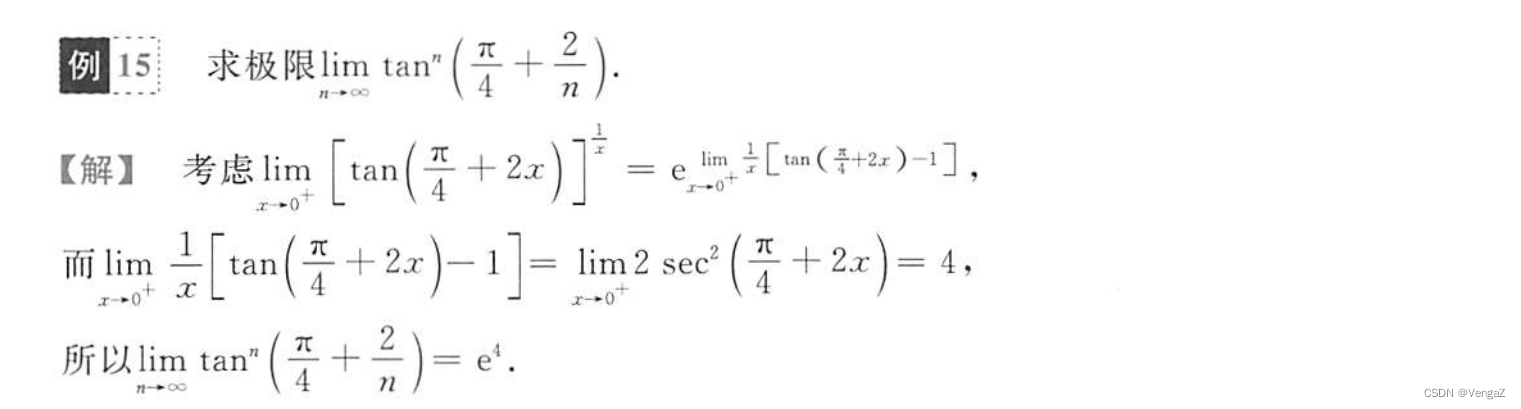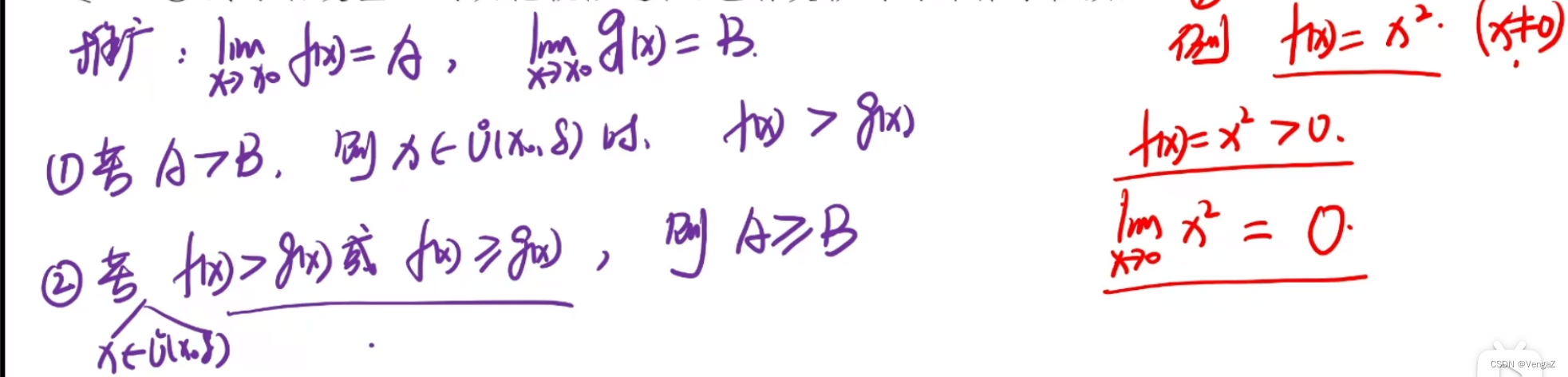目录
- 第一章 函数 极限 连续
- 第一节 函数
- 第二节 极限
- 一、极限的概念与性质
- 数列的极限
- 例1
- 例2
- 函数的极限
- 极限的性质(保号性重点 有界性)
- 例12
- 例13
- 例14
- `函数极限与数列极限的关系`
- 例15
第一章 函数 极限 连续
第一节 函数
判断有界要用函数的绝对值,并且这里的不等式解法需要注意

需要注意这里的论证方式

第二节 极限
一、极限的概念与性质
数列的极限

奇数子列要收敛于a,偶数子列也需要收敛于a(以2n为例子,若为3n,则余1、余2、余0的子列都要收敛于a)
拓展出去就是,所有的子列都收敛于a,才能说这个数列收敛于a
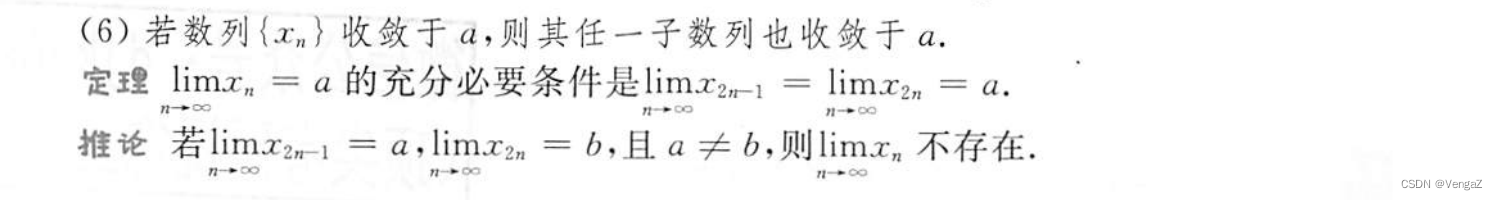
例1
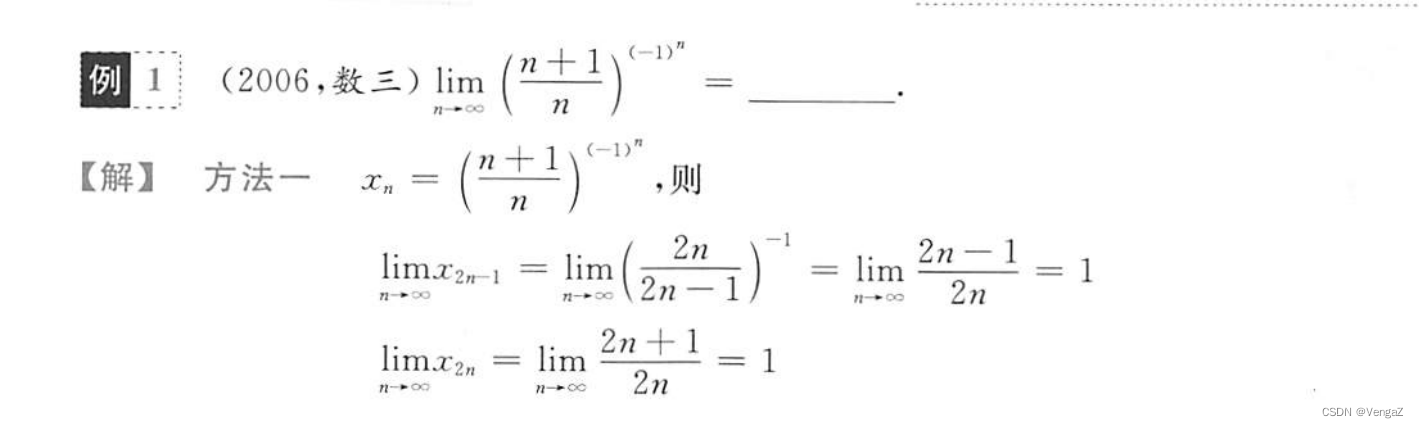
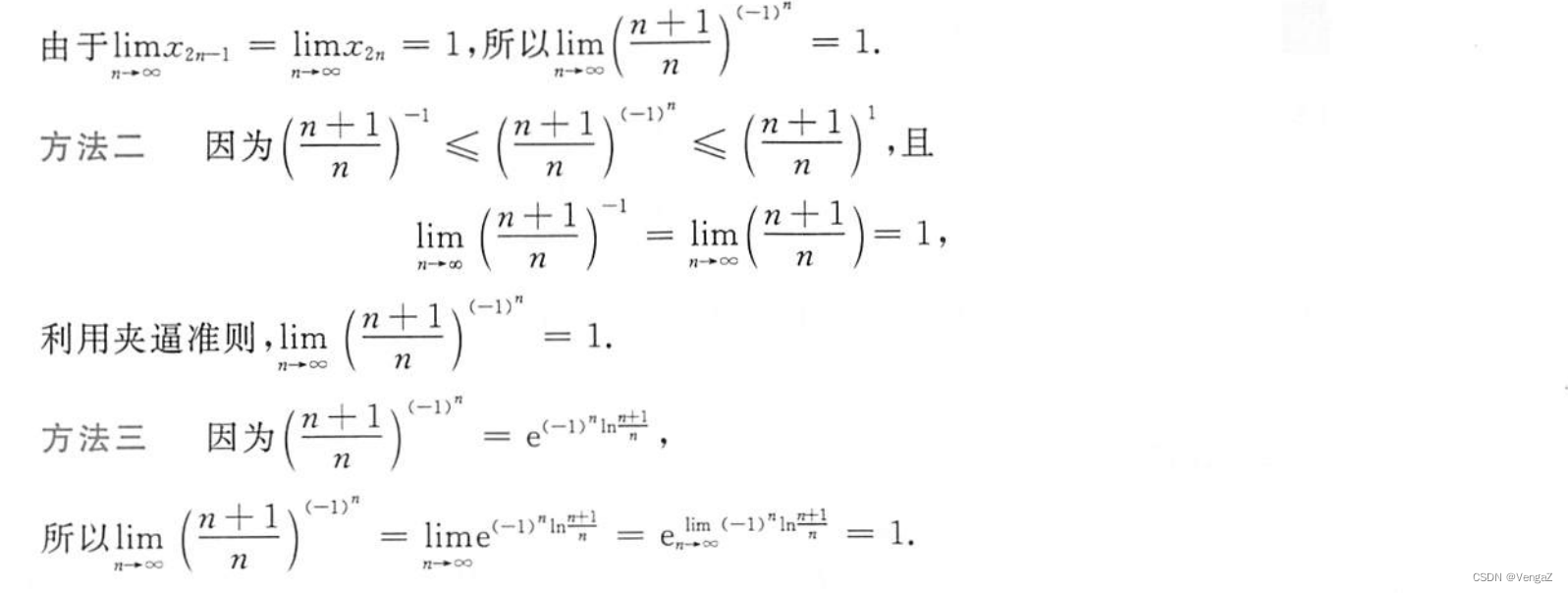
例2

函数的极限
- 自变量趋于无穷大时函数的极限

- 自变量趋于有限值函数的极限

需要注意的有左极限以及右极限
需要分左右极限的状况
极限的性质(保号性重点 有界性)

有界性
数列
数列若收敛则一定有界,反之不成立
有界是有上界或者有下界,上界下界可以相同,这种情况就是收敛
函数
函数极限存在即说明函数在去心邻域有界(局部有界)
反之不成立
局部有界不代表在那个点的函数极限存在
保号性
数列
如果数列趋于无穷时的极限值大于零或者小于零,则存在一个很大的n,使得 x n x_n xn的值大于零或者小于零
如果一个数列存在一个很大的n,使得 x n x_n xn的值大于等于零或者小于等于零,则数列极限也大于等于零或者小于等于零
最主要的原因是,取值可能取不到0,但是极限可以到0
函数
道理同数列
如果极限值大于则去心邻域也大于
如果函数大于或者大于等于,则极限值大于等于
例12

例13

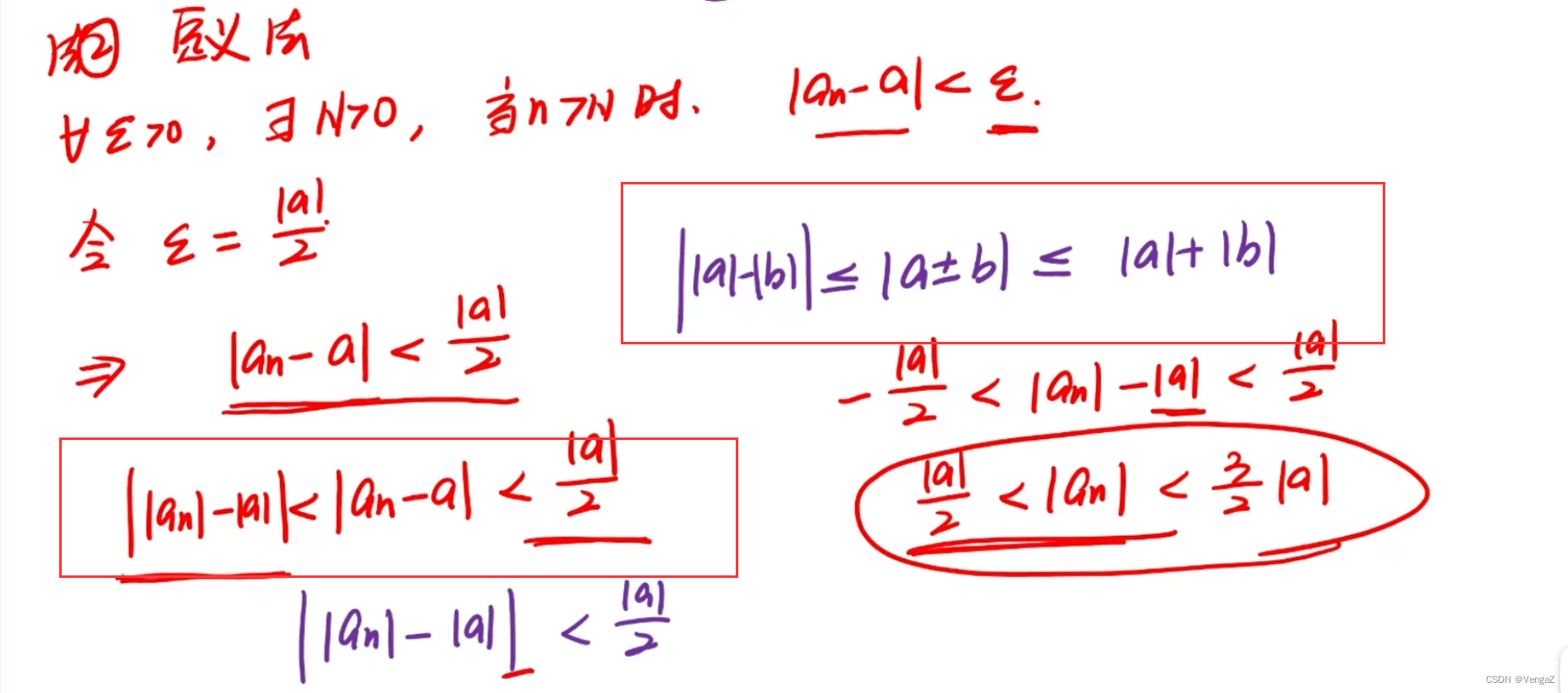
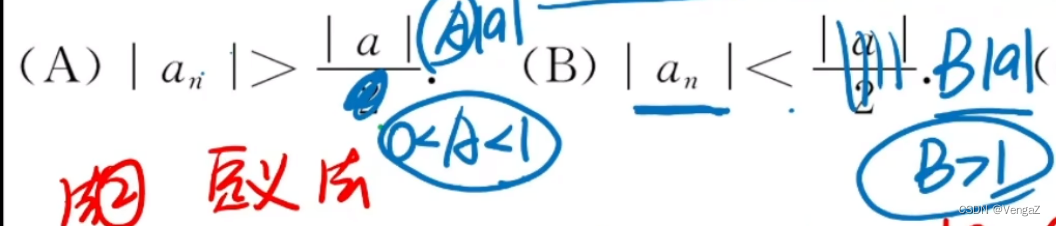
大于什么系数大于零小于一;小于什么系数大于一
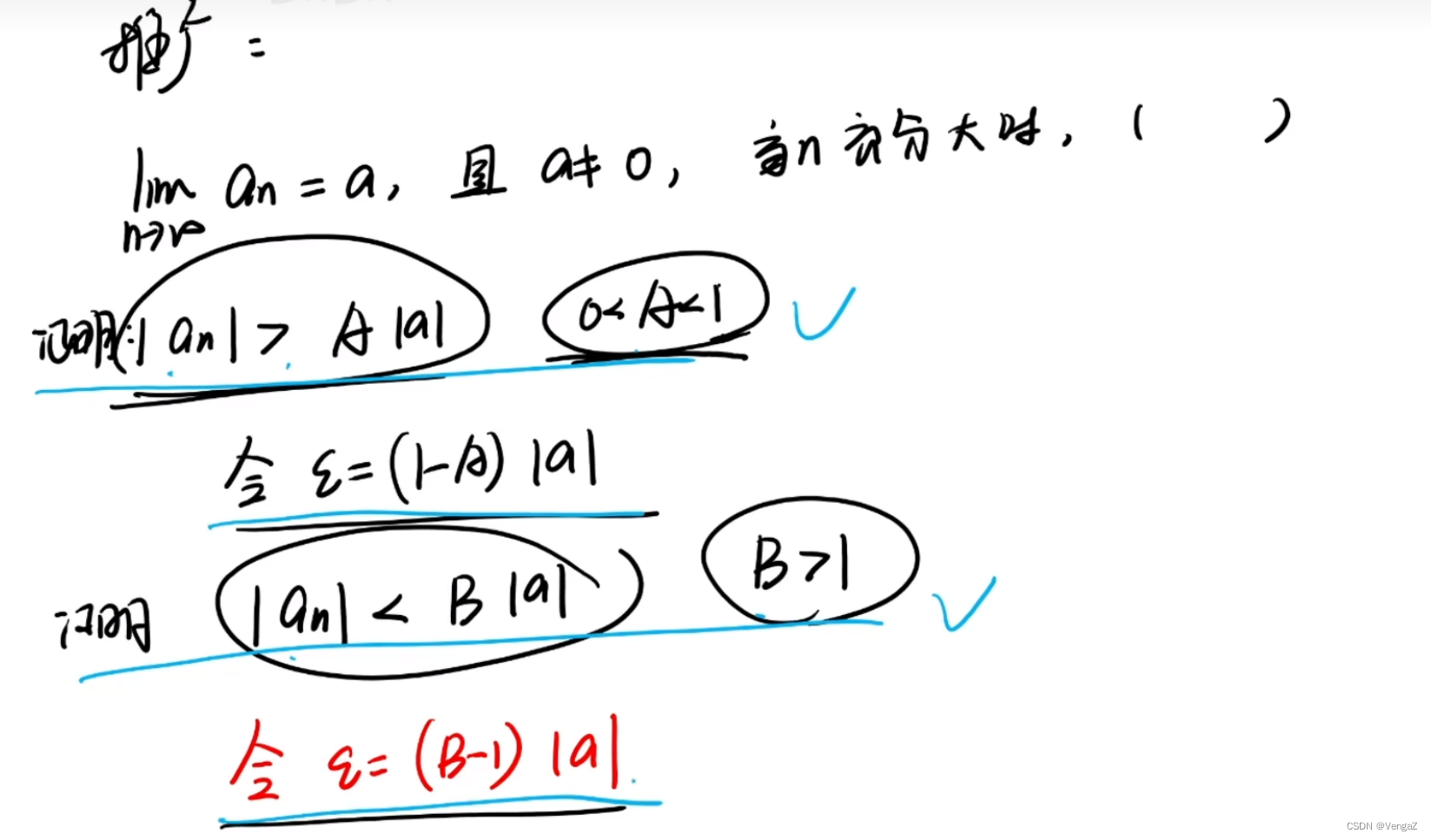
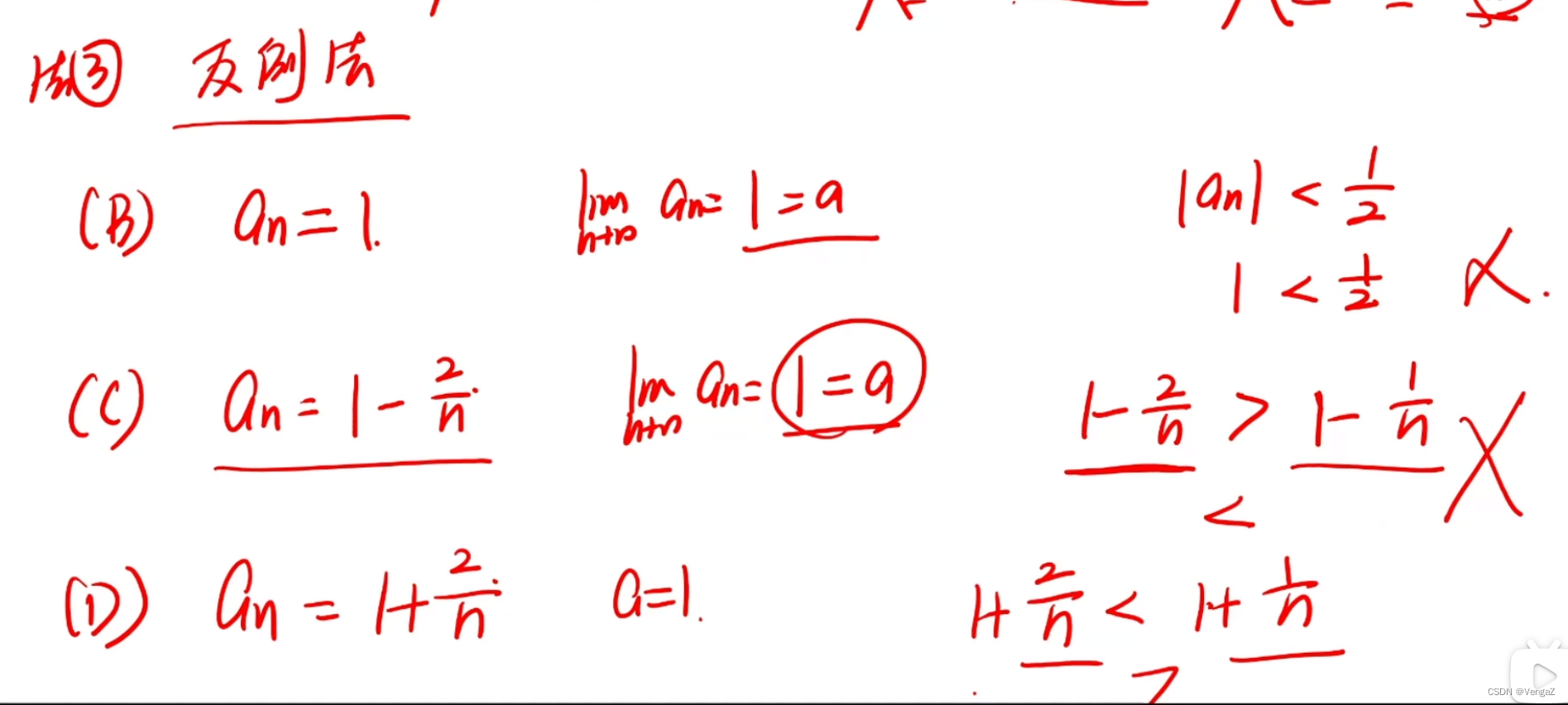
例14
局部有界连续判定

函数极限与数列极限的关系

例15