文章目录
- @[toc]
- 1.状态空间模型
- 1.1.连续状态空间模型
- 1.2.离散状态空间模型
- 2.矩阵微积分
- 3.二次规划
- 4.概率论
- 4.1.期望与方差
- 4.2.独立事件
- 4.3.向量随机变量
- 4.4.噪声与协方差矩阵
- 4.5.条件概率
- 5.最小二乘估计
- 5.1.加权最小二乘估计
- 5.2.递推最小二乘估计
- 5.3.状态向量和协方差随时间变化
- 6.离散卡尔曼滤波器
- 7.测量协方差
- 7.1.平均值与协方差得递推公式
- 7.2.测量四足机器人传感器协方差
- 8.离散卡尔曼滤波调参
- 8.1.协方差
- 8.2.腾空&触地
- ref
文章目录
- @[toc]
- 1.状态空间模型
- 1.1.连续状态空间模型
- 1.2.离散状态空间模型
- 2.矩阵微积分
- 3.二次规划
- 4.概率论
- 4.1.期望与方差
- 4.2.独立事件
- 4.3.向量随机变量
- 4.4.噪声与协方差矩阵
- 4.5.条件概率
- 5.最小二乘估计
- 5.1.加权最小二乘估计
- 5.2.递推最小二乘估计
- 5.3.状态向量和协方差随时间变化
- 6.离散卡尔曼滤波器
- 7.测量协方差
- 7.1.平均值与协方差得递推公式
- 7.2.测量四足机器人传感器协方差
- 8.离散卡尔曼滤波调参
- 8.1.协方差
- 8.2.腾空&触地
- ref
1.状态空间模型
- IMU: 加速度计+陀螺仪, 测六轴数据
1.1.连续状态空间模型
- 一个时间连续的, 定长的线性系统
{
x
˙
(
t
)
=
A
c
x
(
t
)
+
B
c
u
(
t
)
y
(
t
)
=
C
c
x
(
t
)
\left\{\begin{matrix} \dot{\bm x}(t)={\bm A}_c{\bm x}(t)+{\bm B}_c{\bm u}(t) \\ {\bm y}(t)={\bm C}_c{\bm x}(t) \end{matrix}\right.
{x˙(t)=Acx(t)+Bcu(t)y(t)=Ccx(t)
- x ( t ) {\bm x}(t) x(t): 系统的状态向量 \;\; u ( t ) {\bm u}(t) u(t): 控制向量 \;\; y ( t ) {\bm y}(t) y(t): 输出向量
- A c {\bm A}_c Ac: 系统矩阵 \;\; B c {\bm B}_c Bc: 输入矩阵 \;\; C c {\bm C}_c Cc: 输出矩阵
- 意义: 系统下一阶段的变化 x ˙ ( t ) \dot{\bm x}(t) x˙(t)与系统当前状态 x ( t ) {\bm x}(t) x(t), 系统当前输入 u ( t ) {\bm u}(t) u(t)有关; 系统输出量 y ( t ) {\bm y}(t) y(t)和系统状态 x ( t ) {\bm x}(t) x(t)有关
- 需要估计的状态量
x
\bm x
x: 世界系{s}下的机器人运动状态
- 机身位置
p
b
{\bm p}_b
pb, 机身速度
v
b
{\bm v}_b
vb, 四个足端位置
p
0
p
1
p
2
p
3
{\bm p_0}\;{\bm p_1}\;{\bm p_2}\;{\bm p_3}
p0p1p2p3, 均为三维向量, 故
x
\bm x
x是18维向量
- x = [ p b v b p 0 p 1 p 2 p 3 ] x=\begin{bmatrix} {\bm p}_b \\ {\bm v}_b \\ {\bm p_0} \\ {\bm p_1} \\ {\bm p_2} \\ {\bm p_3}\end{bmatrix} x= pbvbp0p1p2p3
- 考虑状态向量的导数
x
˙
\dot{\bm x}
x˙, 设四个足端都与地面稳定接触, 则每个足端速度为零
- x ˙ = [ v b R s b a b + g 0 3 × 1 0 3 × 1 0 3 × 1 0 3 × 1 ] \dot{x}=\begin{bmatrix} {\bm v}_b \\ {\bm R}_{sb}{\bm a}_b+{\bm g} \\ {\bm 0}_{3\times1} \\ {\bm 0}_{3\times1} \\ {\bm 0}_{3\times1} \\ {\bm 0}_{3\times1} \end{bmatrix} x˙= vbRsbab+g03×103×103×103×1
- 机身位置
p
b
{\bm p}_b
pb, 机身速度
v
b
{\bm v}_b
vb, 四个足端位置
p
0
p
1
p
2
p
3
{\bm p_0}\;{\bm p_1}\;{\bm p_2}\;{\bm p_3}
p0p1p2p3, 均为三维向量, 故
x
\bm x
x是18维向量
- 可测量的输出量:
- IMU测得{s}的机身姿态 R s b \bm R_{sb} Rsb , {b}的 a b , ω b \bm a_b\;,\;\bm\omega_b ab,ωb;
- 由各关节编码器&正运动学得{b}下足端相对机身位置 p b f B {\bm p}_{bfB} pbfB 和{s}的 p s f B {\bm p}_{sfB} psfB;
- {s}的足端相对机身速度 v s f B \bm v_{sfB} vsfB;
- 又四个足端全触地,高度为0
- 输出向量
y
\bm y
y, 28维向量
- y = [ p s f B 0 p s f B 1 p s f B 2 p s f B 3 v s f B 0 v s f B 1 v s f B 2 v s f B 3 p s z 0 p s z 1 p s z 2 p s z 3 ] \bm y=\begin{bmatrix} {\bm p}_{sfB0} \\ {\bm p}_{sfB1} \\ {\bm p}_{sfB2} \\ {\bm p}_{sfB3} \\ {\bm v}_{sfB0} \\ {\bm v}_{sfB1} \\ {\bm v}_{sfB2} \\ {\bm v}_{sfB3} \\ p_{sz0} \\ p_{sz1} \\ p_{sz2} \\ p_{sz3} \end{bmatrix} y= psfB0psfB1psfB2psfB3vsfB0vsfB1vsfB2vsfB3psz0psz1psz2psz3
1.2.离散状态空间模型
- 程序必然每隔一段时间采样一次数据, 称离散系统, 要使用与之对应的离散状态空间模型, 以
k
k
k表示第k个时刻
- { x ˙ ( k ) = A x ( k − 1 ) + B u ( k − 1 ) y ( k ) = C x ( k ) \left\{ \begin{matrix} \dot{\bm x}(k)={\bm A}{\bm x}(k-1)+{\bm B}{\bm u}(k-1) \\ {\bm y}(k)={\bm C}{\bm x}(k)\end{matrix}\right. {x˙(k)=Ax(k−1)+Bu(k−1)y(k)=Cx(k)
2.矩阵微积分
- 二次型的偏导数计算
-
∂
x
T
A
x
∂
x
=
x
T
A
T
+
x
T
A
\frac{\partial{\bm x}^{\rm T}\bm A x}{\partial \bm x}=\bm x^{\rm T}\bm A^{\rm T}+\bm x^{\rm T}\bm A
∂x∂xTAx=xTAT+xTA
- 对对称矩阵 A = A T \bm A=\bm A^{\rm T} A=AT 有 ∂ x T A x ∂ x = 2 x T A \frac{\partial{\bm x}^{\rm T}\bm A x}{\partial \bm x}=2\bm x^{\rm T}\bm A ∂x∂xTAx=2xTA
-
∂
x
T
A
x
∂
x
=
x
T
A
T
+
x
T
A
\frac{\partial{\bm x}^{\rm T}\bm A x}{\partial \bm x}=\bm x^{\rm T}\bm A^{\rm T}+\bm x^{\rm T}\bm A
∂x∂xTAx=xTAT+xTA
- 对矩阵与向量乘积的偏导数
- ∂ A x ∂ x = A ∂ x T A ∂ x = A T \begin{matrix} \frac{\partial\bm A\bm x}{\partial \bm x}=\bm A \\ \frac{\partial\bm x^{\rm T}\bm A}{\partial \bm x}=\bm A^{\rm T} \end{matrix} ∂x∂Ax=A∂x∂xTA=AT
- 对矩阵的迹
-
∂
T
r
(
A
B
A
T
)
∂
A
=
A
B
T
+
A
B
\frac{ \partial {\rm Tr}(\bm A\bm B\bm A^{\rm T})}{\partial \bm A}=\bm A\bm B^{\rm T}+\bm A\bm B
∂A∂Tr(ABAT)=ABT+AB
- 对对称矩阵 A = A T \bm A=\bm A^{\rm T} A=AT 有 ∂ T r ( A B A T ) ∂ A = 2 A B \frac{ \partial {\rm Tr}(\bm A\bm B\bm A^{\rm T})}{\partial \bm A}=2\bm A\bm B ∂A∂Tr(ABAT)=2AB
-
∂
T
r
(
A
B
A
T
)
∂
A
=
A
B
T
+
A
B
\frac{ \partial {\rm Tr}(\bm A\bm B\bm A^{\rm T})}{\partial \bm A}=\bm A\bm B^{\rm T}+\bm A\bm B
∂A∂Tr(ABAT)=ABT+AB
3.二次规划
- 二次规划QP(Quadratic Programming)广泛用于最优化问题, 卡尔曼滤波器是最优状态估计的一种
- 对 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c求最值, 令 y ˙ = 2 a x + b = 0 \dot{y}=2ax+b=0 y˙=2ax+b=0
- 定义代价函数J为标量
J
=
x
T
A
x
+
b
x
+
c
J=\bm x^{\rm T}\bm A \bm x+\bm b \bm x + c
J=xTAx+bx+c
- 设 A \bm A A为对称矩阵, 正定矩阵, 偏微分 ∂ J ∂ x = 2 A x + b = 0 \frac{\partial J}{\partial \bm x}=2\bm A\bm x+\bm b=0 ∂x∂J=2Ax+b=0
- 当 J J J取最小值, x = − 1 2 A − 1 b \bm x=-\frac{1}{2}\bm A^{-1}\bm b x=−21A−1b, 即二次规划的理论解
正定矩阵 A \bm A A, 对任意非零向量 v \bm v v, 有 v T A v > 0 \bm v^{\rm T}\bm A\bm v>0 vTAv>0
4.概率论
4.1.期望与方差
- 期望
E
(
x
)
\bm E(x)
E(x) 或
x
‾
\overline{x}
x: 平均值
- E ( x + y ) = E ( x ) + E ( y ) E(x+y)=E(x)+E(y) E(x+y)=E(x)+E(y)
- 方差
σ
x
2
\sigma_x^2
σx2 描述随机变量
x
x
x对期望
x
‾
\overline{x}
x的离散程度大小
- σ x 2 = E [ ( x − x ‾ ) 2 ] \sigma_x^2=E[(x-\overline{x})^2] σx2=E[(x−x)2]
- 表示: x ∼ ( E ( x ) , σ x 2 ) x\sim (E(x),\sigma_x^2) x∼(E(x),σx2)
4.2.独立事件
- 协方差 C x y = E [ ( x − x ‾ ) ( y − y ‾ ) ] C_{xy}=E[(x-\overline{x})(y-\overline{y})] Cxy=E[(x−x)(y−y)]
- 一个事件的发生对另一个事件发生的概率无影响, 则两事件互为独立事件, 其协方差 C x y = 0 C_{xy}=0 Cxy=0
4.3.向量随机变量
- 矩阵的期望即对矩阵每个元素分别求期望
- 随机变量
x
y
\bm x\;\bm y
xy 的协方差矩阵
C
x
y
=
E
[
(
x
−
x
‾
)
(
y
−
y
‾
)
T
]
\bm C_{xy}=E[(\bm x-\overline{\bm x})(\bm y-\overline{\bm y})^{\rm T}]
Cxy=E[(x−x)(y−y)T]
- C x y \bm C_{xy} Cxy为对称阵
- 随机变量
x
\bm x
x 和自己的协方差矩阵
C
x
=
E
[
(
x
−
x
‾
)
(
x
−
x
‾
)
T
]
\bm C_{x}=E[(\bm x-\overline{\bm x})(\bm x-\overline{\bm x})^{\rm T}]
Cx=E[(x−x)(x−x)T]
- C x \bm C_x Cx为对称阵, 对角项分别为随机变量 x \bm x x各项的方差
- 若 x \bm x x的各项相互独立, 则协方差矩阵 C x \bm C_x Cx为对角矩阵, 非对角项为0
4.4.噪声与协方差矩阵
- 白噪声:
t
1
t_1
t1时刻噪声向量
v
(
t
1
)
\bm v(t_1)
v(t1)与
t
2
t_2
t2时刻噪声向量
v
(
t
2
)
\bm v(t_2)
v(t2)之间相互独立, 可对任一时刻噪声单独分析
- 协方差矩阵为对角矩阵, 且每一对角项为 v \bm v v对应元素的方差值
- 单四足机器人噪声每一项通常不是相互独立的
4.5.条件概率
- 若随机变量
x
\bm x
x和随机变量
y
\bm y
y之间不独立, 不同
y
\bm y
y值下随机变量
x
\bm x
x期望
E
(
x
)
E(\bm x)
E(x)不同
- 已知 y = y 1 \bm y=\bm y_1 y=y1条件下的 x \bm x x期望表示为 E { x ∣ y 1 } E\{\bm x|\bm y_1\} E{x∣y1}
5.最小二乘估计
- 测量输入向量
y
\bm y
y必包含噪声向量
v
\bm v
v, 设
x
k
\bm x_k
xk定值
- y k = C x + v k \bm y_k=\bm C\bm x+\bm v_k yk=Cx+vk, v ∼ ( 0 , R ) \bm v\sim(0,\bm R) v∼(0,R), R = E ( v v T ) \bm R=E(\bm v\bm v^{\rm T}) R=E(vvT)对角阵
5.1.加权最小二乘估计
- 测量残差
ϵ
y
=
y
−
C
x
^
\bm \epsilon_y=y-\bm C\hat{\bm x}
ϵy=y−Cx^
- 当各项二次方和取得最小值, 状态向量值就是最有估计值 x ^ \hat{\bm x} x^
- 代价函数 J = ϵ y 1 2 + ϵ y 2 2 + . . . + ϵ y n 2 = ϵ y T ϵ y J=\epsilon_{y1}^2+\epsilon_{y2}^2+...+\epsilon_{yn}^2={\bm \epsilon}_{y}^{\rm T}{\bm \epsilon}_{y} J=ϵy12+ϵy22+...+ϵyn2=ϵyTϵy
- 引入加权, 与方差成反比 J = ϵ y 1 2 σ 1 2 + ϵ y 2 2 σ 1 2 + . . . + ϵ y n 2 σ 1 2 = ϵ y T R T ϵ y = ( y − C x ^ ) T R − 1 ( y − C x ^ ) = y T R − 1 y − y T R − 1 C x ^ − x ^ T C T R − 1 y − x ^ T C T R − 1 C x ^ \begin{matrix} J=\frac{\epsilon_{y1}^2}{\sigma_1^2}+\frac{\epsilon_{y2}^2}{\sigma_1^2}+...+\frac{\epsilon_{yn}^2}{\sigma_1^2}={\bm \epsilon}_{y}^{\rm T}{\bm R^{\rm T}}{\bm \epsilon}_{y} \\ =(\bm y-\bm C\hat{\bm x})^{\rm T}{\bm R}^{-1}(\bm y-\bm C\hat{\bm x}) \\= {\bm y^{\rm T}\bm R^{-1}\bm y} - {\bm y^{\rm T}\bm R^{-1}\bm C\hat{\bm x}} - {\hat{\bm x}^{\rm T}\bm C^{\rm T}\bm R^{-1}\bm y} - {\hat{\bm x}^{\rm T}\bm C^{\rm T}\bm R^{-1}\bm C\hat{\bm x}} \end{matrix} J=σ12ϵy12+σ12ϵy22+...+σ12ϵyn2=ϵyTRTϵy=(y−Cx^)TR−1(y−Cx^)=yTR−1y−yTR−1Cx^−x^TCTR−1y−x^TCTR−1Cx^
- 矩阵 R \bm R\; R是对角阵, R − 1 \bm R^{-1} R−1是对角阵, 每一项为 R \bm R R对应项导数
- 由二次规划方法计算代价函数偏导取0
∂
J
∂
x
^
=
−
2
y
T
R
−
1
C
+
2
x
^
T
C
T
R
−
1
C
=
0
\frac{\partial J}{\partial\hat{\bm x}}=-2{\bm y^{\rm T}\bm R^{-1}\bm C}+{2\hat{\bm x}^{\rm T}\bm C^{\rm T}\bm R^{-1}\bm C}=0
∂x^∂J=−2yTR−1C+2x^TCTR−1C=0
- 得对状态 x \bm x x的最优估计结果 x ^ = ( C T R − 1 C ) − 1 C T R − 1 y \hat{\bm x}=(\bm C^{\rm T}\bm R^{-1}\bm C)^{-1}\bm C^{\rm T}\bm R^{-1}\bm y x^=(CTR−1C)−1CTR−1y
5.2.递推最小二乘估计
- 上面的最优估计结果, 要利用一段时间所有测量值 y \bm y y, 矩阵将变得很大, 占用内存影响速度, 故采用递推最小二乘估计
- 状态
x
\bm x
x的最优估计
x
^
\hat{\bm x}
x^递推公式
{
y
k
=
C
x
+
v
k
x
^
k
=
x
^
k
−
1
+
K
k
(
y
k
−
C
x
^
k
−
1
)
\left\{ \begin{matrix} {\bm y}_k={\bm C\bm x}+{\bm v}_k\\ \hat{\bm x}_k=\hat{\bm x}_{k-1}+{\bm K}_k(\bm y_k-\bm C\hat{\bm x}_{k-1})\end{matrix} \right.
{yk=Cx+vkx^k=x^k−1+Kk(yk−Cx^k−1)
- y k \bm y_k yk: 当前时刻的测量结果, 假设状态向量 x \bm x x是固定常量
- v k \bm v_k vk: 当前时刻的噪声向量
- x ^ k − 1 \hat{\bm x}_{k-1} x^k−1: 上一时刻的最优状态估计, 以 K k ( y k − C x ^ k − 1 ) {\bm K_k}(\bm y_k-\bm C\hat{\bm x}_{k-1}) Kk(yk−Cx^k−1)来修正, 得到当前时刻最优状态估计 x ^ k \hat{\bm x}_k x^k
- K k \bm K_k Kk: 最优的修正系数矩阵, 需要求解出最优
- 求解最优的修正系数矩阵
K
k
\bm K_k
Kk
- k k k 时刻的状态估计误差 ω k = x − x k ^ = ⋯ = ( I − K k C ) ω k − 1 − K k v k {\bm\omega_k={\bm x}-\hat{\bm x_k} = \dots = (\bm I - \bm K_k\bm C){\bm \omega}_{k-1}-{\bm K}_k{\bm v}_k} ωk=x−xk^=⋯=(I−KkC)ωk−1−Kkvk
- 使用二次规划, 令
k
k
k时刻各个状态估计误差方差之和最小
- 代价函数
J
k
=
E
(
ω
k
1
2
+
ω
k
2
2
+
⋯
+
ω
k
n
2
)
=
σ
k
1
2
+
σ
k
2
2
+
⋯
+
σ
k
n
2
=
T
r
(
P
k
)
\begin{matrix} J_k=E(\omega_{k1}^2+\omega_{k2}^2+\dots+\omega_{kn}^2)\\=\sigma_{k1}^2+\sigma_{k2}^2+\dots+\sigma_{kn}^2\\=\rm Tr(\bm P_k)\end{matrix}
Jk=E(ωk12+ωk22+⋯+ωkn2)=σk12+σk22+⋯+σkn2=Tr(Pk)
- P k = E ( ω k ω k T ) \bm P_k=E(\bm\omega_k\bm\omega_k^{\rm T}) Pk=E(ωkωkT): ω k \bm \omega_k ωk在 k k k时刻的协方差矩阵, 为对称矩阵, 对角项是各误差的方差, 即 J k J_k Jk可表达为 T r ( P k ) \rm Tr(\bm P_k) Tr(Pk)
- 展开并考虑状态估计误差
ω
k
−
1
\bm\omega_{k-1}
ωk−1与测量噪声
v
k
−
1
\bm v_{k-1}
vk−1相互独立, 且为零均值噪声, 得估计误差的协方差递推公式
P
k
=
(
I
−
K
k
C
)
P
k
−
1
(
I
−
K
k
C
)
T
+
K
k
R
K
k
T
\bm P_k=(\bm I-\bm K_k\bm C)\bm P_{k-1}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_{k}^{\rm T}
Pk=(I−KkC)Pk−1(I−KkC)T+KkRKkT
- R \bm R R: 测量误差 v \bm v v的协方差, 即当前 k k k时刻估计误差协方差 P k \bm P_k Pk与上一时刻协方差 P k − 1 \bm P_{k-1} Pk−1及测量误差协方差 R \bm R R有关
- 对迹求偏导: ∂ J k ∂ K k = ∂ T r ( P k ) ∂ K k = 0 \frac{\partial J_k}{\partial\bm K_k}=\frac{\partial{\rm Tr}(\bm P_k)}{\partial\bm K_k}=0 ∂Kk∂Jk=∂Kk∂Tr(Pk)=0
- 得最优 K k = P k − 1 C T ( R + C P k − 1 C T ) − 1 \bm K_k={\bm P_{k-1}\bm C^{\rm T}(\bm R+\bm C\bm P_{k-1}\bm C^{\rm T})^{-1}} Kk=Pk−1CT(R+CPk−1CT)−1
- 代价函数
J
k
=
E
(
ω
k
1
2
+
ω
k
2
2
+
⋯
+
ω
k
n
2
)
=
σ
k
1
2
+
σ
k
2
2
+
⋯
+
σ
k
n
2
=
T
r
(
P
k
)
\begin{matrix} J_k=E(\omega_{k1}^2+\omega_{k2}^2+\dots+\omega_{kn}^2)\\=\sigma_{k1}^2+\sigma_{k2}^2+\dots+\sigma_{kn}^2\\=\rm Tr(\bm P_k)\end{matrix}
Jk=E(ωk12+ωk22+⋯+ωkn2)=σk12+σk22+⋯+σkn2=Tr(Pk)
- 最小二乘估计的计算流程
- 确定初始钻杆太最优估计值 x ^ 0 \hat{\bm x}_0 x^0与估计值协方差 P 0 \bm P_0 P0
- 当对系统状态 x \bm x x完全不了解, 可将 x 0 ^ \hat{\bm x_0} x0^设为任意值, P 0 = ∞ I \bm P_0=\infty \bm I P0=∞I(可信度极低)
- 当对 x 0 ^ \hat{\bm x_0} x0^非常确定, 可令 P 0 = 0 \bm P_0=0 P0=0
- 开始运行时刻 k = 1 k=1 k=1, 到时刻 k k k时
- K k = P k − 1 C T ( R + C P k − 1 C T ) − 1 x ^ k = x ^ k − 1 + K k ( y k − C x ^ k − 1 ) P k = ( I − K k C ) P k − 1 ( I − K k C ) T + K k R K k T \begin{matrix} {\bm K}_k={\bm P}_{k-1}{\bm C}^{\rm T}(\bm R+{\bm C}{\bm P}_{k-1}{\bm C}^{\rm T})^{-1} \\ \hat{\bm x}_k=\hat{\bm x}_{k-1}+{\bm K}_k(\bm y_k-{\bm C}\hat{x}_{k-1}) \\ {\bm P}_k=(\bm I-\bm K_k\bm C){\bm P}_{k-1}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_k^{\rm T} \end{matrix} Kk=Pk−1CT(R+CPk−1CT)−1x^k=x^k−1+Kk(yk−Cx^k−1)Pk=(I−KkC)Pk−1(I−KkC)T+KkRKkT
- k = 2 , 3 , . . . k=2,3,... k=2,3,...时估计器重复执行步骤, 估计值 x ^ k \hat{\bm x}_k x^k将不断逼近真实状态 x \bm x x
5.3.状态向量和协方差随时间变化
- 在离散状态空间模型增加过程噪声
w
w
w:
x
k
=
A
x
k
−
1
+
B
u
k
−
1
+
w
k
−
1
{\bm x}_k={\bm A\bm x}_{k-1}+{\bm B\bm u}_{k-1}+{\bm w}_{k-1}
xk=Axk−1+Buk−1+wk−1
- 过程噪声期望为0: P k = E ( ω k ω k T ) = [ ( x k − x k ‾ ) ( x k − x k ‾ ) T ] = A x ‾ k − 1 + B u k − 1 {\bm P_k}=E(\bm \omega_k\bm\omega_k^{\rm T})=[(\bm x_k-\overline{\bm x_k})(\bm x_k-\overline{\bm x_k})^{\rm T}]={\bm A}\overline{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1} Pk=E(ωkωkT)=[(xk−xk)(xk−xk)T]=Axk−1+Buk−1
-
P
k
=
A
P
k
−
1
A
T
+
Q
\bm P_k=\bm A\bm P_{k-1}\bm A^{\rm T}+\bm Q
Pk=APk−1AT+Q
- 当前时刻
k
k
k的状态向量协方差
P
k
\bm P_k
Pk与
P
k
−
1
\bm P_{k-1}
Pk−1及过程噪声协方差
Q
\bm Q
Q有关.
- Q \bm Q Q只和系统有关, 与时间无关
- 当前时刻
k
k
k的状态向量协方差
P
k
\bm P_k
Pk与
P
k
−
1
\bm P_{k-1}
Pk−1及过程噪声协方差
Q
\bm Q
Q有关.
6.离散卡尔曼滤波器
- 已知白噪声的协方差矩阵
Q
R
\bm Q\bm R
QR和各个时刻测量值的条件
y
\bm y
y, 估计系统在当前k时刻最优状态向量
-
{
x
k
=
A
x
k
−
1
+
B
u
k
−
1
+
w
k
−
1
y
k
=
C
x
k
+
v
k
\left\{\begin{matrix} {\bm x}_k={\bm A}{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}+{\bm w}_{k-1} \\ {\bm y}_k={\bm C\bm x}_k+{\bm v}_k \end{matrix}\right.
{xk=Axk−1+Buk−1+wk−1yk=Cxk+vk
- 过程噪声 w \bm w w和测量噪声 v \bm v v都是零均值且不相关的白噪声 w ∼ ( 0 , Q ) , v ∼ ( 0 , R ) {\bm w}\sim(0,\bm Q), {\bm v}\sim(0,\bm R) w∼(0,Q),v∼(0,R)
-
{
x
k
=
A
x
k
−
1
+
B
u
k
−
1
+
w
k
−
1
y
k
=
C
x
k
+
v
k
\left\{\begin{matrix} {\bm x}_k={\bm A}{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}+{\bm w}_{k-1} \\ {\bm y}_k={\bm C\bm x}_k+{\bm v}_k \end{matrix}\right.
{xk=Axk−1+Buk−1+wk−1yk=Cxk+vk
- 先验估计 x ^ k − \hat{\bm x}_{k}^{-} x^k−: 只用 1 → ( k − 1 ) 1\rightarrow(k-1) 1→(k−1) 的测量值 y \bm y y估计 x k \bm x_k xk
- x ^ k − = E { x k ∣ y 1 , y 2 , … , y k − 1 } \hat{\bm x}_{k}^{-}=E\{\bm x_k | \bm y_1,\bm y_2,\dots,\bm y_{k-1}\} x^k−=E{xk∣y1,y2,…,yk−1}
- 先验协方差 P k − = E [ ( x k − x ^ k − ) ( x k − x ^ k − ) ] \bm P_k^{-}=E[({\bm x}_k-\hat{\bm x}_k^{-})(\bm x_k-\hat{\bm x}_k^{-})] Pk−=E[(xk−x^k−)(xk−x^k−)]
- 后验估计 x ^ k + \hat{\bm x}_{k}^{+} x^k+: 用 1 → ( k ) 1\rightarrow(k) 1→(k) 的测量值 y \bm y y估计 x k \bm x_k xk
- x ^ k + = E { x k ∣ y 1 , y 2 , … , y k − 1 , y k } \hat{\bm x}_{k}^{+}=E\{\bm x_k | \bm y_1,\bm y_2,\dots,\bm y_{k-1},\bm y_{k}\} x^k+=E{xk∣y1,y2,…,yk−1,yk}
- 后验协方差 P k + = E [ ( x k − x ^ k + ) ( x k − x ^ k + ) ] \bm P_k^{+}=E[({\bm x}_k-\hat{\bm x}_k^{+})(\bm x_k-\hat{\bm x}_k^{+})] Pk+=E[(xk−x^k+)(xk−x^k+)]
利用的测量值越多, 估计精度越高, 后验估计比先验估计更接近状态向量的真实值, 后验协方差<先验协方差
- 卡尔曼滤波器
- 从
x
^
k
−
1
+
\hat{\bm x}_{k-1}^{+}
x^k−1+到
x
^
k
−
\hat{\bm x}_{k}^{-}
x^k−, 时间前进一步, 但无新观测值, 均为
1
→
(
k
−
1
)
1\rightarrow(k-1)
1→(k−1)的观测值
- { x ^ k − = A x ^ k − 1 + + B u k − 1 P k − = A P k − 1 + A T + Q \left\{\begin{matrix} \hat{\bm x}_k^-=\bm A\hat{\bm x}_{k-1}^++{\bm B}{\bm u}_{k-1} \\ {\bm P}_k^-={\bm A}{\bm P}_{k-1}^+{\bm A}^{\rm T}+{\bm Q} \end{matrix}\right. {x^k−=Ax^k−1++Buk−1Pk−=APk−1+AT+Q 以上一时刻后验计算当前时刻先验
- 得到新观测值后可以计算当前时刻后验
-
{
K
k
=
P
k
−
C
T
(
R
+
C
P
k
−
C
T
)
−
1
x
^
k
+
=
x
^
k
−
+
K
k
(
y
k
−
C
x
^
k
−
)
P
k
+
=
(
I
−
K
k
C
)
P
k
−
(
I
−
K
k
C
)
T
+
K
k
R
K
k
T
\left\{\begin{matrix} {\bm K}_k={\bm P}_{k}^{-}{\bm C}^{\rm T}(\bm R+{\bm C}{\bm P}_{k}^{-}{\bm C}^{\rm T})^{-1} \\ \hat{\bm x}_k^{+}=\hat{\bm x}_{k}^{-}+{\bm K}_k(\bm y_k-{\bm C}\hat{x}_{k}^{-}) \\ {\bm P}_k^{+}=(\bm I-\bm K_k\bm C){\bm P}_{k}^{-}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_k^{\rm T} \end{matrix}\right.
⎩
⎨
⎧Kk=Pk−CT(R+CPk−CT)−1x^k+=x^k−+Kk(yk−Cx^k−)Pk+=(I−KkC)Pk−(I−KkC)T+KkRKkT
- K k \bm K_k Kk:卡尔曼滤波增益, x k + ^ \hat{\bm x_k^+} xk+^:后验估计即k时刻最优估计
-
{
K
k
=
P
k
−
C
T
(
R
+
C
P
k
−
C
T
)
−
1
x
^
k
+
=
x
^
k
−
+
K
k
(
y
k
−
C
x
^
k
−
)
P
k
+
=
(
I
−
K
k
C
)
P
k
−
(
I
−
K
k
C
)
T
+
K
k
R
K
k
T
\left\{\begin{matrix} {\bm K}_k={\bm P}_{k}^{-}{\bm C}^{\rm T}(\bm R+{\bm C}{\bm P}_{k}^{-}{\bm C}^{\rm T})^{-1} \\ \hat{\bm x}_k^{+}=\hat{\bm x}_{k}^{-}+{\bm K}_k(\bm y_k-{\bm C}\hat{x}_{k}^{-}) \\ {\bm P}_k^{+}=(\bm I-\bm K_k\bm C){\bm P}_{k}^{-}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_k^{\rm T} \end{matrix}\right.
⎩
⎨
⎧Kk=Pk−CT(R+CPk−CT)−1x^k+=x^k−+Kk(yk−Cx^k−)Pk+=(I−KkC)Pk−(I−KkC)T+KkRKkT
- 从
x
^
k
−
1
+
\hat{\bm x}_{k-1}^{+}
x^k−1+到
x
^
k
−
\hat{\bm x}_{k}^{-}
x^k−, 时间前进一步, 但无新观测值, 均为
1
→
(
k
−
1
)
1\rightarrow(k-1)
1→(k−1)的观测值
离散卡尔曼滤波器计算流程
类似最小二乘估计
- 先给出初始状态最优状态估计值 x ^ 0 + \hat{\bm x}_0^+ x^0+与协方差 P 0 + \bm P_0^+ P0+(由可信度决定)
- 开始运行到时刻k=1, 先计算先验估计与先验方差
- { x ^ k − = A x ^ k − 1 + + B u k − 1 P k − = A P k − 1 + A T + Q \left\{\begin{matrix} \hat{\bm x}_k^-=\bm A\hat{\bm x}_{k-1}^++{\bm B}{\bm u}_{k-1} \\ {\bm P}_k^-={\bm A}{\bm P}_{k-1}^+{\bm A}^{\rm T}+{\bm Q} \end{matrix}\right. {x^k−=Ax^k−1++Buk−1Pk−=APk−1+AT+Q
- 计算卡尔曼滤波增益
- K k = P k − C T ( R + C P k − C T ) − 1 {\bm K}_k={\bm P}_{k}^{-}{\bm C}^{\rm T}(\bm R+{\bm C}{\bm P}_{k}^{-}{\bm C}^{\rm T})^{-1} Kk=Pk−CT(R+CPk−CT)−1
- 读取各个传感器测量值带入矩阵得 y k \bm y_k yk, 在计算后验估计和后验协方差
- { x ^ k + = x ^ k − + K k ( y k − C x ^ k − ) P k + = ( I − K k C ) P k − ( I − K k C ) T + K k R K k T \left\{\begin{matrix} \hat{\bm x}_k^{+}=\hat{\bm x}_{k}^{-}+{\bm K}_k(\bm y_k-{\bm C}\hat{x}_{k}^{-}) \\ {\bm P}_k^{+}=(\bm I-\bm K_k\bm C){\bm P}_{k}^{-}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_k^{\rm T} \end{matrix}\right. {x^k+=x^k−+Kk(yk−Cx^k−)Pk+=(I−KkC)Pk−(I−KkC)T+KkRKkT
- k = 2 , 3 , … k=2,3,\dots k=2,3,…重复执行步骤
7.测量协方差
- 离散卡尔曼滤波器中要确定: 过程噪声协方差
Q
\bm Q
Q, 测量噪声协方差
R
\bm R
R(每次读取测量值的协方差,较容易确定)
- 如果要保存大量测量值, 内存不够, 需要一种逐步递推得均值和协方差计算方法
7.1.平均值与协方差得递推公式
- 均值 x ‾ n = x ‾ n − 1 + x n − x ‾ n − 1 n \overline{\bm x}_n=\overline{\bm x}_{n-1}+\frac{{\bm x}_n-\overline{\bm x}_{n-1}}{n} xn=xn−1+nxn−xn−1
- 协方差 C n = n − 1 n 2 ( x n − x ‾ n − 1 ) ( x n − x ‾ n − 1 ) T + n − 1 n C n {\bm C_n}=\frac{n-1}{n^2}({\bm x}_n-\overline{\bm x}_{n-1})({\bm x}_n-\overline{\bm x}_{n-1})^{\rm T}+\frac{n-1}{n}{\bm C}_n Cn=n2n−1(xn−xn−1)(xn−xn−1)T+nn−1Cn
7.2.测量四足机器人传感器协方差
- 静止状态时, 测量噪声 v \bm v v协方差 R \bm R R=测量值 y \bm y y的协方差 C y = 1 n ∑ k = 1 n v k v k T = R \bm C_y=\frac{1}{n}\sum_{k=1}^n{\bm v_k}{\bm v}_k^{\rm T}={\bm R} Cy=n1∑k=1nvkvkT=R
- 递推方法求得 R \bm R R和 C u \bm C_u Cu
- 过程噪声协方差
Q
\bm Q
Q包含输入量噪声协方差
C
u
\bm C_u
Cu, 只考虑输入量噪声
- x k = A x k − 1 + B u k − 1 + w k − 1 = A x k − 1 + B ( u k − 1 + o k − 1 ) = A x k − 1 + B u k − 1 + B o k − 1 \begin{matrix} {\bm x}_k={\bm A}{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}+{\bm w}_{k-1} \\ ={\bm A}{\bm x}_{k-1}+{\bm B}({\bm u}_{k-1}+{\bm o}_{k-1}) \\ ={\bm A}{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}+{\bm B}{\bm o}_{k-1} \end{matrix} xk=Axk−1+Buk−1+wk−1=Axk−1+B(uk−1+ok−1)=Axk−1+Buk−1+Bok−1
- Q u = B C u B T \bm Q_u={\bm B}{\bm C_u}{\bm B}^{\rm T} Qu=BCuBT
8.离散卡尔曼滤波调参
8.1.协方差
- 若给过程噪声协方差
Q
Q
Q, 测量噪声协方差
R
R
R, 初始最优估计协方差
P
0
+
P_0^+
P0+乘相同的系数a, 离散克尔曼滤波器的计算结果不变
- 可任意等比例缩放协方差矩阵, 使其处于方便计算的数量级
- 离散卡尔曼滤波器包含了一个状态空间模型, 可认为其将自己的状态空间模型估计的状态与测量值估计的状态进行"加权最小二乘估计", 权重为Q,R
- Q↓: 不信任状态空间模型, 若精度较差则结果出错
- Q↑: R↓, 过度信任测量值, 若测量噪声较大则估计也有大噪声, 状态向量有高频振动
- 调试Q:为保证估计结果无太大错误,先给较大的Q, 若产生高频振动则逐渐减小
8.2.腾空&触地
- 状态空间模型的足端位置基于足端触地, 腾空时 Q → ∞ Q\rightarrow \infty Q→∞, 触地时缩小 Q Q Q
- 可变协方差: 分段函数:
σ
(
x
)
{
x
w
r
x
<
w
r
1
w
r
≤
x
≤
1
−
w
r
1
−
x
w
r
x
>
1
−
w
r
\sigma (x)\left\{\begin{matrix} \frac{x}{w_r} & x<w_r\\ 1 & w_r\le x\le 1-w_r\\ \frac{1-x}{w_r} & x>1-w_r\end{matrix}\right.
σ(x)⎩
⎨
⎧wrx1wr1−xx<wrwr≤x≤1−wrx>1−wr
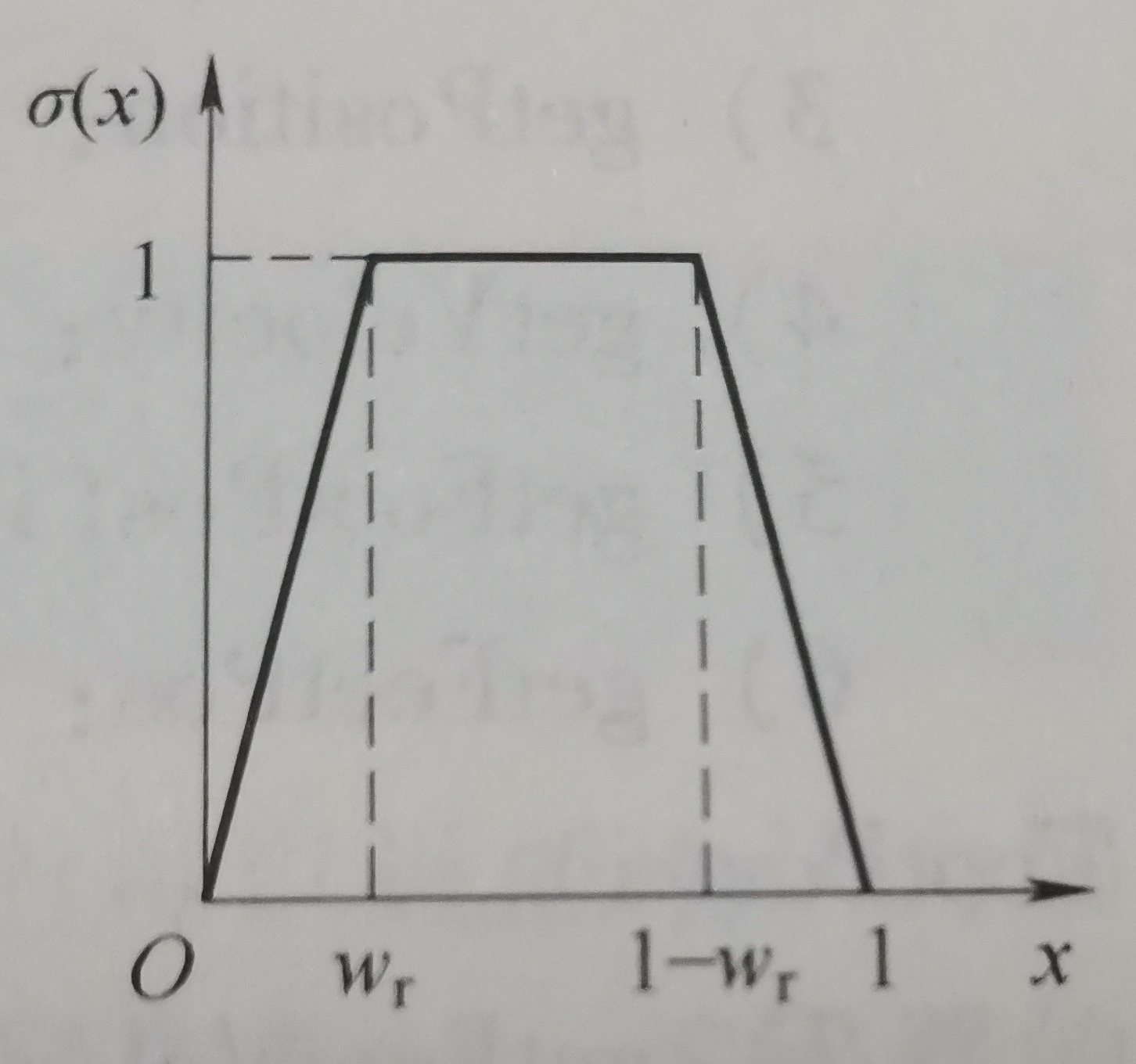
- C s t a n c e = [ 1 + ( 1 − σ ) L ] C i n i t C_{stance}=[1+(1-\sigma)L]C_{init} Cstance=[1+(1−σ)L]Cinit , C i n i t C_{init} Cinit稳定触地时的噪声协方差矩阵
- 腾空时的位置由正运动学算得
ref
<四足机器人控制算法-建模,控制与实践>



![[进阶]TCP通信实现BS架构,网站开发的原理,线程池优化BS架构](https://img-blog.csdnimg.cn/04ac05ba6af04765ae57f5860668a7e9.png)