Antialiasing(反走样)

继续上节课：检测一个像素中心是否在三角形内部。
如果一个像素的中心在三角形内部，那么我们就将该三角形涂成红色：
我们就可以得到如下图所示的结果，但是会出现非常严重的锯齿现象。

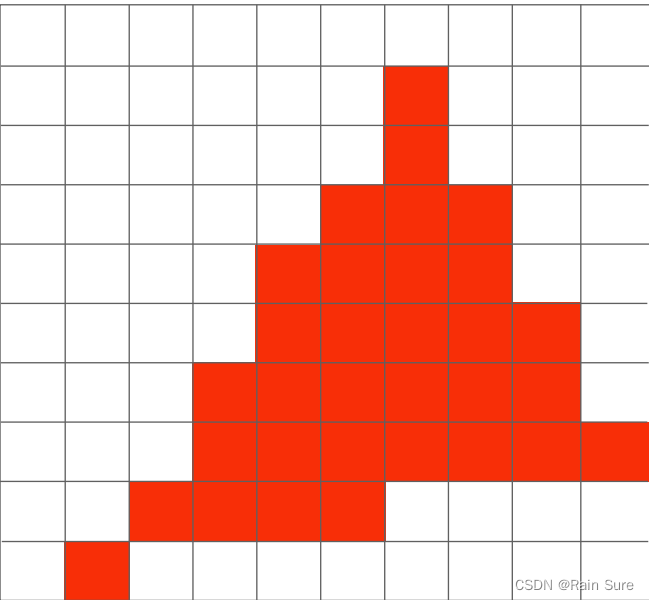
我们并不希望出现这么严重的锯齿，这就是本节课要讲的内容——反走样。

Sampling is Ubiquitous in Computer Graphics(采样在计算机图形学中无处不在)

• 光栅化 = 在二维坐标中的采样
• 照片 = 采样图像传感器平面
• 视频 = 在时间上采样

Sampling Artifacts(Errors or Mistakes or Inaccuracies) in Computer Graphics(在计算机图形学中采样的瑕疵)

Jaggies(Staircase Pattern)锯齿

这是采样中的一种Artifacts

Moire Pattern in Imaging(摩尔纹)

去掉奇数行和奇数列，再将图片放大到原来的大小，就会出现。

Wagon Wheel Illusion(False Motion)车轮错觉

人眼在时间上的采样跟不上速度就会出现这种情况：

在走样背后的本质是什么呢？

Signal are changing too fast (high frequency), but sampled too slowly
信号变化的太快，而采样的频率不够高。

Antialiasing Idea: Blurring (Pre-Filtering) Before Sampling(采样之前进行模糊)

先对三角形进行模糊，再进行采样，采样出是什么颜色就是什么颜色。

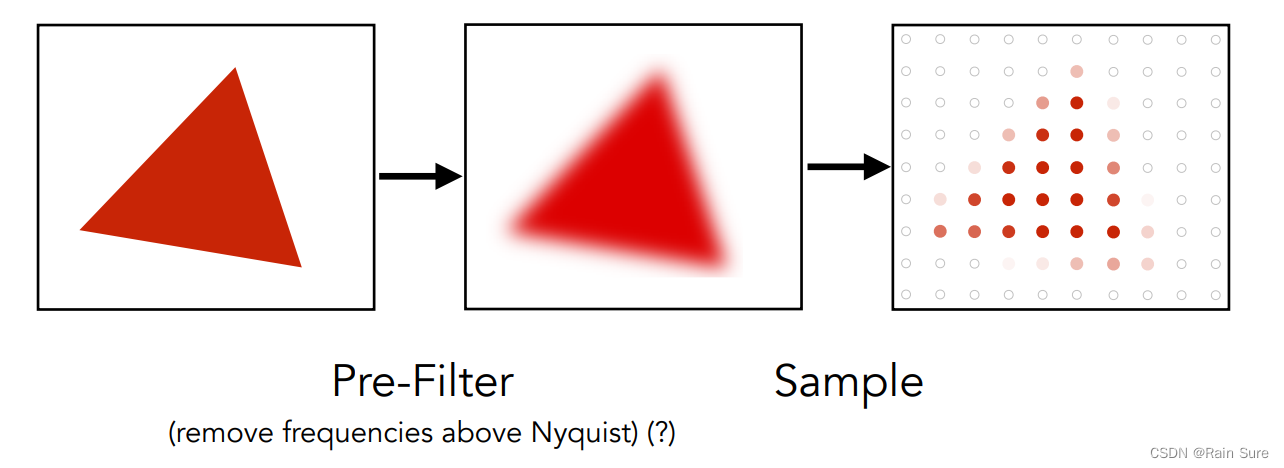
如果先去采样再去滤波，结果就是错误的！(Blurred Aliased)

But Why?

1. 为什么采样的速度跟不上信号的速度就是走样？
2. 为什么先进行滤波再进行采样可以达到反走样？

Frequency Domain(频域)

Sines and Cosines(正弦和余弦)

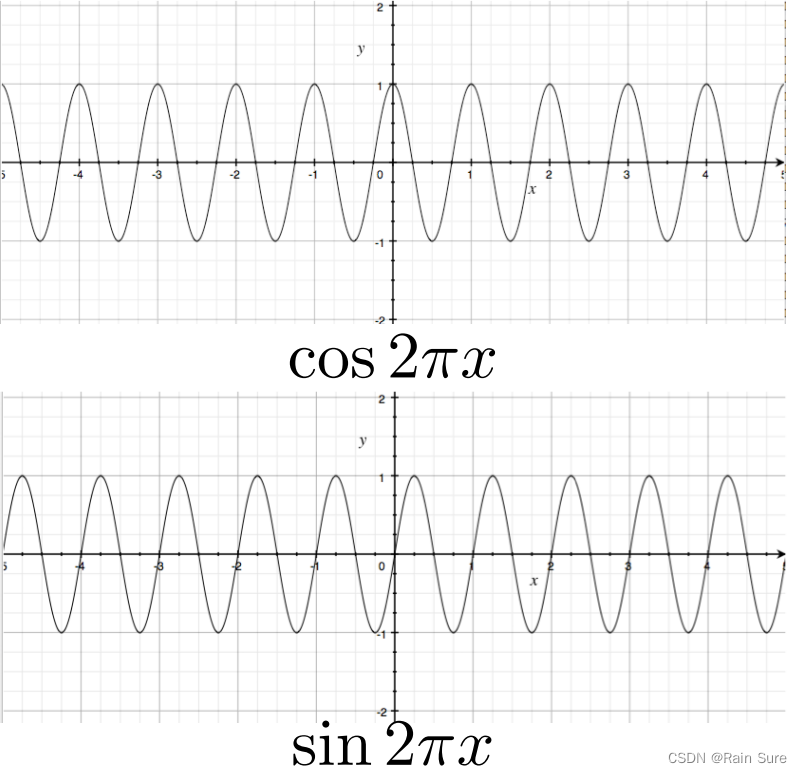
通过调整$x$前面的系数，影响频率：

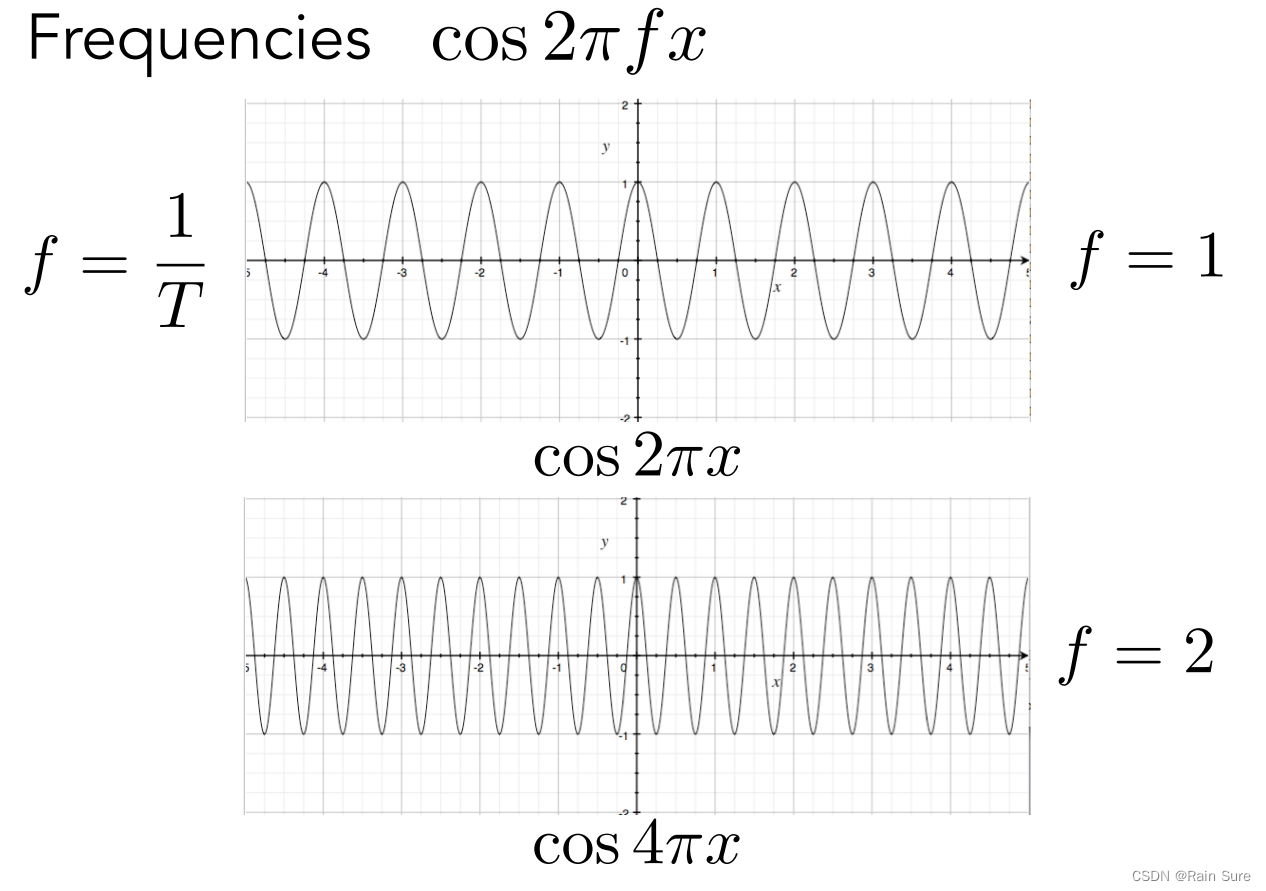
傅里叶级数展开

任何一个周期函数，都可以把它写成一系列正弦函数和余弦函数的线性组合。

傅里叶变换与逆变换

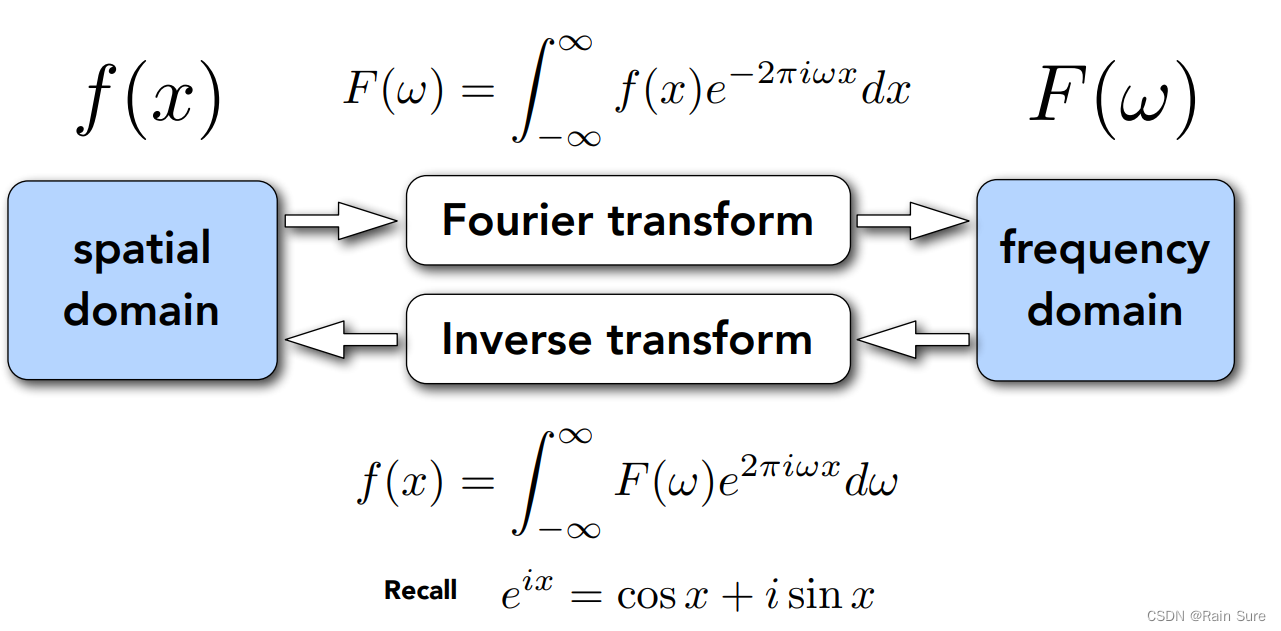
更高的频率需要更快的采样：

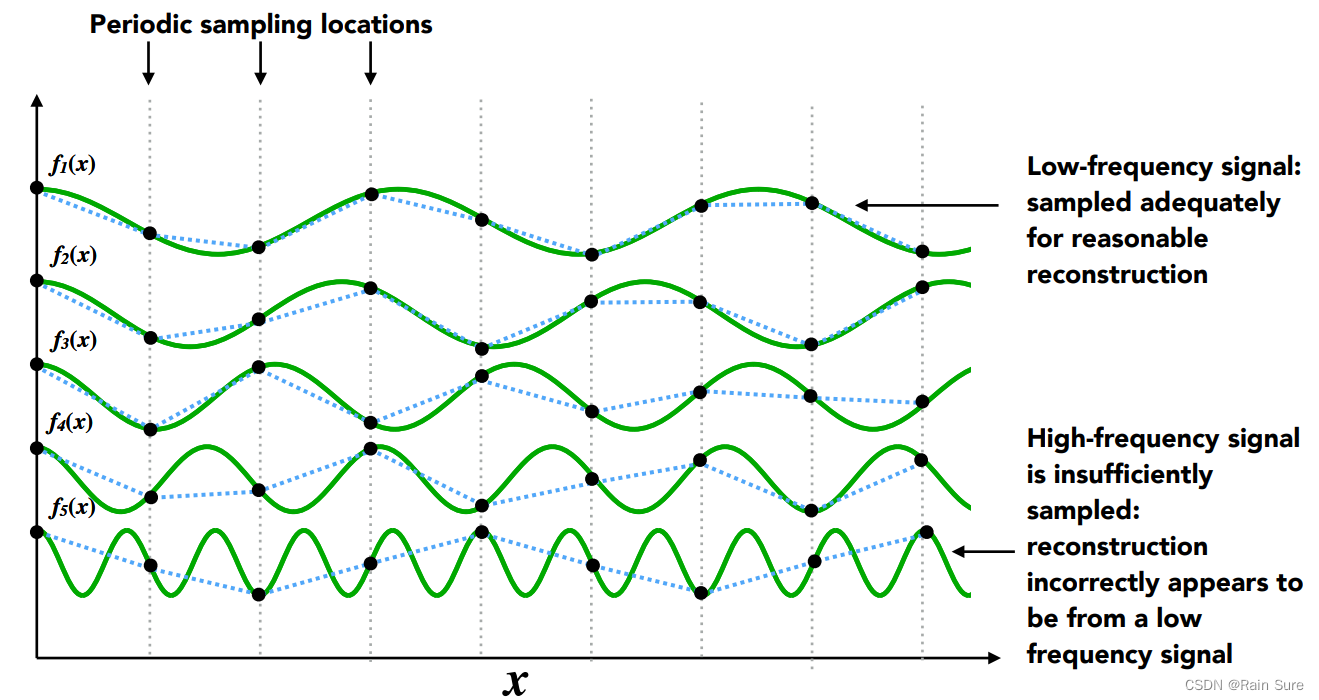
同样的一种采样方法采样两种频率不同的函数，得出来的结果我们无法区别，这就是走样！

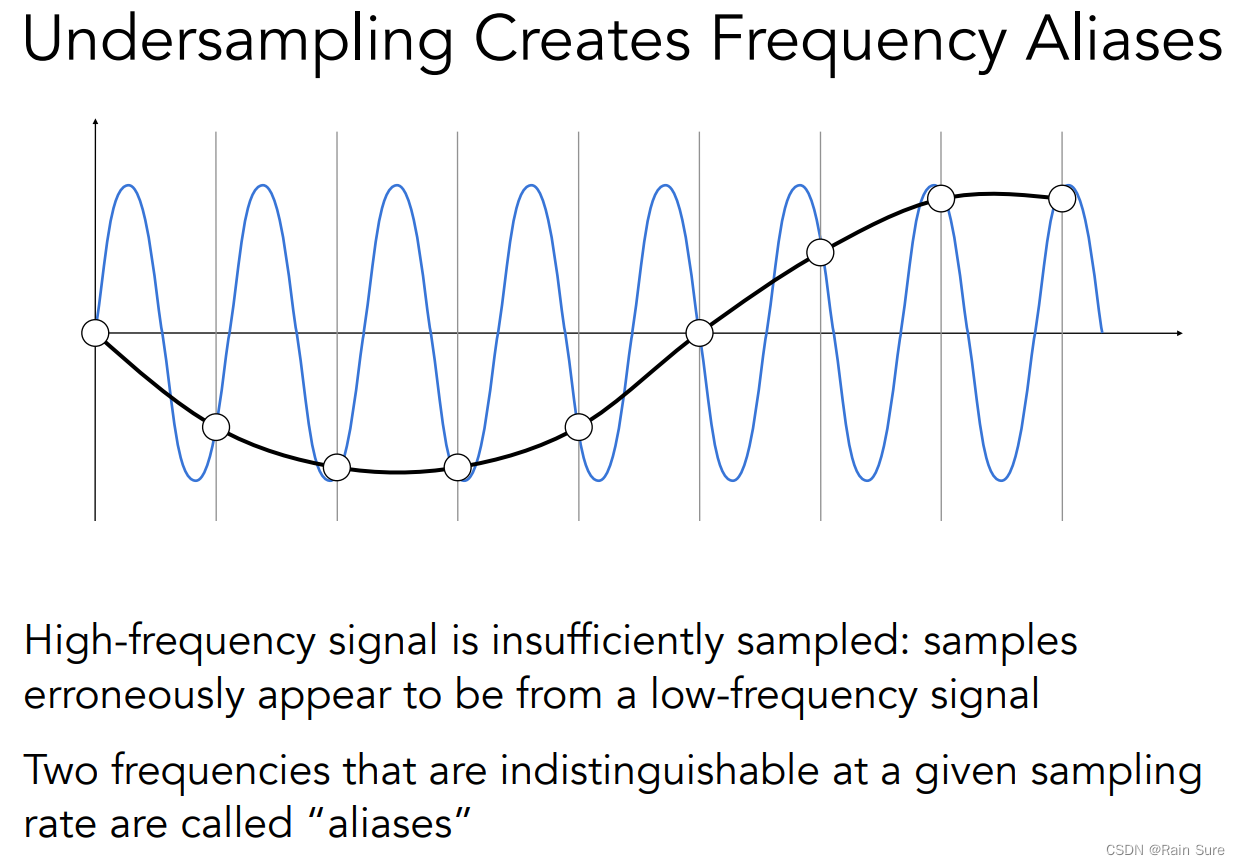
Filtering = Getting rid of certain frequency contents(滤波 = 删掉某些特定的频率内容)

傅里叶变换可以把一个图像从时域变到频域：

过滤掉低频部分（边缘滤波）：高通滤波

过滤掉高频部分（模糊滤波）: 低通滤波

同时去掉低频和高频：

Filtering = Convolution( = Averaging) 滤波 = 卷积（平均）

卷积

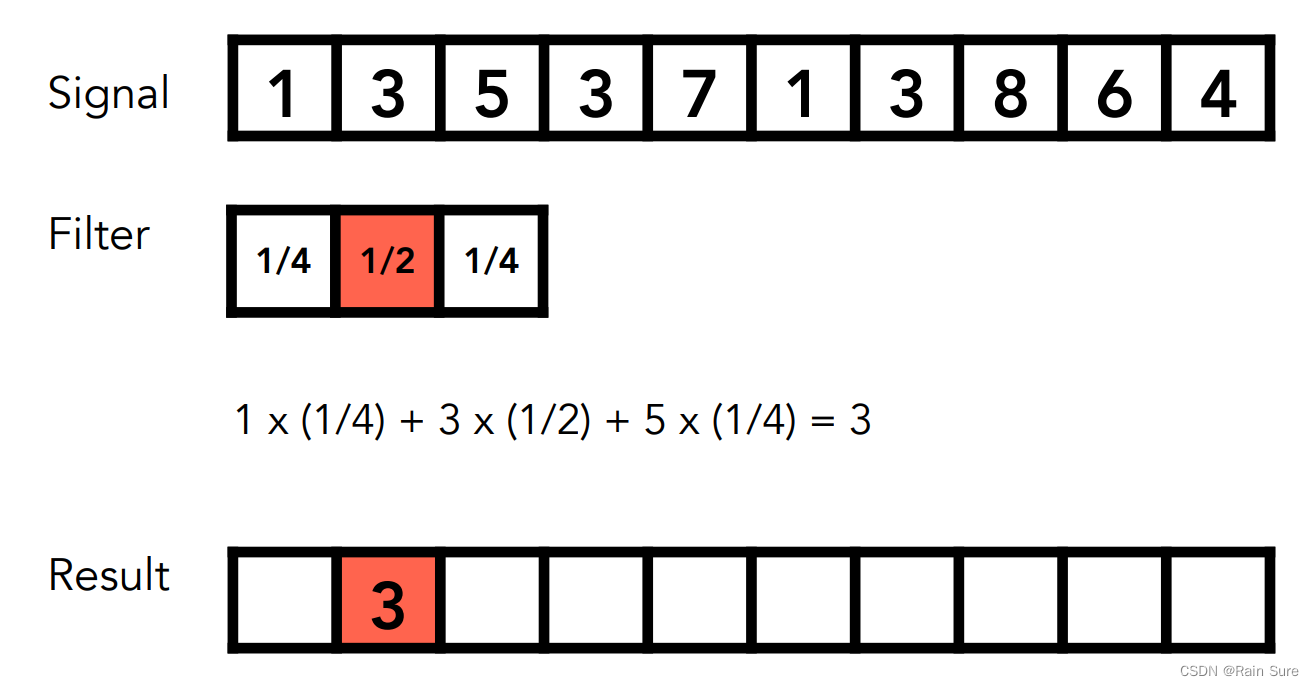
卷积定理

空间中的卷积等于频域中的乘法，反之亦然。
时域的卷积等于频域的乘积。

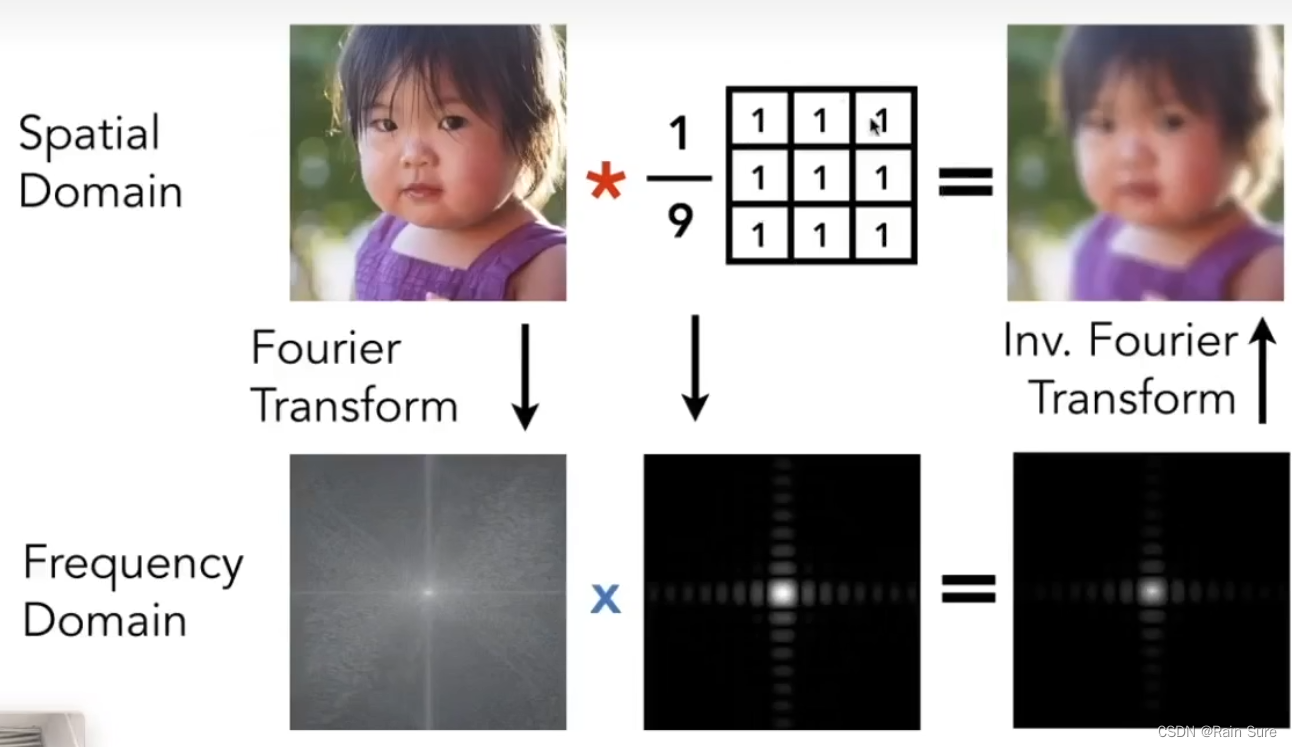
Sampling = Repeating Frequency Contents(采样就是在重复频域上的内容)

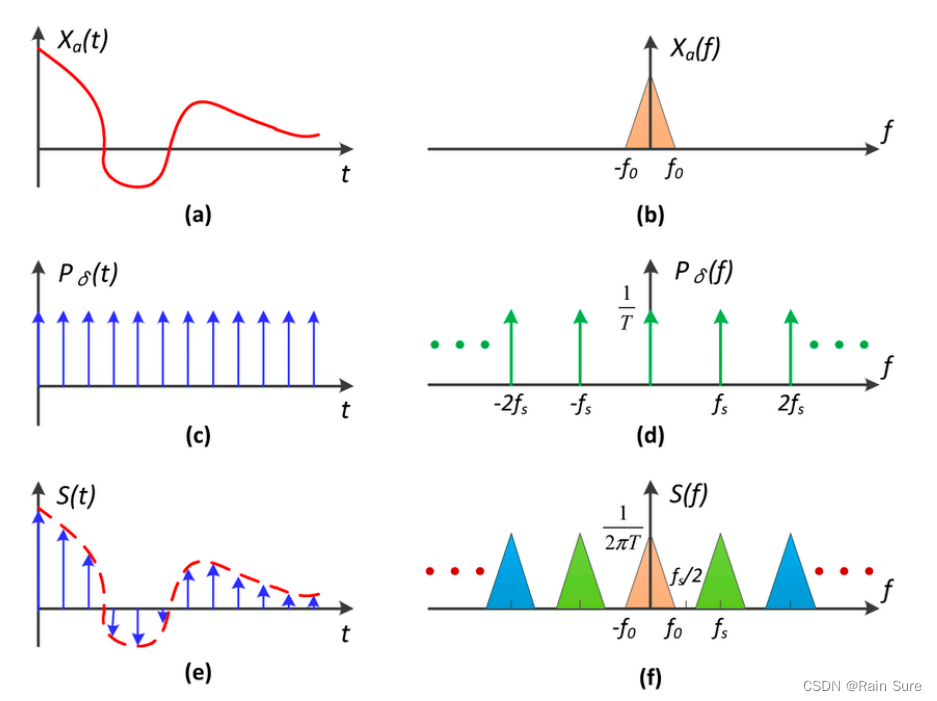
走样：频率内容交叉

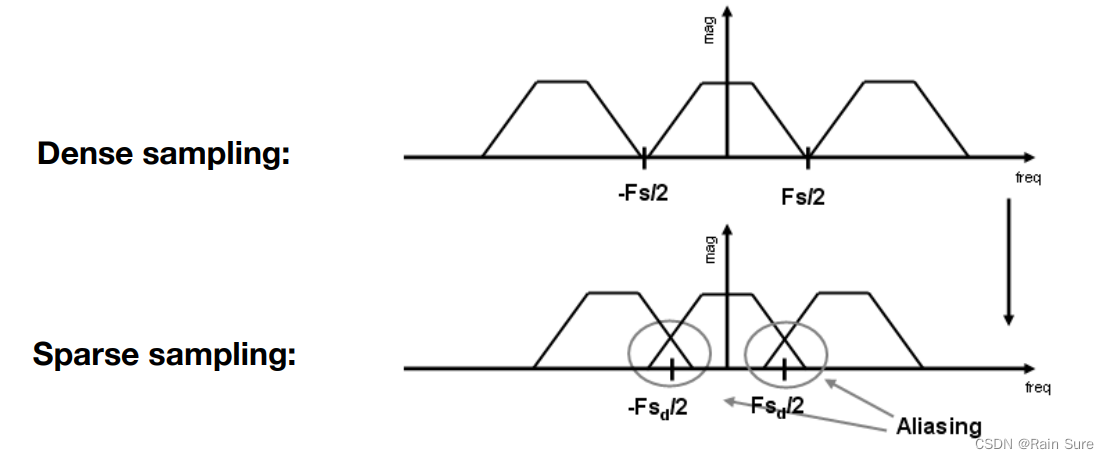
How Can We Reduce Aliasing Error?

方法1：增加采样率

• 本质上是增加了傅立叶域中副本之间的距离
• 高分辨率设备，传感器，帧缓冲器
• 但是：增加了消耗

方法2：反走样

• 在重复之前使傅里叶内容“更窄”
• 也就是说：在采样之前过滤掉高频部分
  
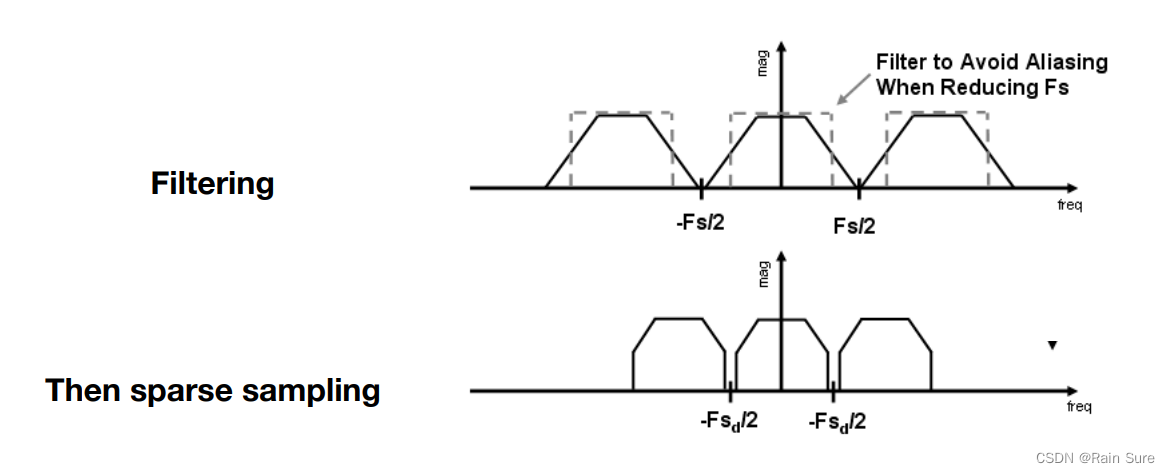
  对于每个像素内部进行一次卷积，求一次平均：
  
  

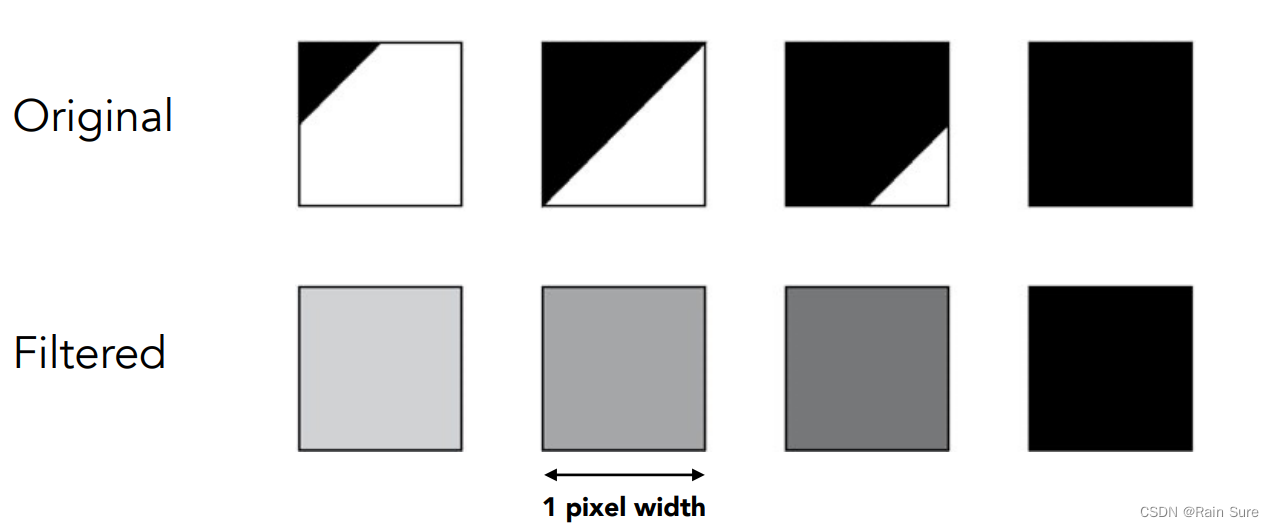
Antialiasing By Supersampling(MSAA)

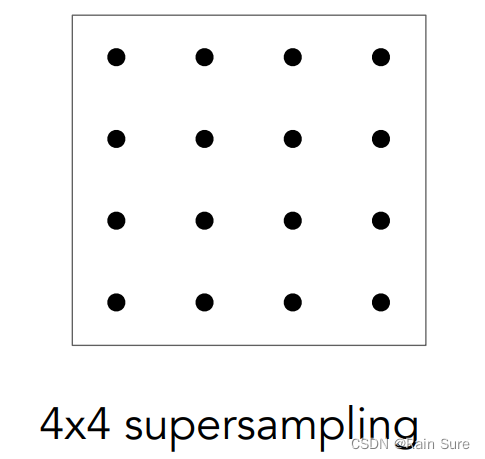
Supersampliing(超采样)

将一个像素细分成许多小像素，然后将每个小的像素的判断结果取平均。

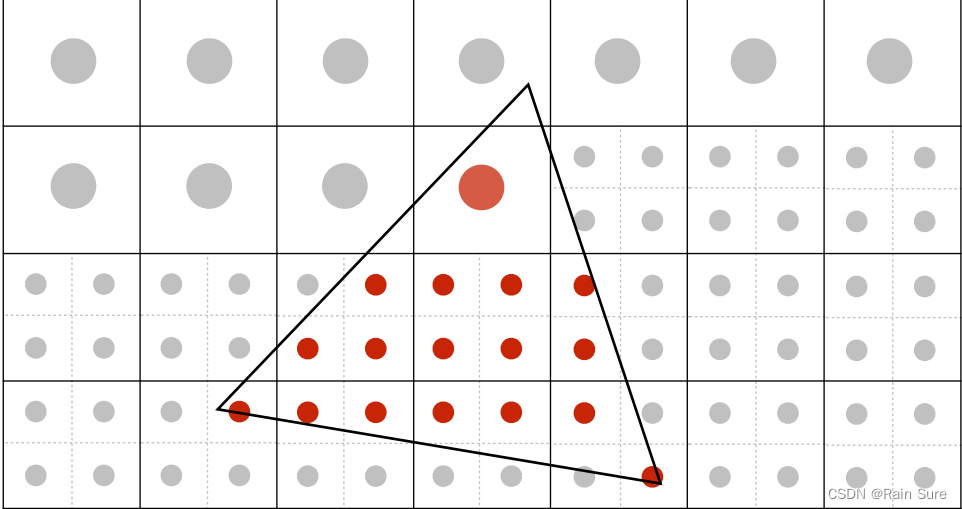
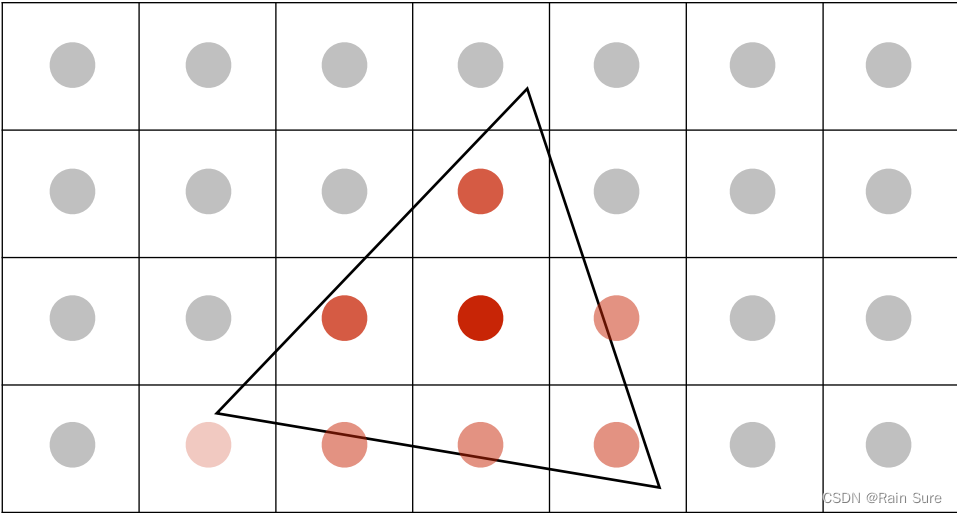
MSAA的代价是什么？

增加了更多的点，增大了计算量。

参考资源

GAMES101 Lecture06