【MATLAB第42期】基于MATLAB的贝叶斯优化决策树分类算法与网格搜索、随机搜索对比，含对机器学习模型的评估度量介绍

网格搜索、随机搜索和贝叶斯优化是寻找机器学习模型参数最佳组合、交叉验证每个参数并确定哪一个参数具有最佳性能的常用方法。

一、 评估指标
1、分类
1.1 准确性
1.2 精度
1.3 召回
1.4 F1值
1.5 F0.5值
1.6 F2值
1.7 计算评估指标的功能
2、回归
2.1 平均绝对误差
2.2 均方误差
2.3 均方根误差
二、 基于F1值执行网格搜索的多循环
三、 fitctree优化选项中的网格搜索（不能将目标函数更改为f1值）
四、 fitctree优化选项中的随机搜索（不能将目标函数更改为f1值）
五、 基于F1值的贝叶斯优化
六、代码获取

在讨论这些方法之前，我想先谈谈评估指标。这是因为从不同的超参数组合中选择最佳模型将是我们的性能指标。

一、 评估指标

这里将讨论不同的评估指标：准确度、精密度、召回率、F1值、F0.5值、F2值、平均绝对误差、均方误差、均方根误差。

1、分类

例如，假设我们的实际标签和预测代码如下：

Actual = {'hi','hi','No hi','hi','No hi','hi','hi','hi','No hi','hi','No hi'};
Prediction = {'hi','No hi','hi','hi','No hi','hi','hi','hi','No hi','No hi','No hi'};
confusionchart(Actual,Prediction);

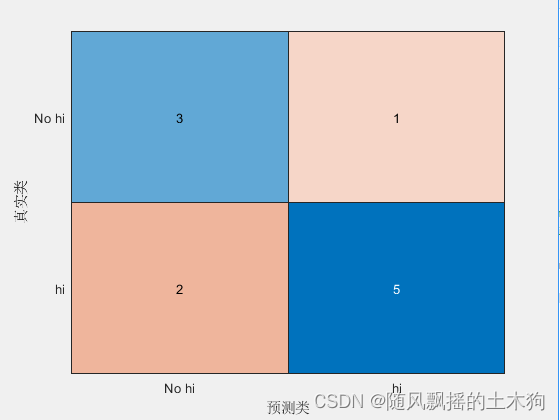
假设“No hi”对我们来说更重要，因此，我们的评估指标（召回率、精度、F1、F2、F0.5）将集中在“No hi“类上。

1.1 准确性

Accuracy = (3+5)/(3+5+2+1)
%Accuracy =0.72727

1.2 精度

Precision = 3 / (3+2)
%Precision = 0.6

1.3 召回

Recall = 3 / (3+1)
%Recall = 0.75

1.4 F1值

它被称为调和均值

F1 = 2*(Precision*Recall)/(Precision+Recall)
%F1=0.6666667

1.5 F0.5值

权重比召回更注重准确性

F05 = (1+0.5^2)*(Precision*Recall)/((0.5^2)*Precision+Recall)
%F05=0.625

1.6 F2值

权重更强调召回而非准确性

F2 = (1+2^2)*(Precision*Recall)/((2^2)*Precision+Recall)
%F2=0.71429

1.7 计算评估指标的功能

您可以下载下面的函数，通过您的输入（实际和预测）在单行中计算所有评估指标
https://www.mathworks.com/matlabcentral/fileexchange/70978-summary_confusion?s_tid=prof_contriblnk

2、回归

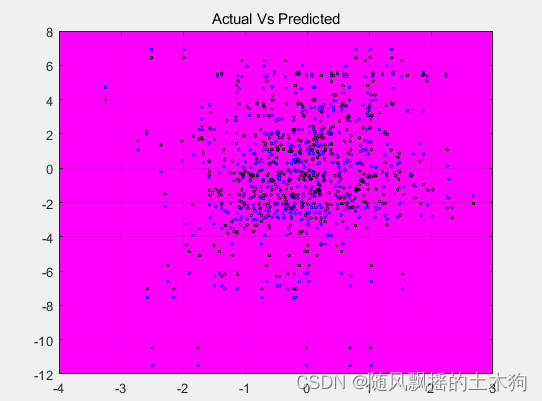
例如，假设我们的预测结果是：

X = randn(100,5);
Actual = X*[1;0;3;0;-1] + randn(100,1);
mdl = fitlm(X,Actual);
Predicted=predict(mdl,X);
plot(X,Actual,'bo','MarkerSize',2)
hold on
plot(X,Predicted,'ko','MarkerSize',2)
title('Actual Vs Predicted')
grid on
set(gca,'Color',[1 0 1])
hold off

2.1 平均绝对误差MAE

MAE = sum(Actual-Predicted)/numel(Actual)
MAE =1.0214e-16

2.2 均方误差MSE

MSE = sum((Actual-Predicted).^2)/numel(Actual)
MSE =0.90475

2.3 均方根误差RMSE

 RMSE = sqrt(sum((Actual-Predicted).^2)/numel(Actual))
RMSE = 0.95118

二、 基于F1值执行网格搜索的多循环

例如，我们将训练具有不同超参数组合的决策树模型。
我们的数据集中有两个类别“b”和“g”，假设类“b”对我们更重要，因此我们将计算b的F1。
超参数的不同组合：
MaxNumSplit : 7,8,9,10
Minimun Leaf : 5,10,15

%导入数据
display(categories(categorical(Y)))
rng(2); % 固定算子
MdlDefault = fitctree(X,Y,'CrossVal','on');
i=1; %初始数量
for MaxNumSplit = 7:1:10
    for MinLeaf = 5:5:15
        Model = fitctree(X,Y,'MaxNumSplits',MaxNumSplit,'MinLeafSize',MinLeaf);        
        
        %计算每个组合的F1
        Predicted=predict(Model,X);
        confMat=confusionmat(Y,Predicted);   
        recall=confMat(1,1)/sum(confMat(1,:));
        precision=confMat(1,1)/sum(confMat(:,1));
        F1(i) = 2*recall*precision/(recall+precision);
        
        %记录当前的MaxNumSplit和Min LeafSize
        MaxNumSplit_r(i) = MaxNumSplit;
        MinLeafSize_r(i) = MinLeaf;
        
        %下一次循环
        i=i+1;
    end
end

%寻找最佳F1值
Best=Final_Result(Final_Result.F1Score==max(Final_Result.F1Score),:)
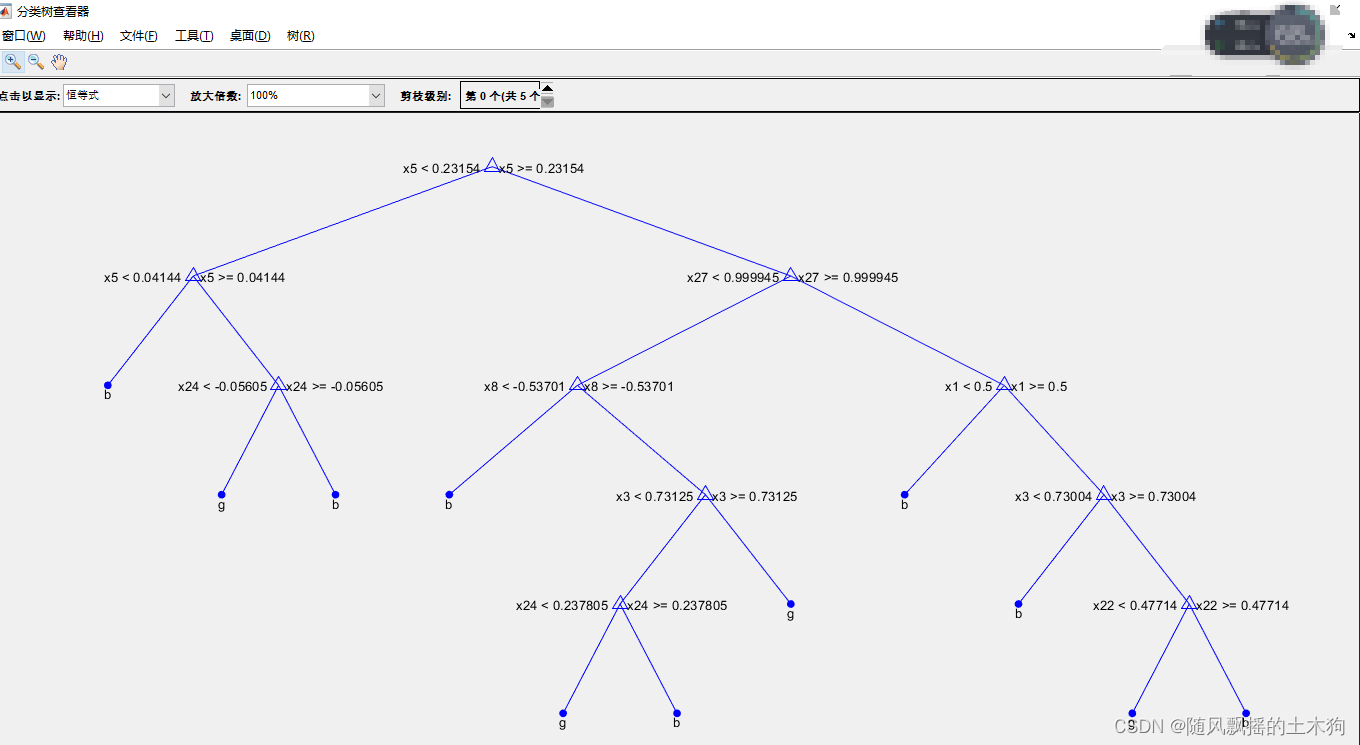
% 训练当前模型
Model = fitctree(X,Y,'MaxNumSplits',Best.MaxNumSplit,'MinLeafSize',Best.MinLeafSize); 

%绘图展示
view(Model,'mode','graph') 

三、 fitctree优化选项中的网格搜索（不能将目标函数更改为f1值）

据我所知，不能改变fitctree中的目标函数
如果您想详细了解fitctree的参数，可以参考以下文档：
https://www.mathworks.com/help/stats/fitctree.html
默认的目标函数是样本误差或交叉验证误差（准确度=1-误差），因此，如果您想将目标函数更改为F1，我建议您使用上面的循环方法。

我用同样的例子来演示如何在fitctree的优化选项中使用网格搜索。

rng(3);%固定算子

%优化变量及其范围
MaxNumSplit = optimizableVariable('MaxNumSplit',[7,10],'Type','integer');
MinLeaf = optimizableVariable('MinLeaf',[5,15],'Type','integer');
hyperparamtersRF = [MaxNumSplit;MinLeaf];

% 执行网格搜索以找到最佳组合
% verbose=1将显示表中的优化结果
Model = fitctree(X,Y,'OptimizeHyperparameters',hyperparamtersRF,'HyperparameterOptimizationOptions',opts);
Accuracy = 1-min(Model.HyperparameterOptimizationResults.Objective)

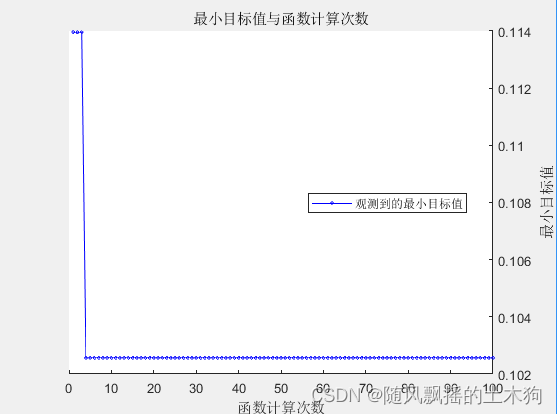
因此，从上表的结果中，我们可以注意到最佳组合是4号（MaxNumSplit=8，MinLeaf=14）。这是网格搜索后选定的模型。

四、 fitctree优化选项中的随机搜索（不能将目标函数更改为f1值）

它与网格搜索相同，不能更改目标函数，默认目标函数基于错误（精度=1-错误）。
因此，您可以考虑基于F1分数进行随机搜索的多循环方法。
如果你想在优化选项中使用随机搜索，你只需要将上面的网格搜索改为随机搜索。

rng(3);%固定算子
% 优化变量及范围
MaxNumSplit = optimizableVariable('MaxNumSplit',[7,10],'Type','integer');
MinLeaf = optimizableVariable('MinLeaf',[5,15],'Type','integer');
hyperparamtersRF = [MaxNumSplit;MinLeaf];

%执行网格搜索以找到最佳组合
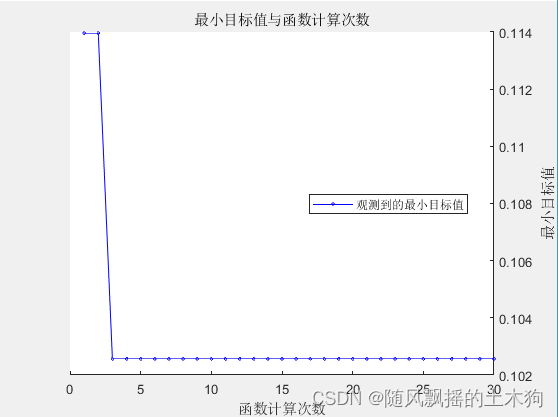
opts = struct('Optimizer','randomsearch','ShowPlots',true,'AcquisitionFunctionName','expected-improvement-plus','verbose',1);
Model = fitctree(X,Y,'OptimizeHyperparameters',hyperparamtersRF,'HyperparameterOptimizationOptions',opts);
Accuracy = 1-min(Model.HyperparameterOptimizationResults.Objective)

五、 基于F1值的贝叶斯优化

本部分展示了如何实现贝叶斯优化，以使用F1值调整决策树的超参数。它还让您了解如何为贝叶斯优化创建目标函数，因此，您可以根据需要更改任何评估矩阵（准确性、精确度、召回率、F1、F2、F0.5）。

rng(3) %固定算子
% 优化变量及范围
MaxNumSplit = optimizableVariable('MaxNumSplit',[7,10],'Type','integer');
MinLeaf = optimizableVariable('MinLeaf',[5,15],'Type','integer');
hyperparamtersRF = [MaxNumSplit;MinLeaf];

%目标功能在辅助功能部分（如下）
%用贝叶斯优化器优化变量
results = bayesopt(@(params)f1_objective(params,X,Y),hyperparamtersRF,...
    'AcquisitionFunctionName','expected-improvement-plus','Verbose',1);

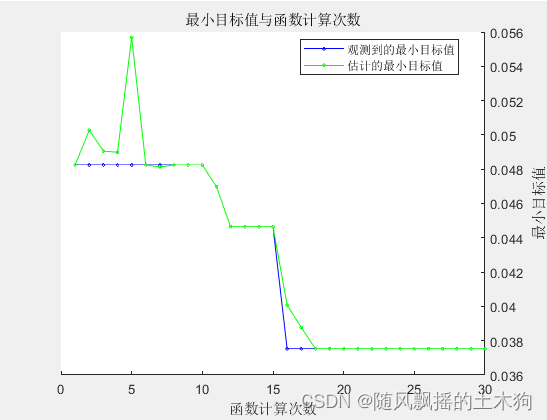
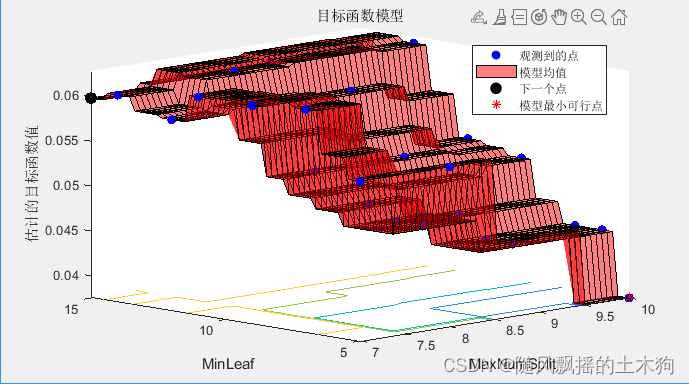
六、代码获取

后台**私信回复“42期”**可获取下载链接。