13.1.概述

最小生成树，包含图的所有顶点的一棵树，树的边采用包含在图中的原有边中权重和最小的边。翻译成人话就是遍历一遍全图所有顶点的最短路径，这条路径就叫最小生成树。

最小生成树存在和图是连通图互为充要条件，顶点都不连通，肯定不可能有路能遍历一遍全图。

求解最小生成树有两种常用算法：

prim算法
kruskal算法

13.2.prim算法

13.2.1.概述

prim算法和Dijkstra算法过程很像，区别在于Dijkstra算法中dist为当前节点到根节点的距离，prim算法中dist为当前节点到树的距离。Dijkstra算法每次是将离根节点最近的节点纳入，prim每次是将离树最近的节点纳入。

Dijkstra算法可以参考博主的上篇文章：数据结构（12）Dijkstra算法JAVA版：图的最短路径问题__BugMan的博客-CSDN博客

13.2.2.代码实现

以遍历下图为例：

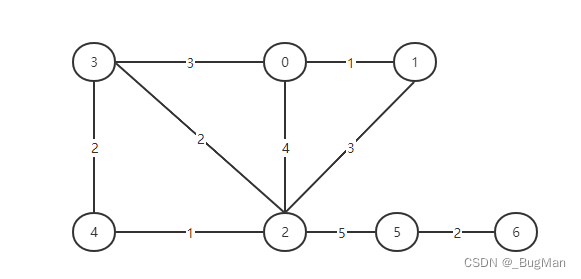
public class prim {
    static int[][] graph;
    static int[] dist;
    static int[] path=new int[7];
    static boolean[] isUsed=new boolean[7];
    static {
        graph=new int[][]{
                {0,1,4,3,0,0,0},
                {1,0,3,0,0,0,0},
                {4,3,0,2,1,5,0},
                {3,0,2,0,2,0,0},
                {0,0,1,2,0,0,0},
                {0,0,5,0,0,0,2},
                {0,0,0,0,0,2,0}
        };
        dist=new int[]{Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE};
    }
    public static void prim(){
        while(true){
            //判断节点是否已经全部纳入
            if(isOver()){
                break;
            }
            //寻找未纳入的节点中距离树最近的节点
            int i=findRecently();
            //设置为已遍历状态
            isUsed[i]=true;
            //遍历该节点邻接节点
            for (int j=0;j<graph[i].length;j++) {
                if(graph[i][j]!=0&&isUsed[j]==false){
                    //更新邻接节点的dist、path
                    flashDistAndPath(i,j);
                }
            }
        }
    }

    public static int findRecently(){
        int min=Integer.MAX_VALUE;
        int index=-1;
        for(int i=0;i<dist.length;i++){
            if(min>dist[i]&&isUsed[i]==false){
                min=dist[i];
                index=i;
            }
        }
        return index;
    }

    public static void flashDistAndPath(int i,int j){
        if (graph[i][j] < dist[j]) {
            dist[j] = graph[i][j];
            path[j] = i;
        }
    }

    public static boolean isOver(){
        int trues=0;
        for (boolean isused:isUsed) {
            if(isused==true){
                trues++;
            }
        }
        if(trues==dist.length){
            return true;
        }
        return false;
    }

    public static void main(String[] args) {
        isUsed[0]=true;
        dist[1]=1;
        path[1]=0;

        prim();
        for (int i=0;i<dist.length;i++){
            System.out.println(dist[i]);
        }
    }
}

13.3.kruskal算法

13.3.1.概述

kruskal算法，将森林合并成树，过程即使用贪心思想每次将不构成回路的最短边纳入。最后就是将一棵棵小树树组成的森林合成一课大树，即最小生成树。

为什么不构成回路喃，构成回路一定不会是最短路径，这个自行画图思考一下就能明白，或者参照下面例子也能理解。

以下图为例展示kruskal算法的全过程：

先将最小的边（权重为1）的纳入森林：

接下来将剩余最小的边（权重为2）纳入森林：

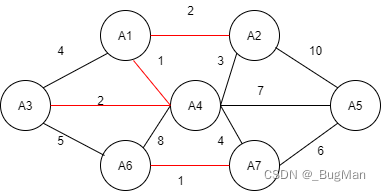
接下来将剩下最小的边（权重为4）纳入森林，不能纳入权重为3的边，因为纳入后会构成回路。有一条权重为4的边也因为纳入后会构成回路所以不能纳入森林：

这里就可以思考一下如果将构成回路的边纳入森林，会产生什么情况。

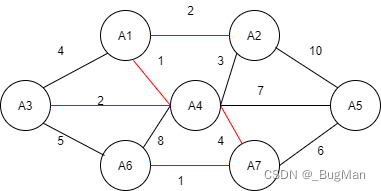
同理权重为5的边不能纳入，应该纳入权重为6的边，完成将每个节点纳入树，生成最小生成树：

13.3.2.代码实现

kruskal的实现偷个懒了，引用站内其他博主的实现：

原文链接：https://blog.csdn.net/weixin_48544279/article/details/126843851

（主要是当时想着kruskal的实现过程不复杂，就偷懒没留下自己的实现代码。哈哈哈~）

private int edgeNum; //边的个数
	private char[] vertexs; //顶点数组
	private int[][] matrix; //邻接矩阵
	//使用 INF 表示两个顶点不能连通
	private static final int INF = Integer.MAX_VALUE;

	public static void main(String[] args) {
		//创建顶点数组
		char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
		//图的邻接矩阵（二维数组）
		int matrix[][] = {
				        /*A*//*B*//*C*//*D*//*E*//*F*//*G*/
				/*A*/ {   0,  12, INF, INF, INF,  16,  14},
				/*B*/ {  12,   0,  10, INF, INF,   7, INF},
				/*C*/ { INF,  10,   0,   3,   5,   6, INF},
				/*D*/ { INF, INF,   3,   0,   4, INF, INF},
				/*E*/ { INF, INF,   5,   4,   0,   2,   8},
				/*F*/ {  16,   7,   6, INF,   2,   0,   9},
				/*G*/ {  14, INF, INF, INF,   8,   9,   0}};
		//大家可以在去测试其它的邻接矩阵，结果都可以得到最小生成树.

		//创建KruskalCase 对象实例
		KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
		
		kruskalCase.kruskal();
	}

	//构造器
	public KruskalCase(char[] vertexs, int[][] matrix) {
		//初始化顶点数和边的个数
		int vlen = vertexs.length;

		//初始化顶点, 复制拷贝的方式
		this.vertexs = new char[vlen];
		for(int i = 0; i < vertexs.length; i++) {
			this.vertexs[i] = vertexs[i];
		}

		//初始化边, 使用的是复制拷贝的方式
		this.matrix = new int[vlen][vlen];
		for(int i = 0; i < vlen; i++) {
			for(int j= 0; j < vlen; j++) {
				this.matrix[i][j] = matrix[i][j];
			}
		}
		//统计边的条数
		for(int i =0; i < vlen; i++) {
			for(int j = i+1; j < vlen; j++) {
				if(this.matrix[i][j] != INF) {
					edgeNum++;
				}
			}
		}

	}
	public void kruskal() {
		int index = 0; //表示最后结果数组的索引
		//用于保存"已有最小生成树" 中的每个顶点在最小生成树中的终点
		//用来判断是否出现回路
		int[] ends = new int[edgeNum];
		//创建结果数组, 保存最后的最小生成树
		EData[] rets = new EData[edgeNum];
		//统计最小生成树的总权值
		int totalWeight = 0;

		//获取图中 所有的边的集合 ， 一共有12边
		EData[] edges = getEdges();
		System.out.println("图的边的集合=" + Arrays.toString(edges) + " 共"+ edges.length); //12

		//按照边的权值大小进行排序(从小到大)
		sortEdges(edges);

		//遍历edges 数组，将边添加到最小生成树中时，判断是准备加入的边否形成了回路，如果没有，就加入 rets, 否则不能加入
		for(int i=0; i < edgeNum; i++) {
			//获取到第i条边的第一个顶点(起点)
			int p1 = getPosition(edges[i].start);
			//获取到第i条边的第2个顶点
			int p2 = getPosition(edges[i].end);

			//获取p1这个顶点在已有最小生成树中的终点
			int m = getEnd(ends, p1);
			//获取p2这个顶点在已有最小生成树中的终点
			int n = getEnd(ends, p2);
			//是否构成回路
			if(m != n) { //没有构成回路
				ends[m] = n; // 设置m 在"已有最小生成树"中的终点
				rets[index++] = edges[i]; //有一条边加入到rets数组
			}
		}
		//<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
		//统计并打印 "最小生成树", 输出  rets
		System.out.println("最小生成树为");
		for(int i = 0; i < index; i++) {
			System.out.println(rets[i]);
			totalWeight += rets[i].weight;
		}
		System.out.println("最小生成树的权值为：" + totalWeight);
	}
	/**
	 * 功能：对边进行排序处理, 冒泡排序
	 * @param edges 边的集合
	 */
	private void sortEdges(EData[] edges) {
		for(int i = 0; i < edges.length - 1; i++) {
			for(int j = 0; j < edges.length - 1 - i; j++) {
				if(edges[j].weight > edges[j+1].weight) {//交换
					EData tmp = edges[j];
					edges[j] = edges[j+1];
					edges[j+1] = tmp;
				}
			}
		}
	}
	/**
	 *
	 * @param ch 顶点的值，比如'A','B'
	 * @return 返回ch顶点对应的下标，如果找不到，返回-1
	 */
	private int getPosition(char ch) {
		for(int i = 0; i < vertexs.length; i++) {
			if(vertexs[i] == ch) {//找到
				return i;
			}
		}
		//找不到,返回-1
		return -1;
	}
	/**
	 * 功能: 获取图中边，放到EData[] 数组中，后面我们需要遍历该数组
	 * 是通过matrix 邻接矩阵来获取
	 * EData[] 形式 [['A','B', 12], ['B','F',7], .....]
	 * @return
	 */
	private EData[] getEdges() {
		int index = 0;
		//创建edges数组保存图的边
		EData[] edges = new EData[edgeNum];
		for(int i = 0; i < vertexs.length; i++) {
			//本来j应该从i开始遍历，但是顶点自身的邻接矩阵的位置为0
			for(int j=i+1; j <vertexs.length; j++) {//把自身为0的情况也排除，所以j = i + 1开始
				if(matrix[i][j] != INF) {  //不是无穷大，说明i j 两个顶点之间有边
					//把边加入到edges数组中
					edges[index++] = new EData(vertexs[i], vertexs[j], matrix[i][j]);
				}
			}
		}
		return edges;
	}
	/**
	 * 功能: 获取下标为i的顶点的终点(), 用于后面判断两个顶点的终点是否相同
	 * @param ends ： 数组就是记录了各个顶点对应的终点是哪个,ends 数组是在遍历过程中，逐步形成
	 * @param i : 表示传入的顶点对应的下标
	 * @return 返回的就是 下标为i的这个顶点对应的终点的下标, 一会回头还有来理解
	 */
	private int getEnd(int[] ends, int i) { // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
		while(ends[i] != 0) {
			i = ends[i];
		}
		return i;
	}

}

//创建一个类EData ，它的对象实例就表示一条边
class EData {
	char start; //边的一个点
	char end; //边的另外一个点
	int weight; //边的权值
	//构造器
	public EData(char start, char end, int weight) {
		this.start = start;
		this.end = end;
		this.weight = weight;
	}
	//重写toString, 便于输出边信息
	@Override
	public String toString() {
		return "边 <" + start + ", " + end + "> 权值为= " + weight + "";
	}
}