本节分析VIO初始化部分

VINS-Mono/Fusion代码学习系列：
从零学习VINS-Mono/Fusion源代码（一）：主函数
从零学习VINS-Mono/Fusion源代码（二）：前端图像跟踪
从零学习VINS-Mono/Fusion源代码（三）：IMU预积分公式推导
从零学习VINS-Mono/Fusion源代码（四）：误差卡尔曼滤波

1 为什么要做初始化？

提供初始值（良好的初始值，能够避免优化过程中系统陷入局部最小，减少迭代次数，降低计算量）

初始化的变量：
位姿、速度、零偏，硬件外参、地图点

其中，在没有先验条件的情况下，加速度计零偏和平移外参是比较难求解的，加计bias受到重力干扰，难以分离.
因此，平移外参一般是事先测量得到，加速度计零偏就设为0，在后续优化中进行处理.

2 初始化流程

estimator_node.cpp中找到主函数main()，主函数与光流部分类似，定义节点，设置参数，接收topic.

int main(int argc, char **argv)
{
    ros::init(argc, argv, "vins_estimator");
    ros::NodeHandle n("~");
    ros::console::set_logger_level(ROSCONSOLE_DEFAULT_NAME, ros::console::levels::Info);
    readParameters(n);
    estimator.setParameter();
#ifdef EIGEN_DONT_PARALLELIZE
    ROS_DEBUG("EIGEN_DONT_PARALLELIZE");
#endif
    ROS_WARN("waiting for image and imu...");

    registerPub(n);

    ros::Subscriber sub_imu = n.subscribe(IMU_TOPIC, 2000, imu_callback, ros::TransportHints().tcpNoDelay());
    ros::Subscriber sub_image = n.subscribe("/feature_tracker/feature", 2000, feature_callback);//前端光流结果
    ros::Subscriber sub_restart = n.subscribe("/feature_tracker/restart", 2000, restart_callback);//接收前端重启命令
    ros::Subscriber sub_relo_points = n.subscribe("/pose_graph/match_points", 2000, relocalization_callback);//回环检测fast_relocalization响应

    std::thread measurement_process{process};
    ros::spin();
 
    return 0;
}

2.1 参数读取

使用readParameters(n)读取yaml文件中估计器迭代计算参数、IMU参数、旋转平移外参，以及时间延迟参数.

estimator.setParameter() 估计器外参预设
本质上就是一个外参的赋值过程，然后设置特征点的置信度，默认在虚拟相机下，特征点投影后的坐标差为1.5个像素.

void Estimator::setParameter()
{
    for (int i = 0; i < NUM_OF_CAM; i++)
    {
        tic[i] = TIC[i];
        ric[i] = RIC[i];
    }
    f_manager.setRic(ric);

	//特征点置信度
    ProjectionFactor::sqrt_info = FOCAL_LENGTH / 1.5 * Matrix2d::Identity();
    ProjectionTdFactor::sqrt_info = FOCAL_LENGTH / 1.5 * Matrix2d::Identity();
    td = TD;
}

2.2 回调函数

IMU_callback()
IMU回调函数主要完成两个任务：

• 把imu消息存入buffer
• 根据IMU频率预测并发送位姿，提高里程计频率（对应系统框图propagation）

消息存入buffer的过程中用到了进程锁，避免数据放入和取出发生访问冲突，具体概念参见：
[c++11]多线程编程(六)——条件变量(Condition Variable)

void imu_callback(const sensor_msgs::ImuConstPtr &imu_msg)
{
    if (imu_msg->header.stamp.toSec() <= last_imu_t)
    {
        ROS_WARN("imu message in disorder!");
        return;
    }
    last_imu_t = imu_msg->header.stamp.toSec();

    m_buf.lock();
    imu_buf.push(imu_msg);
    m_buf.unlock();
    con.notify_one();

    last_imu_t = imu_msg->header.stamp.toSec();

    {
        std::lock_guard<std::mutex> lg(m_state);
        predict(imu_msg);
        std_msgs::Header header = imu_msg->header;
        header.frame_id = "world";
        if (estimator.solver_flag == Estimator::SolverFlag::NON_LINEAR)
            pubLatestOdometry(tmp_P, tmp_Q, tmp_V, header);
    }
}

feature_callback就是把前端光流数据丢进buffer
restart_callback做了一个状态器复位

2.3 Measurement_process{process} —— vio处理线程

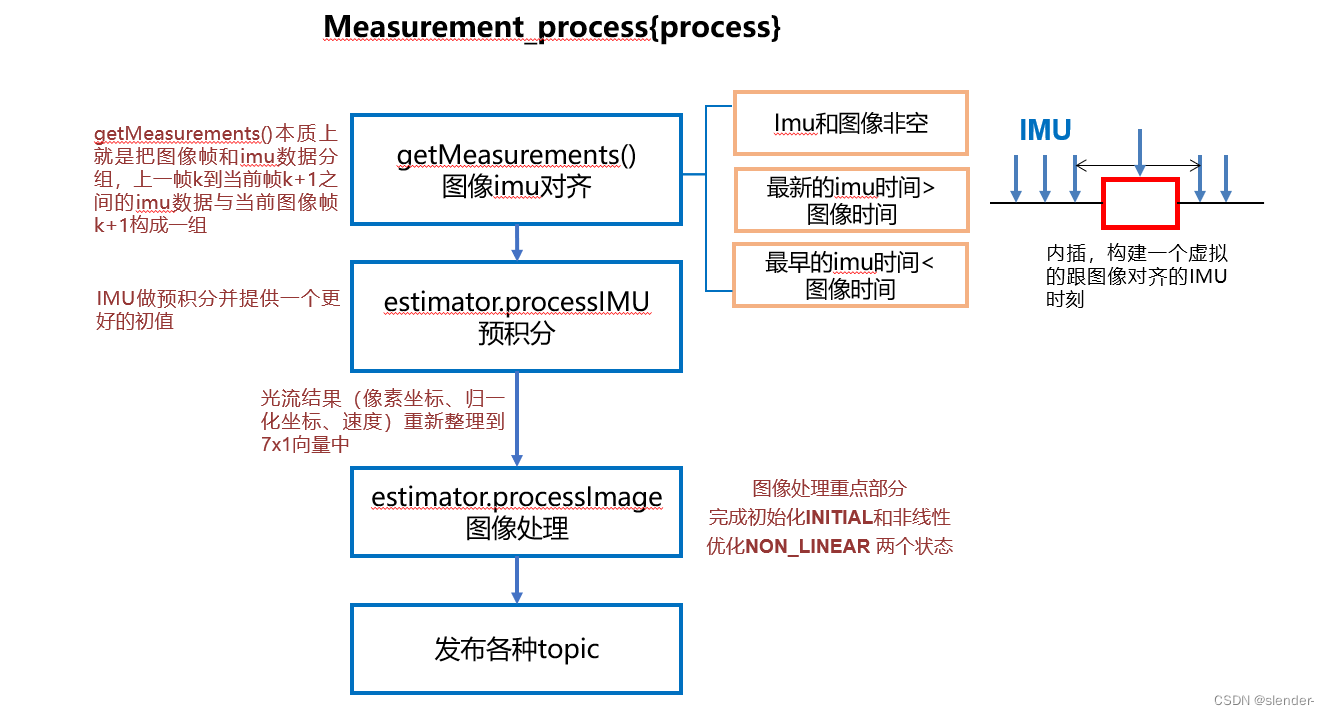
2.3.1 数据预处理

• getMeasurements()完成imu图像帧的时间同步(这个getMeasurements()，本质上就是把图像帧和imu数据分组，上一帧k到当前帧k+1之间的imu数据与当前图像帧k+1构成一组)；
• 之后，把imu送入estimator.processIMU做预积分，并且更新滑窗中的状态量Ps Vs Rs，给非线性优化提供更好的初值；
• 光流结果（像素坐标、归一化坐标、速度）重新整理到7x1向量xyz_uv_velocity中去.

2.3.2 VIO初始化任务

estimator.processImage函数中完成了VIO初始化和后端优化求解，本节只讨论VIO初始化任务：

1. 特征点管理，检查是否是关键帧 addFeatureCheckParallax
2. 旋转外参初始化 CalibrationExRotation
3. VIO初始化 initialStructure
   

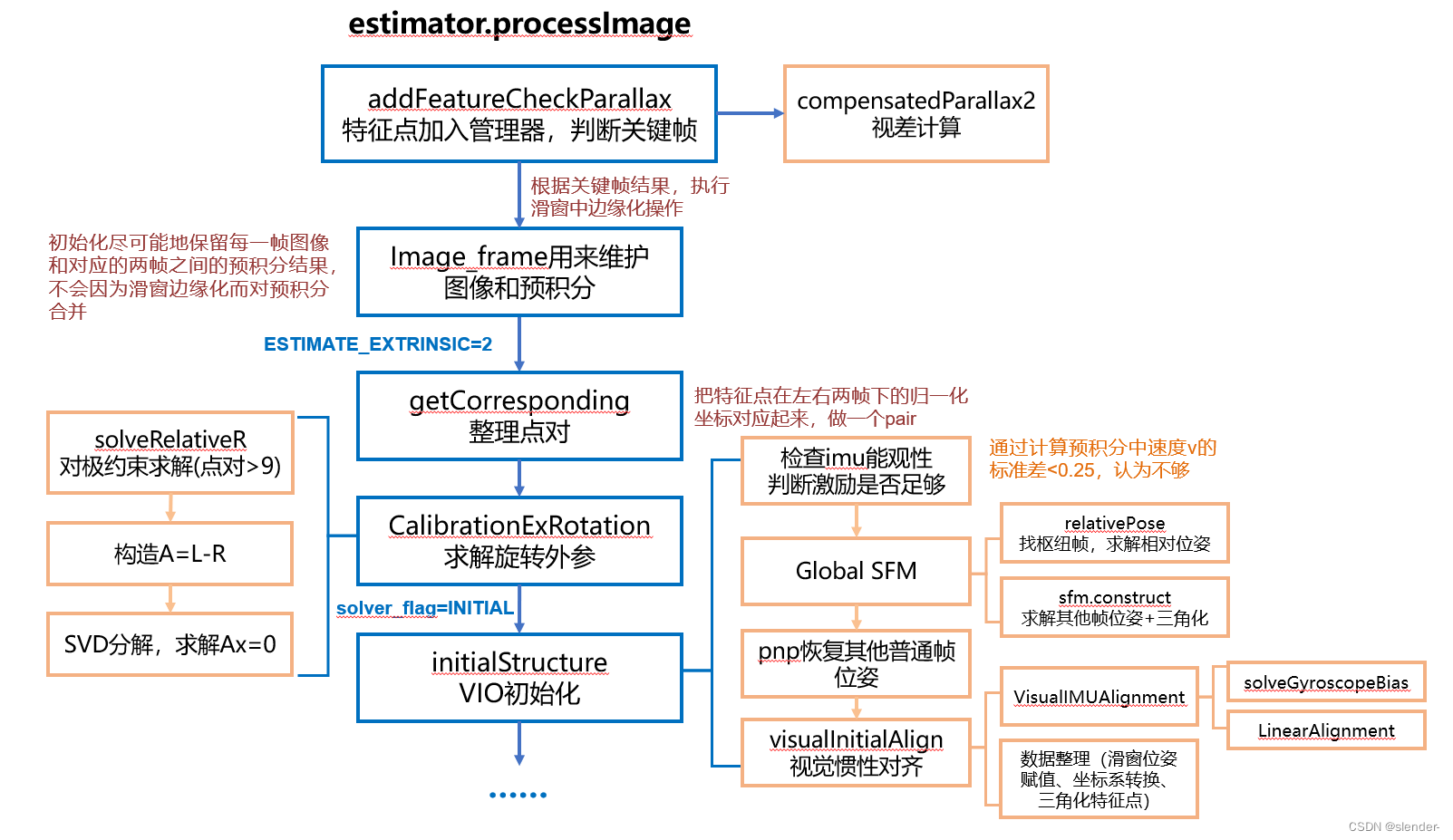
3 VIO初始化实现

3.1 特征点管理，检查是否是关键帧 addFeatureCheckParallax

把当前帧的特征点信息送入f_manager中进行维护，通过视差判断关键帧.

VINS特征点维护方式：
FeatureManager这个类中，有一项list< FeaturePerId > feature，用来维护下图中每一个特征点id对应的属性.

关键帧筛选条件：

• 是第0帧或第1帧（frame_count<2）
• 追踪到上一帧特征点数目少于20个（last_track_num<20）
• 计算倒数第二帧和倒数第三帧之间的视差（本质是判断倒数第二帧是不是关键帧）compensatedParallax2
• 与上一帧没有共视特征点（parallax_num==0）

如果倒数第二帧是关键帧，去掉最老帧；如果倒数第二帧不是关键帧，就把它去掉.

3.2 旋转外参初始化 CalibrationExRotation

只针对于 ESTIMATE_EXTRINSIC=2，才需要在初始化阶段计算旋转外参量.
思想就是利用k到k+n时刻中，各相邻两帧之间的旋转关系，构建超定方程求解.
这个旋转关系有两种途径得到：第一种是IMU预积分，第二种是特征点对极约束.

以k到k+1时刻为例，将外参$q_{cb}$作为桥梁，可以构建下面这个等式：

$q_{cb}\otimes q_{b_k{b}_{k+1}}=q_{c_k{c}_{k+1}}\otimes q_{cb}$
${\left[q_{b_k{b}_{k+1}}\right]}_R{q}_{cb}={\left[q_{c_k{c}_{k+1}}\right]}_L{q}_{cb}$

对于k到k+n时刻:

$\left(R_k-L_k\right)q_{cb}=0$
$\left(R_{k+1}-L_{k+1}\right)q_{cb}=0$
$⋮$
$\left(R_{k+n}-L_{k+n}\right)q_{cb}=0$

然后就构建了Ax=0这样的问题，通过SVD奇异值分解来求解.

3.3 VIO初始化 initialStructure

initialStructure函数中完成的任务：检查imu能观性、SFM纯视觉三维重建、对所有帧pnp、视觉惯性对齐

3.3.1 SFM部分

假设滑窗中有11帧，先找一个枢纽帧（假设第4帧），要求它离最后一帧尽可能远（目的是避免纯旋转情况，便于求解t），通过对极约束求解枢纽帧和最后一帧之间的相对位姿；同时，距离太远会导致两帧共同观测到的特征点数目少，所以要做一个权衡。

然后，根据得到的位姿，通过三角化恢复观测到的特征点的3D世界坐标.

利用已经恢复的3D点，通过pnp（3D-2D）来恢复第5-9帧的图像帧相对位姿，在这个过程中也可以三角化出更多的3D点.

同样地，利用pnp求解第3-0帧的图像帧位姿.

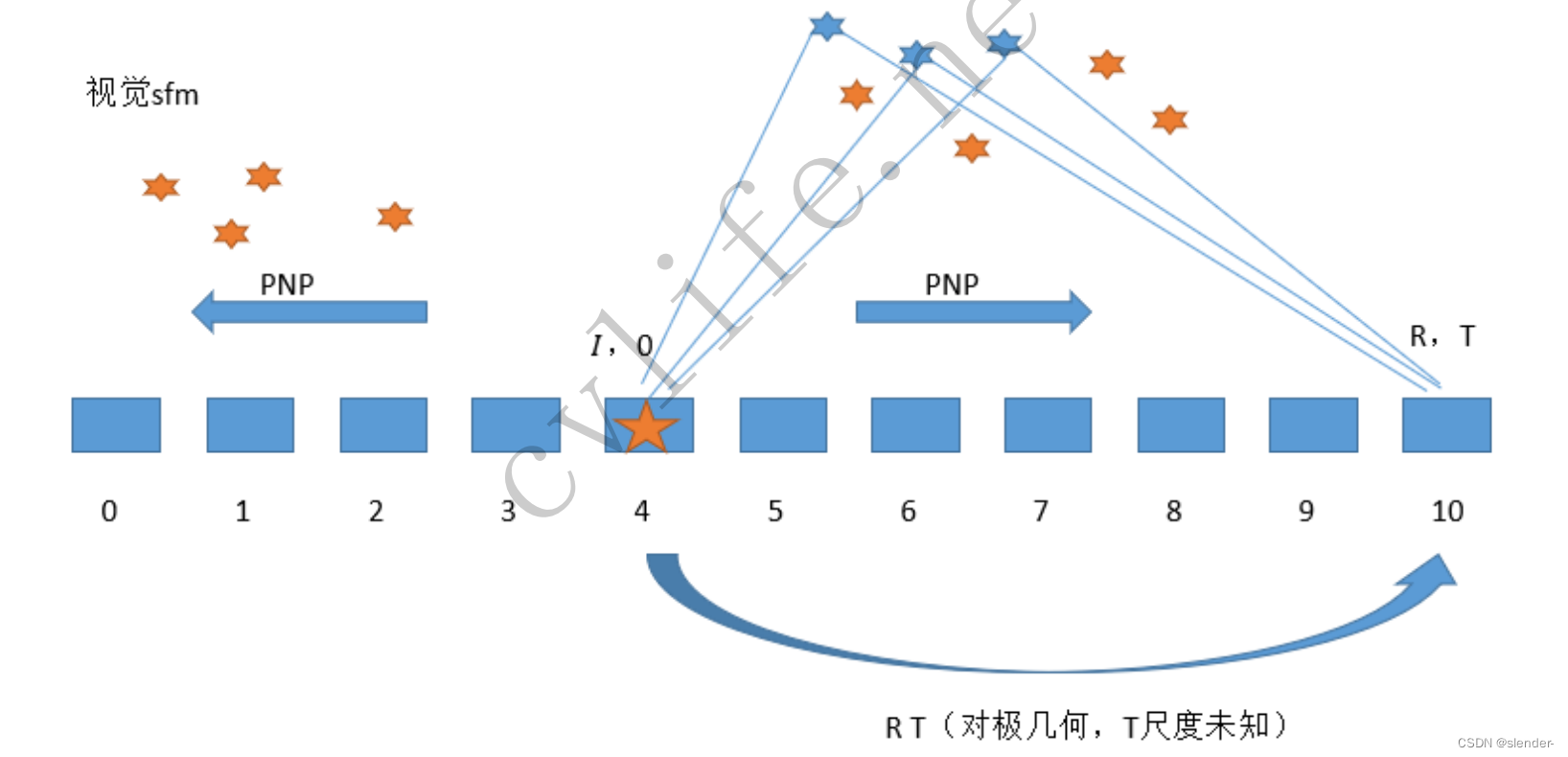
然后，做一个global BA，来调整这些位姿和3D点.

3.3.2 视觉惯性对齐

• solveGyroscopeBias求解陀螺零偏
  

  理论上为单位四元数，取出虚部构造Ax=b问题，求解$\delta b_w$：

• LinearAlignment求解速度、尺度、重力方向

  论文中指出的待求解量：
  
  构造的观测方程：
  
  推导一下这个方程怎么来的：
  首先把式（5）换到$c_0$系下面去（就是枢纽帧），然后带入式（14）.
  

  ①平移预积分量构成方程：

  $R_{c_0}^{b_k}{p}_{b_{k+1}}^{c_0}=R_{c_0}^{b_k}(p_{b_k}^{c_0}+v_{b_k}^{c_0}\Delta t_k-\frac{1}{2}{g}^{c_0}\Delta t_k^2)+\alpha$
  $R_{c_0}^{b_k}{p}_{b_{k+1}}^{c_0}=R_{c_0}^{b_k}(s{p}_{c_k}^{c_0}-R_{b_k}^{c_0}{p}_b^c+v_{b_k}^{c_0}\Delta t_k-\frac{1}{2}{g}^{c_0}\Delta t_k^2)+\alpha$
  $R_{c_0}^{b_k}(s{p}_{c_{k+1}}^{c_0}-R_{b_{k+1}}^{c_0}{p}_b^c)=R_{c_0}^{b_k}(s{p}_{c_k}^{c_0}-R_{b_k}^{c_0}{p}_b^c+v_{b_k}^{c_0}\Delta t_k-\frac{1}{2}{g}^{c_0}\Delta t_k^2)+\alpha$
  $\alpha -R_{c_0}^{b_k}{R}_{b_k}^{c_0}{p}_b^c+R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{p}_b^c=R_{c_0}^{b_k}(s{p}_{c_{k+1}}^{c_0}-s{p}_{c_k}^{c_0}-v_{b_k}^{c_0}\Delta t_k+\frac{1}{2}{g}^{c_0}\Delta t_k^2)$
  $\alpha -p_b^c+R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{p}_b^c=R_{c_0}^{b_k}(s{p}_{c_{k+1}}^{c_0}-s{p}_{c_k}^{c_0}-v_{b_k}^{c_0}\Delta t_k+\frac{1}{2}{g}^{c_0}\Delta t_k^2)$

  ②旋转预积分量构成方程：

  $R_{c_0}^{b_k}{v}_{b_{k+1}}^{c_0}=R_{c_0}^{b_k}(v_{b_k}^{c_0}-g^{c_0}\Delta t_k^{})+\beta$
  $R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{v}^{b_{k+1}}=R_{c_0}^{b_k}(R_{b_k}^{c_0}{v}^{b_k}-g^{c_0}\Delta t_k^{})+\beta$
  $\beta =R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{v}^{b_{k+1}}-v^{b_k}+R_{c_0}^{b_k}{g}^{c_0}\Delta t_k^{}$