前置基础

不同精度数据类型的动态范围

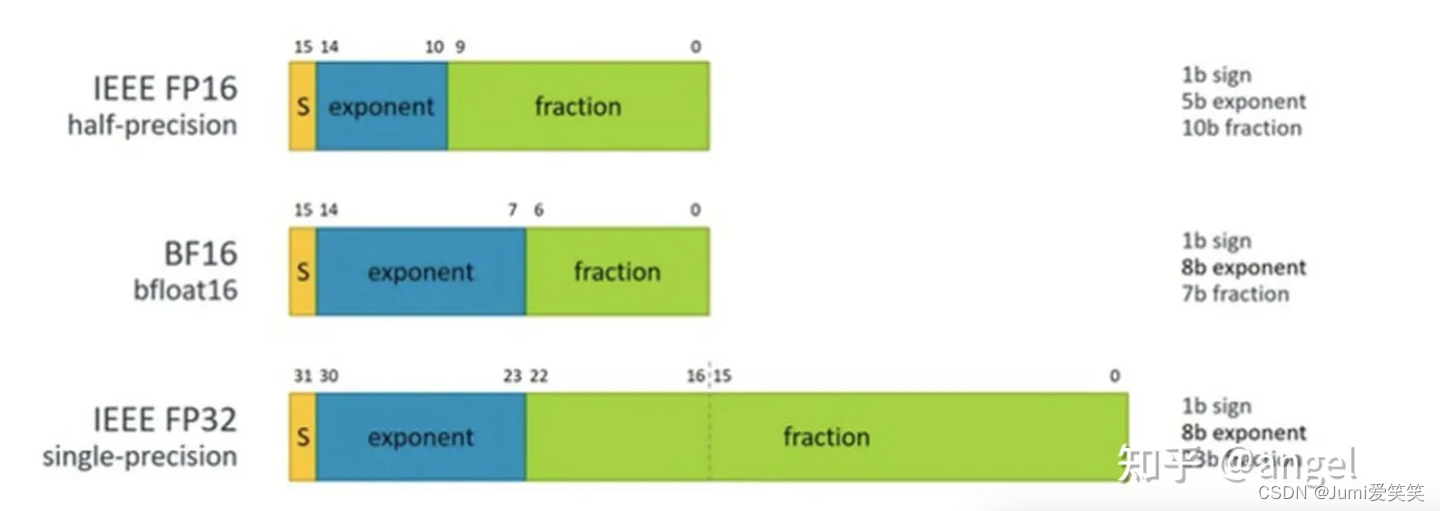
FP16的动态范围(6x10-8 ~ 65504)
FP32的动态范围(1.4x10-45 ~ 1.7x10+38)
可以看出Fp32的动态范围远大于fp16;
其中BF16的取值范围：
BF16（BFloat16）的取值范围也是按照IEEE 754标准定义的，它是一种16位浮点数格式，用于表示半精度浮点数。
BF16的取值范围为1个符号位（Sign Bit）、8个指数位（Exponent Bits）和7个尾数位（Significand Bits），总共16个位。符号位表示数的正负，指数位用于表示数的指数部分，尾数位用于表示数的尾数部分。这样就保留了FP32的近似动态范围；谷歌曾说过，这是因为神经网络对指数的大小比尾数敏感得多；
关于fp16的动态范围如何计算而来；
首先，看下十进制和二进制之间的转化：

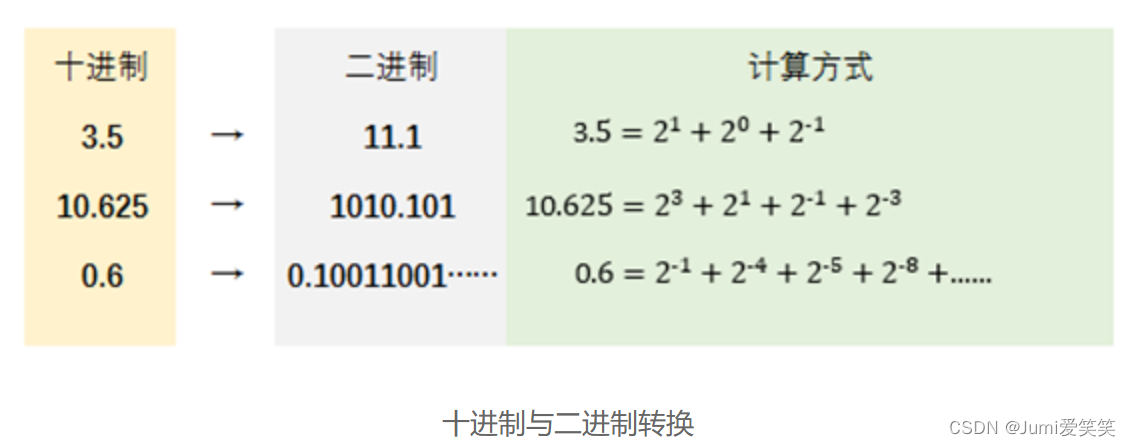
再看下二进制科学计数法的表达方式：

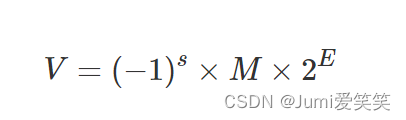
其中，s是符号位，M是尾数，E是阶数
frac的第一位隐含1：M = 1.xxx…x，由于小数点前默认是1，所以只用表示小数点之后的；
E是阶数；
对于FP16而言：

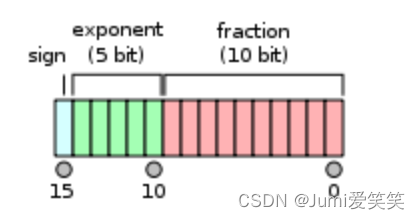
由于阶数有正有负，所以5位的exponent要抽一位出来表示正负~；还剩下四位，最多可以表示pow(2,4)-1=15,也就是阶数E最大可以到15，关于fraction部分是10位，最大可以是全11111111111，就是2^-1+2^-2+…+2^-10=0.999023
15*1.99903=65504;所以fp16最大的表示值就是65504
最小可以表达的非0正数是：
pow(2,-14)*pow(2,-10)=5.960464477539063e-08（非规格化表达方式，隐含进位）；

混合精度训练

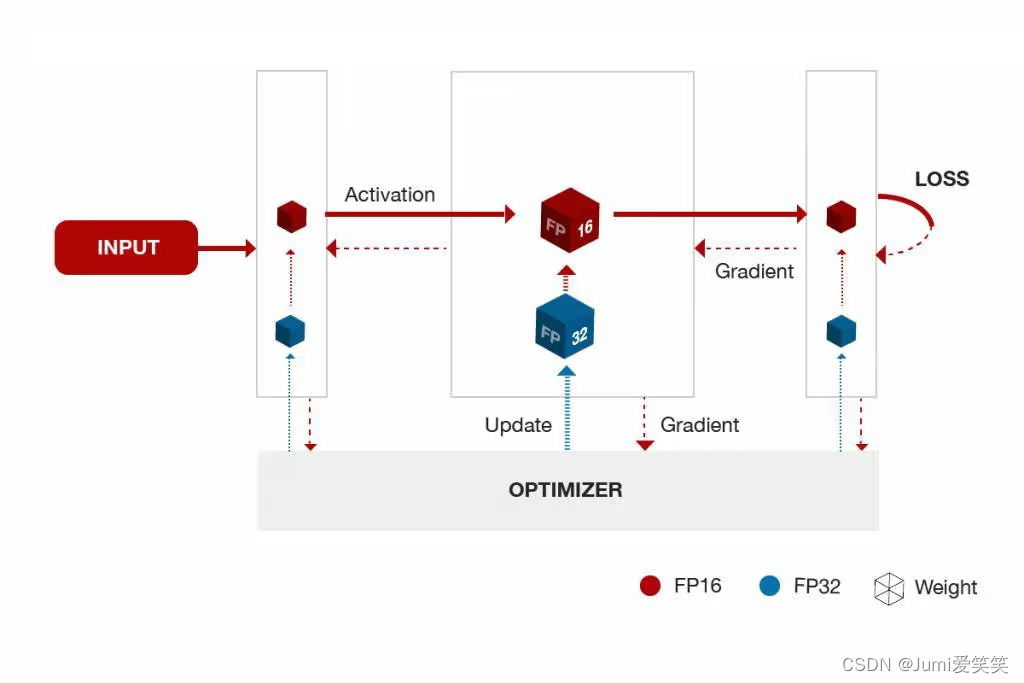
就是训练的时候前向推理用的是float16,然后优化的时候（就是计算梯度、更新参数的时候用的是float32);混合精度训练的好处就是可以节约内存、加速训练，同时可以保证精度；

反向传播
神经网络反向传播的过程可以看成是计算雅可比比矩阵连乘的过程；雅可比矩阵的连乘可以得到对某个参数的导数，根据该导数可以对该参数进行更新，关于具体的更新方式，不同的优化器有不同的方式；
所谓的雅可比矩阵就是y=f(x),其中y对于x的求导就是雅可比矩阵；

对于线性层，雅可比求导的结果就是权重；

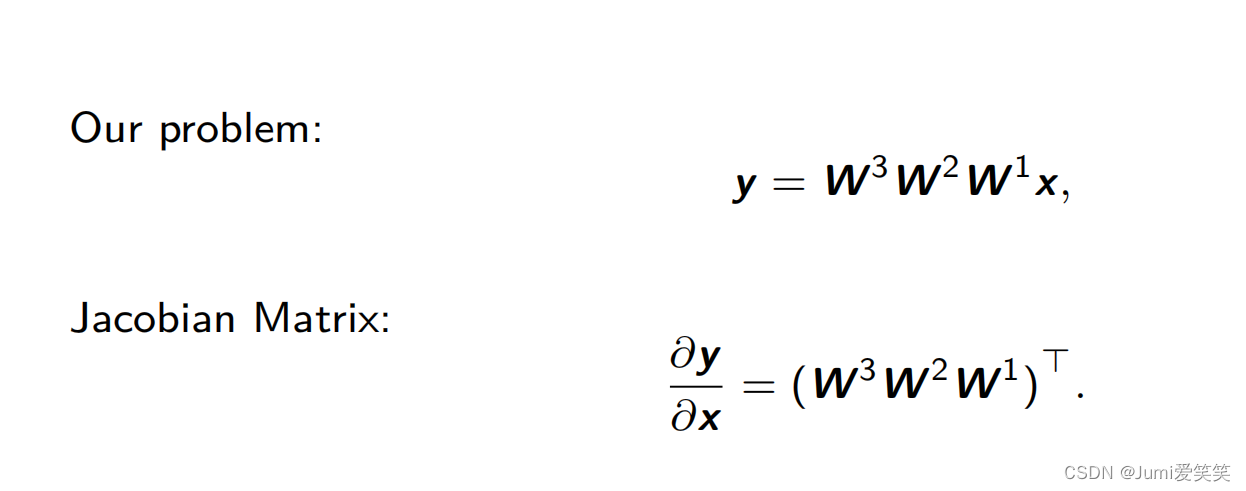
训练技巧

训练过程中，最容易出现梯度爆炸的层是LayNorm和self-attention,因为这两个层的梯度可能比较大，导致参数更新出现超过表达范围的异常值；
很少有激活层用y=x^2，原因在于梯度值可能会无穷大；

Lipschitz常量用来表征函数中斜率最大的值；
作者认为，斜率越大，代表参数的变化范围也就越大，也就代表越大的搜索空间，也就代表模型就更强的表达能力；但是也意味着训练会更加不稳定；所以在表达能力和训练稳定之间存在着一个trade off;

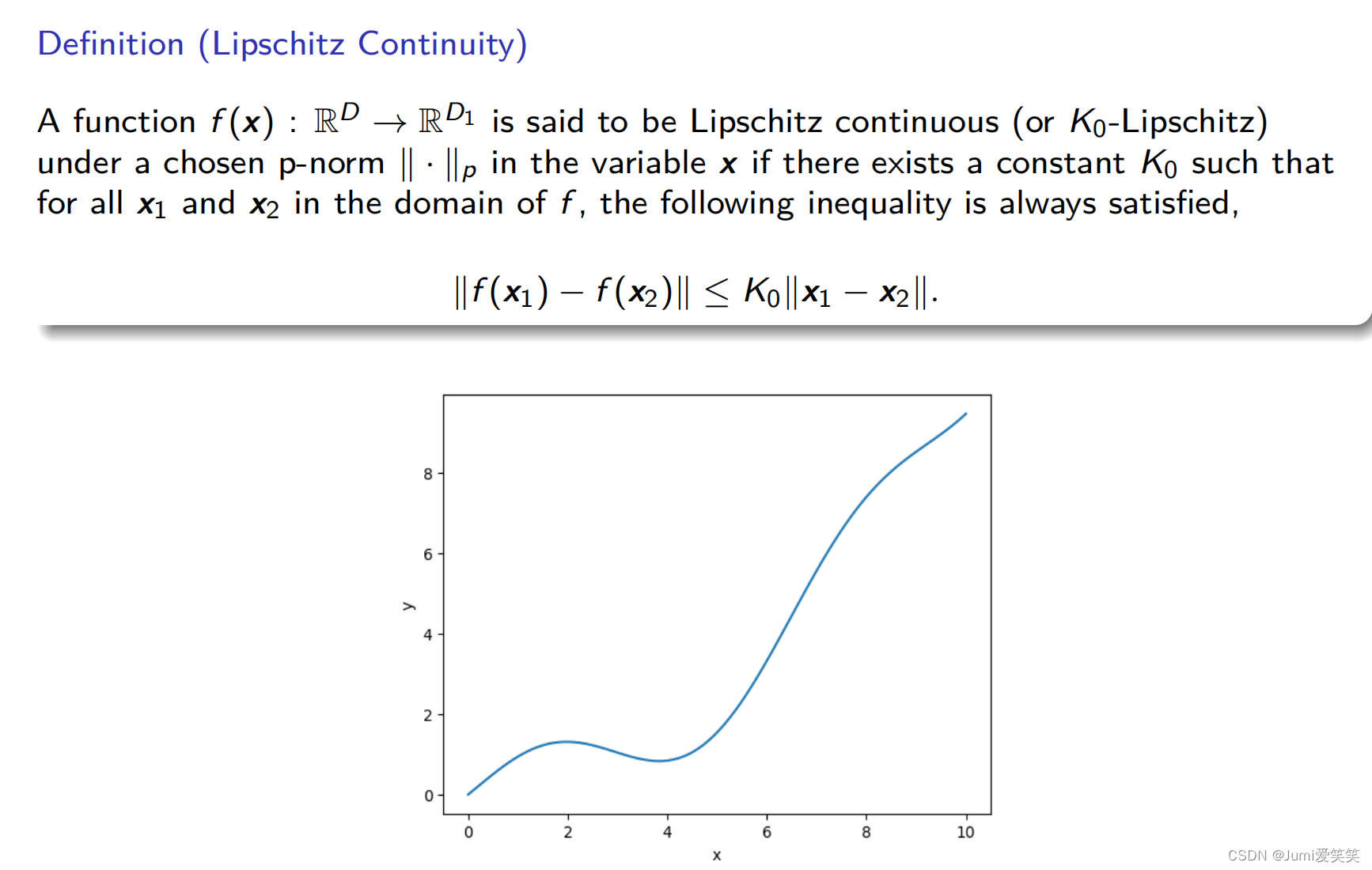
线性层和卷积层，本质上都是线性操作，卷积层相当于共享参数的线性操作，但是self-attention是高阶的非线性操作，ResNet是由齐次运算堆叠而成，关注局部区域，而transformer是由非齐次运算堆叠而成，关注更大区域和更高的语义，齐次和非齐次运算的雅可比矩阵有非常不同的特性，会导致不同的优化难度；

在实际工程训练过程中，我们都知道transformer的训练难度更大，对于更多参数量更复杂的模型，最好可以用大一点的weight_decay(weight_decay相当于对参数进行一定比例的缩放），需要更久的warm-up时长，需要更小的学习率，来防止梯度消失和梯度爆炸；SGD优化器可能会对一些比较小的网络（比如CNN)work,它用的是一阶导去进行参数更新，但是针对于复杂的大模型，需要用到Adam优化器会效果更好（因为adam用的是一个二阶导，且会对梯度进行缩放）；
但是以上的工程trick会缺乏理论的指导，

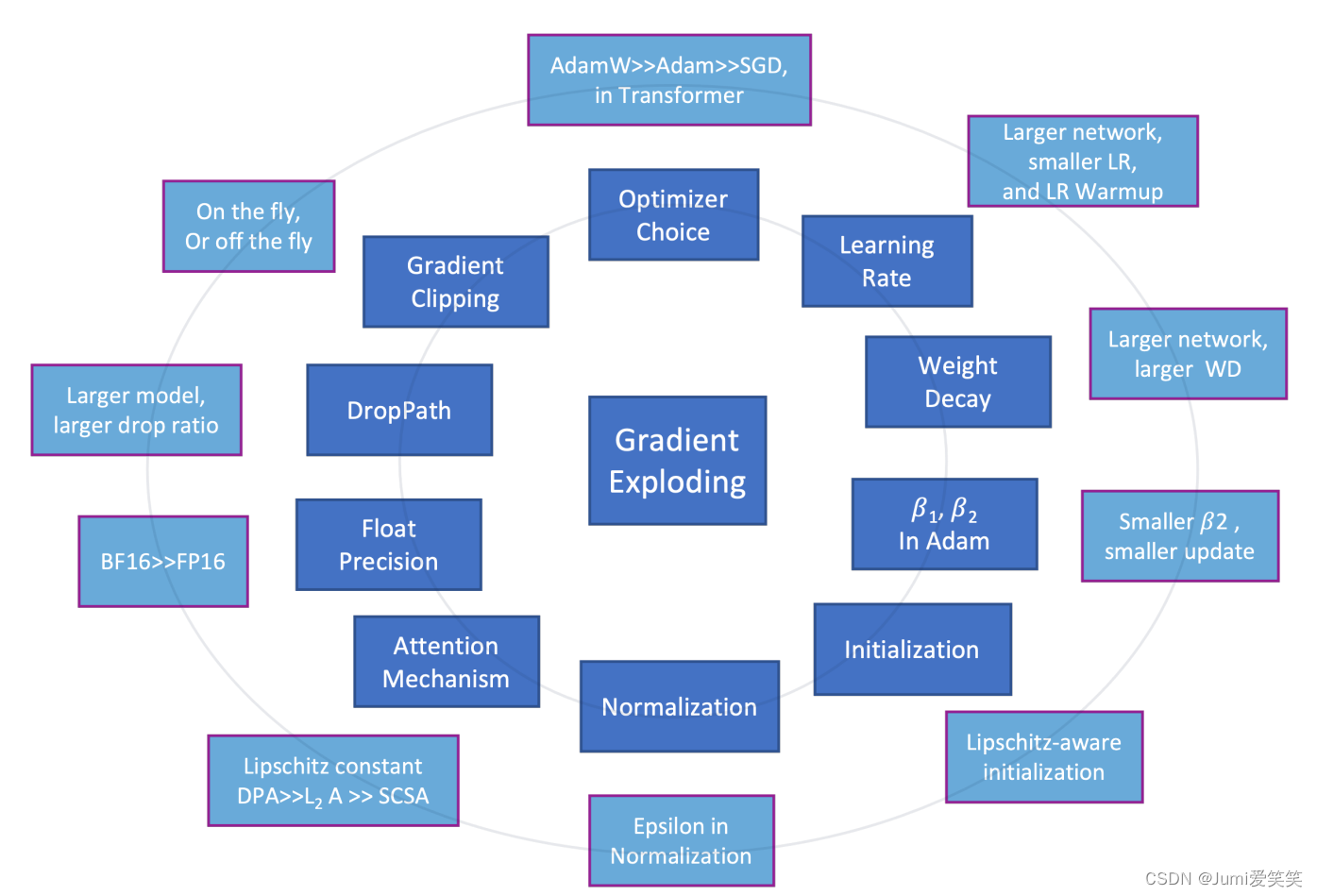
除开用clip或者scale的方式处理gradient或者weight,防止梯度爆炸以外，也要注意防止梯度消失，由于反向回传的原因，一般浅层的网络更容易发生梯度消失的问题；