前言
一、时间序列介绍
- 1-1、时间序列定义
- 1-2、时间序列特性
- 1-3、时间序列作用
二、统计学方法
- 2-1、移动平均法介绍
- - 2-1-1、基本原理、计算过程
  - 2-1-2、移动平均法分类
  - - 2-1-3、简单移动平均法
    - 2-1-4、加权移动平均法
    - 2-1-5、指数移动平均法（Exponential Moving Average，EMA）
    - 2-1-6、累积移动平均（Cumulative Moving Average，CMA）
    - 2-1-7、比较
总结

前言

时间序列（英语：time series）是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值（如1秒，5分钟，12小时，7天，1年），因此时间序列可以作为离散时间数据进行分析处理。时间序列广泛应用于数理统计、信号处理、模式识别、计量经济学、数学金融、天气预报、地震预测、脑电图、控制工程、航空学、通信工程以及绝大多数涉及到时间数据测量的应用科学与工程学。（来源：维基百科）

一、时间序列介绍

1-1、时间序列定义

时间序列：时间序列是按照时间顺序排列的一组数据点。这些数据点可以是在连续的时间点（例如每秒、每分钟、每小时）或者在固定的时间间隔（例如每天、每周、每月、每季度、每年）上观察到的。

1-2、时间序列特性

时间序列数据有一些特殊的特性，这些特性使得它们与其他类型的统计数据有所不同。以下是一些主要的特性：

时间依赖性：时间序列数据的一个关键特性是观察值之间的依赖性。这意味着一个时间点的数据可能会受到其历史数据的影响。例如，今天的股票价格可能会受到过去几天或几个月的股票价格的影响。
季节性：许多时间序列数据会显示出季节性的模式，这意味着在一年中的特定时间，数据会有一定的模式或趋势。例如，零售业的销售额通常在假日季节（如圣诞节）期间会有所增加。
趋势：趋势是指时间序列数据随着时间的推移呈现出的持续上升或下降的模式。例如，一个公司的年销售额可能会显示出持续增长的趋势。
周期性：周期性是指数据在固定的时间间隔内显示出的模式或波动。这不同于季节性，因为周期性的模式不一定与日历时间（如季节或月份）有关。例如，经济可能会经历几年的增长和衰退的周期。
不稳定性：许多时间序列数据可能会随着时间的推移而变得不稳定，这可能是由于市场条件的变化、政策的变化、技术的进步等因素引起的。

1-3、时间序列作用

时间序列分析在许多领域都有重要的应用，主要有以下几个作用：

预测：时间序列分析的一个主要应用是预测未来的数据点。通过理解过去的数据模式，我们可以预测未来的趋势、季节性模式等。例如，企业可能会使用时间序列分析来预测未来的销售额，以便更好地进行库存管理和资源规划。
异常检测：时间序列分析也可以用于检测数据中的异常值或者突变。例如，如果一个服务器的流量突然增加，这可能意味着服务器正在遭受攻击，或者有一些其他的问题。
理解底层模式和关系：时间序列分析可以帮助我们理解数据的底层模式和关系。例如，我们可以使用时间序列分析来理解经济周期，或者理解股票价格的波动。
政策或计划评估：时间序列分析也可以用于评估政策或计划的效果。例如，政府可能会使用时间序列分析来评估税收政策的影响，或者评估公共卫生干预的效果。
信号处理：在信号处理领域，时间序列分析可以用于提取有用的信号，或者消除噪声。

二、统计学方法

2-1、移动平均法介绍

2-1-1、基本原理、计算过程

移动平均法的基本原理：通过计算数据集中一段连续的数据点的平均值，以平滑数据并揭示出数据的潜在趋势或周期性模式。这种方法特别适用于时间序列数据，因为它可以帮助我们消除短期的波动，以便更好地理解数据的长期趋势。移动平均法的关键概念是“移动窗口”。这个窗口定义了我们要计算平均值的数据点的数量。例如，如果我们有一组每日销售数据，我们可以选择一个7天的窗口，这意味着我们每次计算的是最近7天的平均销售额。

移动平均法的计算过程如下：

选择一个窗口大小。这个窗口大小决定了我们要考虑的数据点的数量。
对于每一个时间点，计算其在窗口内的所有数据点的平均值。这个平均值就是该时间点的移动平均值。
将窗口向前移动一步，然后重复第2步，直到计算出所有时间点的移动平均值。

2-1-2、移动平均法分类

移动平均法是一种常用的时间序列分析方法，主要用于平滑数据以揭示潜在的趋势或周期性模式。根据计算方式的不同，移动平均法主要可以分为以下几种：

简单移动平均（Simple Moving Average，SMA）：这是最基本的移动平均法，它计算的是每个窗口内的数据的平均值。例如，一个7天的简单移动平均就是过去7天数据的平均值。
加权移动平均（Weighted Moving Average，WMA）：在加权移动平均中，每个数据点都有一个权重，这个权重决定了该数据点在平均值中的重要性。通常，最近的数据会被赋予更大的权重，因为它们更能反映当前的情况。
指数移动平均（Exponential Moving Average，EMA）：指数移动平均是一种特殊的加权移动平均，它给每个数据点赋予的权重会随着时间的推移而指数衰减。这意味着最近的数据会被赋予最大的权重，而越早的数据权重越小。
累积移动平均（Cumulative Moving Average，CMA）：累积移动平均是从数据开始到当前点的所有数据的平均值。这种方法的特点是每个新的数据点都会影响到所有的平均值。

这些移动平均法各有优缺点，适用于不同的情况。简单移动平均易于理解和计算，但可能会忽略最近的数据变化。加权移动平均和指数移动平均可以更好地反映最近的数据变化，但计算起来更复杂。累积移动平均则可以反映长期的趋势，但可能会受到早期数据的影响。

2-1-3、简单移动平均法

简单移动平均法（Simple Moving Average，SMA）：是一种常用的时间序列分析方法，用于平滑数据并识别趋势。它通过计算一系列连续数据点的平均值来生成预测值，从而减少数据的波动性，更好地展现长期趋势。

简单移动平均的计算方法很简单：对于给定的时间序列数据，选择一个固定大小的窗口（如n个数据点），然后计算窗口内数据点的平均值作为预测值。随着时间的推移，窗口向前滑动，并且每次都会重新计算平均值。这样，我们就可以得到一系列平滑后的预测值，用于分析趋势和周期性。

下面是一个使用Python实现简单移动平均的示例代码：

import numpy as np
import matplotlib.pyplot as plt

def simple_moving_average(data, window_size):
    weights = np.repeat(1.0, window_size) / window_size
    sma = np.convolve(data, weights, 'valid')
    return sma

# 原始数据
data = np.array([3, 5, 7, 6, 9, 8, 7, 6, 7, 8, 10, 12])

# 移动平均窗口大小
window_size = 3

# 计算简单移动平均
sma = simple_moving_average(data, window_size)

# 绘制原图形
plt.plot(data, label='Original')
# 绘制经过移动平均的图形
plt.plot(range(window_size-1, len(data)), sma, label='SMA')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()

输出：
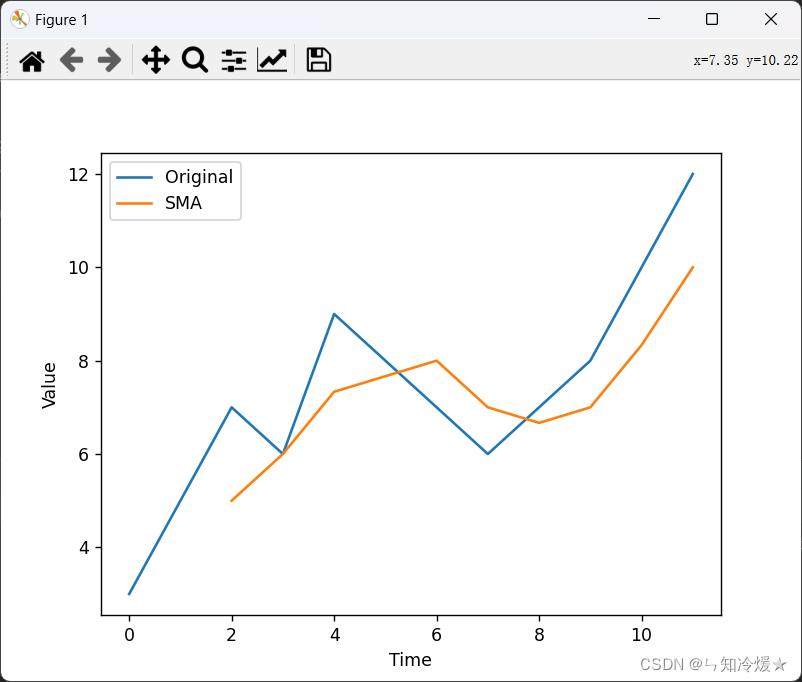
在这里插入图片描述

结论：通过使用简单移动平均法，我们可以对时间序列数据进行平滑处理，并更好地观察长期趋势。请注意，窗口大小的选择会影响到平滑程度和响应速度，较小的窗口大小可以更敏感地反映近期变化，而较大的窗口大小则更适用于分析长期趋势。

2-1-4、加权移动平均法

加权移动平均法（Weighted Moving Average，WMA）：是一种基于权重分配的时间序列分析方法，与简单移动平均法相比，加权移动平均法对不同时间点的数据赋予不同的权重，以更好地反映不同时间点对预测值的影响。

加权移动平均的计算方法如下：对于给定的时间序列数据，选择一个固定大小的窗口（如n个数据点），并为窗口内的每个数据点分配一个权重。通常，较新的数据点具有较高的权重，较旧的数据点具有较低的权重。然后，按照权重的比例计算加权平均值作为预测值。随着时间的推移，窗口向前滑动，并重新计算加权平均值。

下面是一个使用Python实现加权移动平均的示例代码，并绘制原图形和经过加权移动平均后的图形：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体为中文宋体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

def weighted_moving_average(data, weights):
    """
    计算加权移动平均

    参数：
    data: 时间序列数据（一维数组）
    weights: 权重（一维数组，与数据点对应）

    返回值：
    移动平均结果（一维数组）
    """
    ma = np.convolve(data, weights, mode='valid')
    return ma


# 示例数据
data = [10, 12, 15, 14, 16, 18, 17, 19, 20, 22]
weights = [0.1, 0.2, 0.3, 0.4]

# 计算加权移动平均
wma = weighted_moving_average(data, weights)

# 绘制原图形
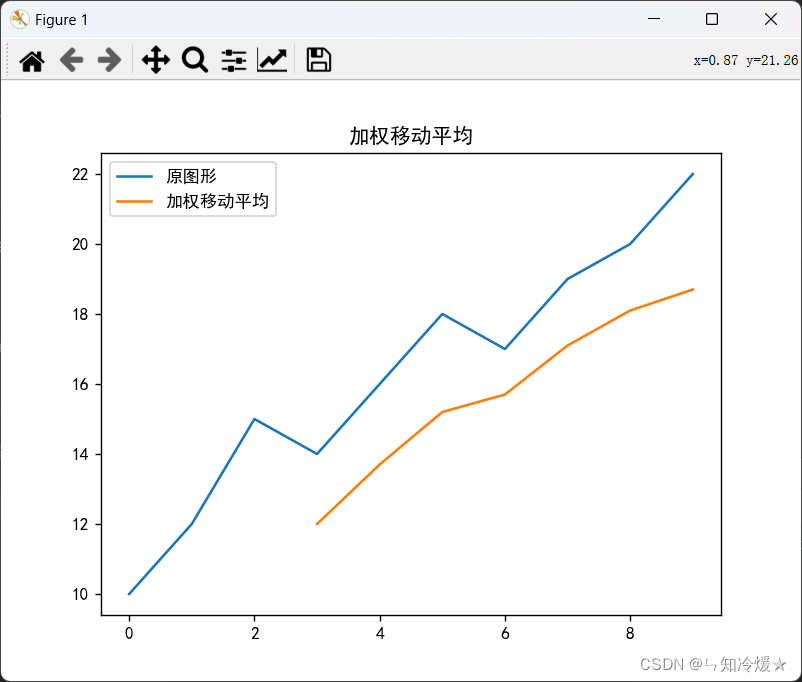
plt.plot(data, label='原图形')

# 绘制加权移动平均后的图形
plt.plot(range(len(weights) - 1, len(data)), wma, label='加权移动平均')

# 添加图例和标题
plt.legend()
plt.title('加权移动平均')

# 显示图形
plt.show()

输出如下所示：
在这里插入图片描述

2-1-5、指数移动平均法（Exponential Moving Average，EMA）

指数移动平均法（Exponential Moving Average，EMA）：是一种常用的时间序列分析方法，用于平滑数据并捕捉趋势的变化。与简单移动平均法和加权移动平均法不同，指数移动平均法赋予最近数据点更高的权重，较旧的数据点权重逐渐减小，以更好地反映近期数据对预测值的影响。

指数移动平均的计算方法如下：对于给定的时间序列数据，选择一个平滑系数（一般记为α），通常取值范围在0到1之间。然后，根据以下公式计算指数移动平均值：

$EM A (t) = α * d a t a (t) + (1 - α) * EM A (t - 1)$

其中，EMA(t)表示当前时刻的指数移动平均值，data(t)表示当前时刻的原始数据，EMA(t-1)表示上一时刻的指数移动平均值。通过不断更新指数移动平均值，可以得到一系列平滑后的预测值。

下面是一个使用Python实现指数移动平均的示例代码，并绘制原图形和经过指数移动平均后的图形：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体为中文宋体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题


def exponential_moving_average(data, alpha):
    """
    计算指数移动平均

    参数：
    data: 时间序列数据（一维数组）
    alpha: 平滑系数

    返回值：
    移动平均结果（一维数组）
    """
    ema = [data[0]]
    for i in range(1, len(data)):
        ema.append(alpha * data[i] + (1 - alpha) * ema[i - 1])
    return ema


# 示例数据
data = [10, 12, 15, 14, 16, 18, 17, 19, 20, 22]
alpha = 0.3

# 计算指数移动平均
ema = exponential_moving_average(data, alpha)

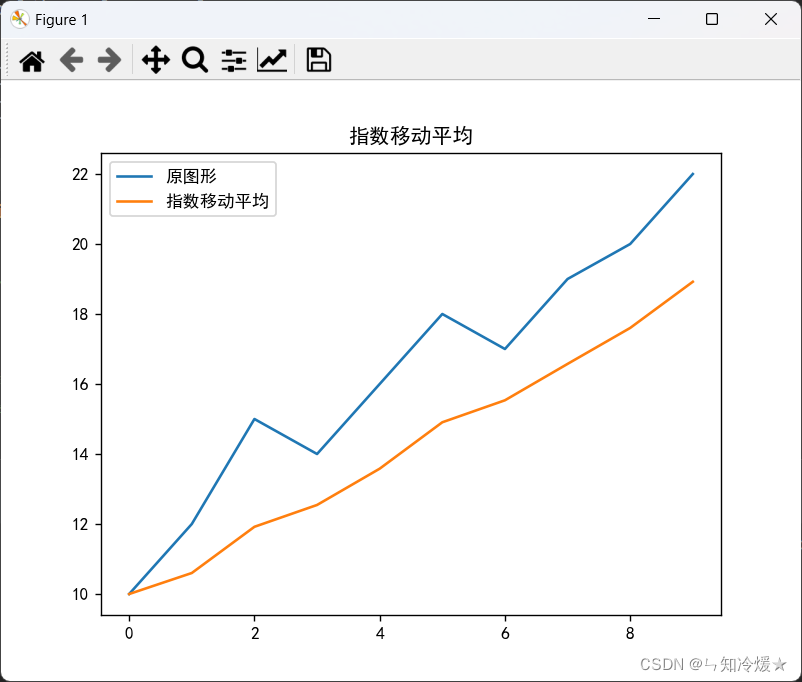
# 绘制原图形
plt.plot(data, label='原图形')

# 绘制指数移动平均后的图形
plt.plot(range(len(data)), ema, label='指数移动平均')

# 添加图例和标题
plt.legend()
plt.title('指数移动平均')

# 显示图形
plt.show()

输出：
在这里插入图片描述

2-1-6、累积移动平均（Cumulative Moving Average，CMA）

累积移动平均（Cumulative Moving Average，CMA）：是一种用于平滑时间序列数据的方法，它是一种累积式的平均方法。与简单移动平均和加权移动平均不同，累积移动平均不需要指定固定的窗口大小，而是将所有之前的数据都纳入平均计算中。

累积移动平均的计算方法如下：对于给定的时间序列数据，首先初始化一个累计计数器和一个累计和。然后，对于每个数据点，依次进行累计计算。具体步骤如下：

1、初始化累计计数器count为0和累计和cumulative_sum为0。
2、对于每个数据点data[i]，执行以下操作：

将累计计数器count加1。
将累计和cumulative_sum加上当前数据点data[i]。
计算累积移动平均值cma为累计和cumulative_sum除以累计计数器count。
将当前的累积移动平均值cma存储到结果列表中。

通过不断累计计算累积移动平均值，可以得到一系列平滑后的预测值。

下面是一个使用Python实现累积移动平均的示例代码，并绘制原图形和经过累积移动平均后的图形：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体为中文宋体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

def cumulative_moving_average(data):
    """
    计算累积移动平均

    参数：
    data: 时间序列数据（一维数组）

    返回值：
    移动平均结果（一维数组）
    """
    cma = []
    cumulative_sum = 0

    for i in range(len(data)):
        cumulative_sum += data[i]
        cma.append(cumulative_sum / (i + 1))

    return cma


# 示例数据
data = [10, 12, 15, 14, 16, 18, 17, 19, 20, 22]

# 计算累积移动平均
cma = cumulative_moving_average(data)

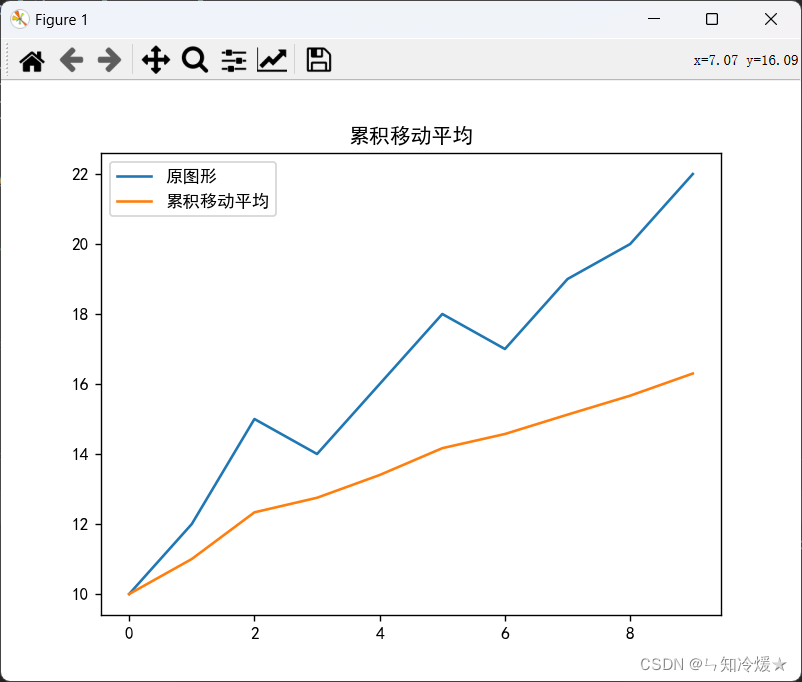
# 绘制原图形
plt.plot(data, label='原图形')

# 绘制累积移动平均后的图形
plt.plot(range(len(data)), cma, label='累积移动平均')

# 添加图例和标题
plt.legend()
plt.title('累积移动平均')

# 显示图形
plt.show()