[目录]
- 0. 前言
- 1. 简单随机
- 2. 可用位置内随机
- 3. 二叉树权重随机
- (1)分区域随机
- (2)设置权重均衡概率
- (3)二叉树缓存权重
- (4)利用二叉树随机
- (5)优缺点
- 4. 测试对比
- 4. 结束咯
0. 前言
在做个小游戏,需要随机在网格的空位置上生成方块,在随机的时候,感觉简单随机的方式效率很低而且不稳定。就在想有没有比较快的方式能够随机到想要的位置。最后是用二叉树记录下权重并进行随机,很稳定而且效率还不错。所以写个文章记录一下,以供参考。
1. 简单随机
在一个固定的网格中随机一个空位置。比如说在一个20*20的棋盘上,上面有若干个棋子,现在要生成新的棋子在空的位置上。最简单的方式就是在矩形内随机一个坐标,然后判断该位置是否有棋子,没有的话再随机一次,如下。
public Vector2Int RandomPos()
{
int x, y;
do
{
x = Random.Range(0, bound.width);
y = Random.Range(0, bound.height);
}
while (flagMap[x, y]);
return new Vector2Int(x, y);
}
这样简单随机容易在空位比较少的时候随机很久才能随机到空位,比如只剩下一个位置,那20*20的格子,就是1/400的概率随机到,那就需要重复很多次了。而且有安全问题,比如现在棋子都下满了没位置生成时调用就会无限循环。
稍微改进方法的是,加一个外额随机次数限制,比如说最多随机个1000次,如果没有,就当没有空位。解决死循环、随机太多次的问题,会跟推荐一点。总的来说:
优点:编写简单,运行较快,特别是地图大,空位多的时候随机非常快。
缺点:空位少时,运行时间长,容易漏掉某个位置随机不到,不稳定
2. 可用位置内随机
除了直接随机坐标的方式,还有另一种简单方法,就是预先计算一下可用位置,然后在可用位置内随机。
public Vector2Int RandomPos()
{
int w = flagMap.GetLength(0);
int h = flagMap.GetLength(1);
// 计算所有可能
tempPos.Clear();
for (int i = 0; i < w; i++)
{
for (int j = 0; j < h; j++)
{
if (!flagMap[i, j])
{
tempPos.Add(new Vector2Int(i, j));
}
}
}
// 随机一个
if (tempPos.Count <= 0)
{
return Vector2Int.zero;
}
else
{
int index = Random.Range(0, tempPos.Count);
return tempPos[index];
}
}
这种方法就是非常稳定,如果有空位毕竟可以随机到,而且不会有脸黑多次随机的问题。带来的额外问题就是,计算并记录所有位置需要额外的开销。
稍微改进方法是,在放置或者移除棋子的时候预先保存可用位置计数n,[0,n)之间随机出m,然后再依次找到第m个空位,即为随机位置。这样就可以减少检查和缓存的数据量。那么,这种方法的话:
优点:稳定,不会遗漏空位。地图小的时候,而且对空位要求严格的时候还是挺好用的。
缺点:效率低,特别是地图大的话,要计算一下所有的位置就比较麻烦了。
3. 二叉树权重随机
终于到了今天要讲的这个方法了,是按照分区域随机的思路想出来的。
(1)分区域随机
比如说我们可以先将网格分成均分成4个部分,然后随机一个位置,这个小区域也可以再划分为4个区域,直到剩下4个位置,就可以在这4个位置中随机一个,如果没有空位了。则重新跳回上一层区域再随机其他位置,如此重复。如下图(8*8)可供参考。
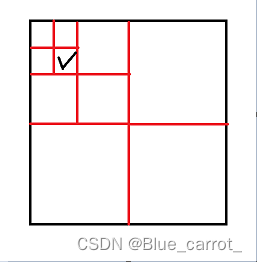
分层的最主要目的还是为了,在保证能够随机出空位的前提下,减少每次计算的量,不用每次都将地图从头开始判断是否可用。
(2)设置权重均衡概率
那么这个时候,聪明的小伙子就会发现这个方法的问题,概率不随机。比如说,如下图(4*4),我们在随机到左上区域的概率是1/4,但里面只有两个空位,那么这个时候这两个空位就会享受这1/8的概率。而右下的4空位分别只有1/16的概率。
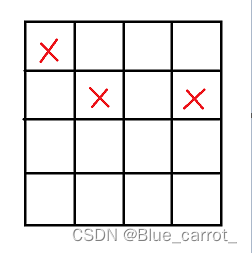
解决问题的方法,是计算并缓存一下权重,比如说左上只有两个空位,随机时享有2的权重,右下享有4的权重。如何比较好的计算并保存这个权重呢?刚刚随机区域的时候,有没有感觉很像深度优先搜索。这也让我联想到树结构,就打算用二叉树来做这个权重的缓存,而且二叉树有个好处就是非此即彼,每次只要判断一下做或者右即可。
(3)二叉树缓存权重
我们先考虑将这个数组降到1维,因为一维的话就只有左右之分, 更符合二叉树。我们编个号,可以随机的位置权重为1,不可以随机的位置权重为0。如下图。
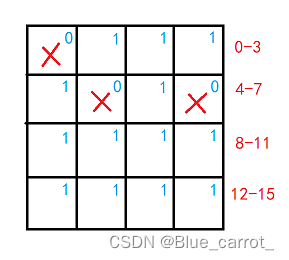
那么我们就就可以得到如下的二叉树,蓝色为权重。
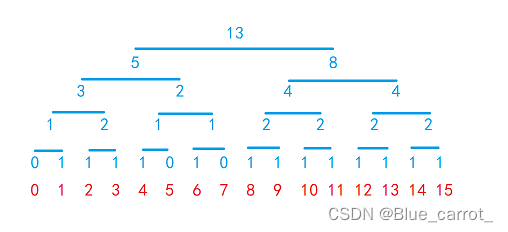
这种情况下,需要缓存的数据也不会太多,毕竟是取对数的,越往上消减得越快,缓存的数据在格子数量的2倍以内。而且为了存储和索引更加简单,我们用可以数组(记为weight)存一下这个二叉树。刚刚举的例子是一个16格的网格,意外(故意)刚好是2的指数倍,如果是3*3共9格,那就需要把后面的10-15权重置零就可以了。
另外是修改权重也会比较简单,每次放置或者移除棋子时,往上更改权重即可,如下。
public void SetEnable(int x, int y, bool enable)
{
int index = Pos2Index(x, y);
if (index < 0 &&
index >= weight[layerCount - 1].Length)
{
throw new System.Exception("x,y is out of Length");
}
int value = enable ? 1 : 0;
SetWeight(index, value);
}
private void SetWeight(int index, int value)
{
int changeValue = value - weight[layerCount - 1][index];
if (changeValue != 0)
{
for (int layer = layerCount - 1; layer >= 0; layer--)
{
weight[layer][index] += changeValue;
index = index >> 1; // =index /2;
index = index > 0 ? index : 0;
}
}
}
private int Pos2Index(int x, int y)
{
int i = x - gridBound.x;
int j = y - gridBound.y;
return i * gridBound.height + j;
}
其中,SetEnable 用于设置改位置是否可以被随机到,SetWeight 用于设置权重,Pos2Index用于转换坐标到一维数组的坐标。
(4)利用二叉树随机
随机的时候。首先是[0,13)内随机一个数,假设是9好了,大于或等于5,所以可以判断是右边部分。对于下一个节点判断是,9 - 5=4,大于或等于4,所以是判断为左边。依次不断进行到网格最底部就可以了,还是挺好理解的。那么代码如下。
public Vector2Int RandomPos()
{
if (IsEmpty)
{
return Vector2Int.zero;
}
else
{
int index = 0;
int value = Random.Range(0, weight[0][0]);
for (int layer = 1; layer < layerCount; layer++)
{
if (value >= weight[layer][index])
{
value -= weight[layer][index];
index = (index << 1) + 1;// i*2+1
}
else
{
index = index << 1;
}
}
return Index2Pos(index);
}
}
好咯,那么到现在,我们就可以又快又稳定的随机到这个点了。
(5)优缺点
优点:随机稳定,效率高。如果有空位一定能够随机到
缺点:额外内存开销,设置可否随机状态时有额外计算开销。
不适合地图比较大的情况,不过通常要严格随机位置的,应该不会区域太大,围棋棋盘也就19*19,看起来也挺密密麻麻的了。
4. 测试对比
简单测试一下,这个【3.二叉树权重随机】,和【1. 简单随机】比较一下。
在20*20的大小内,有一半已经有棋子的情况下,随机200次的时间开销。
RectInt rect = new RectInt(0, 0, 20, 20);
int repeatTime = 1000;
int setPosCount = 200;
int randomCount = 200;
RandomGrid grid = new RandomGrid(rect);
for (int j = 0; j < setPosCount; j++)
{
Vector2Int pos = grid.RandomPos();
grid.SetEnable(pos, false);
}
long time = System.DateTime.Now.Ticks;
for (int i = 0; i < repeatTime; i++)
{
for (int j = 0; j < randomCount; j++)
{
grid.RandomPos();
}
}
DebugU.Log("time1:" + (System.DateTime.Now.Ticks - time));
RandomGrid2 grid2 = new RandomGrid2(rect);
for (int j = 0; j < setPosCount; j++)
{
Vector2Int pos = grid2.RandomPos();
grid2.SetEnable(pos, false);
}
time = System.DateTime.Now.Ticks;
for (int i = 0; i < repeatTime; i++)
{
for (int j = 0; j < randomCount; j++)
{
grid2.RandomPos();
}
}
DebugU.Log("time2:" + (System.DateTime.Now.Ticks - time));
time1:179407
time2:259427
time1为二叉树权重随机的时间,time1比time2要快挺多,说明二叉树权重随机的方法效率还不错的,下面是网格内有不同数空位情况下,两种花费时间。
// 380个空位 / 95% 为空位
time1:149498
time2:89699
// 300个空位 / 75% 为空位
time1:179401
time2:149499
// 200个空位 / 50% 为空位
time1:179407
time2:259427
// 100个空位 / 25% 为空位
time1:129564
time2:358803
// 20个空位 / 5% 为空位
time1:129571
time2:2178037
比较一下,也可以发现二叉树权重随机会更加稳定一点,而且效率也还不错。其实最重要的是能够确保,有空位的时候能够随机到该位置。
4. 结束咯
在实际用二叉树权重随机的方法的时候,有个问题,比如我想要随机出一个3*3的小空位,而不是单独一个点,那么这个时候就没办法直接随机了。另外,比如需要限定点在第一第二行内,这种带范围的随机,也不好处理。
那么这个时候,我是用了一个临时权重TempWeight,原本的权重Weight,需要加上这个值才是最后的权重值。那么在随机的点不是3*3的空位(或者其他条件)时,在该位置TempWeight置为-1,那么和Weight相加为0,即权重为0,不会再随机到。然后我们再重复操作,直到找到符合要求的点。完成之后就可以重置一下TempWeight,不会影响下次操作。当然,如果下次随机的条件也是相同的,那还是可以先暂时保留TempWeight,以提高随机小卢。
ok,那就结束咯。
突发奇想的一个方法,希望能够各位有所帮助。