他们力量的源泉,是值得信赖的搭档以及想要保护的对象还有强大的敌人
本文收录于青花雾气-计算机基础
往期回顾
从汇编代码探究函数栈帧的创建和销毁的底层原理
从0到1搞定在线OJ
数据在内存中的存储
计算机存储的大小端模式
目录
浮点数的二进制转化及存储规则等
浮点数计算规则
1.指数向高位对齐
2.运算过程中的进位问题
大家好,我是纪宁。
这篇博客将给大家介绍浮点数在内存中是如何进行计算的
浮点数的二进制转化及存储规则等
在上次介绍了数据在内存中是如何存储的,其中就介绍了浮点数是如何在内存中存储的
不懂浮点数的二进制是如何转化和存储的可以去看我的这篇博客
数据在内存中的存储
其中详细介绍了浮点数的二进制如何转化以及国际标准IEEE规定的浮点数在内存中的存储方法
以下为简单复习
一个浮点数可以统一写成 (-1)^S * M * 2^E,其中(-1)^S表示这个浮点数的正负,当S=0时,表示这个浮点数为正值;S=1表示这个浮点数为负值。M表示有效数字,大于等于1,小于2,上例中有效数字M就是1.01101。2^E表示指数位,上例中E=2。如图所示
以5.625举例子,5.625的二进制位形式是101.101
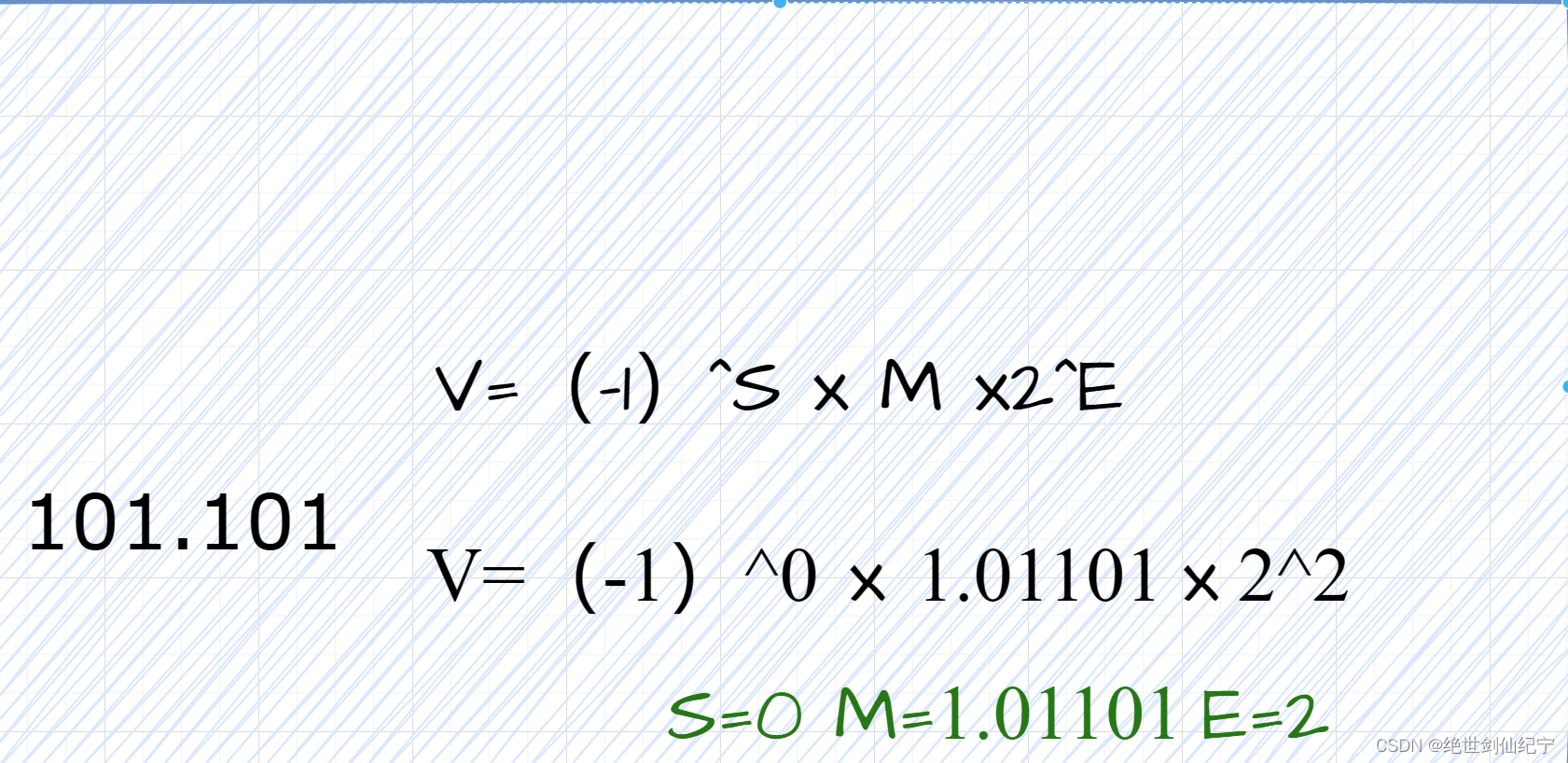
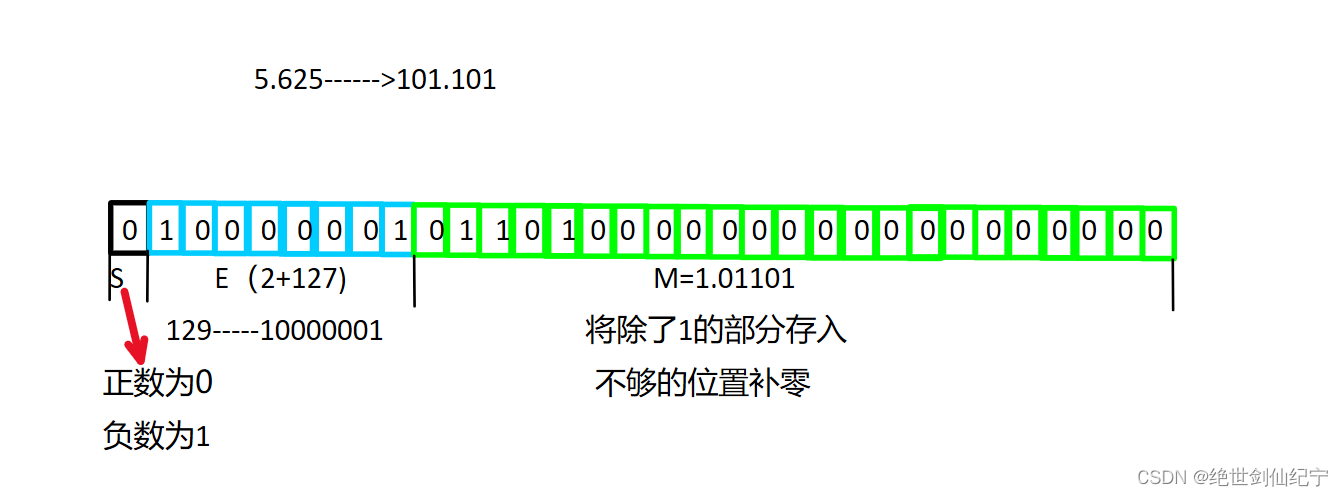
这是浮点数在内存中的存储形式
E+127/255存入,M去掉1存入
说了这么多,但是浮点数在内存中到底是如何计算的呢?
其实浮点数计算和存储的时候还是略有差别
浮点数计算规则
1.指数向高位对齐
什么意思呢?
如果两个浮点数进行相加,一个的E=3,一个的E=2,那么就要将E=2的浮点数转化为E=3的浮点数
转化方法就是改变这个浮点数的有效数字,将有效数字再次前移
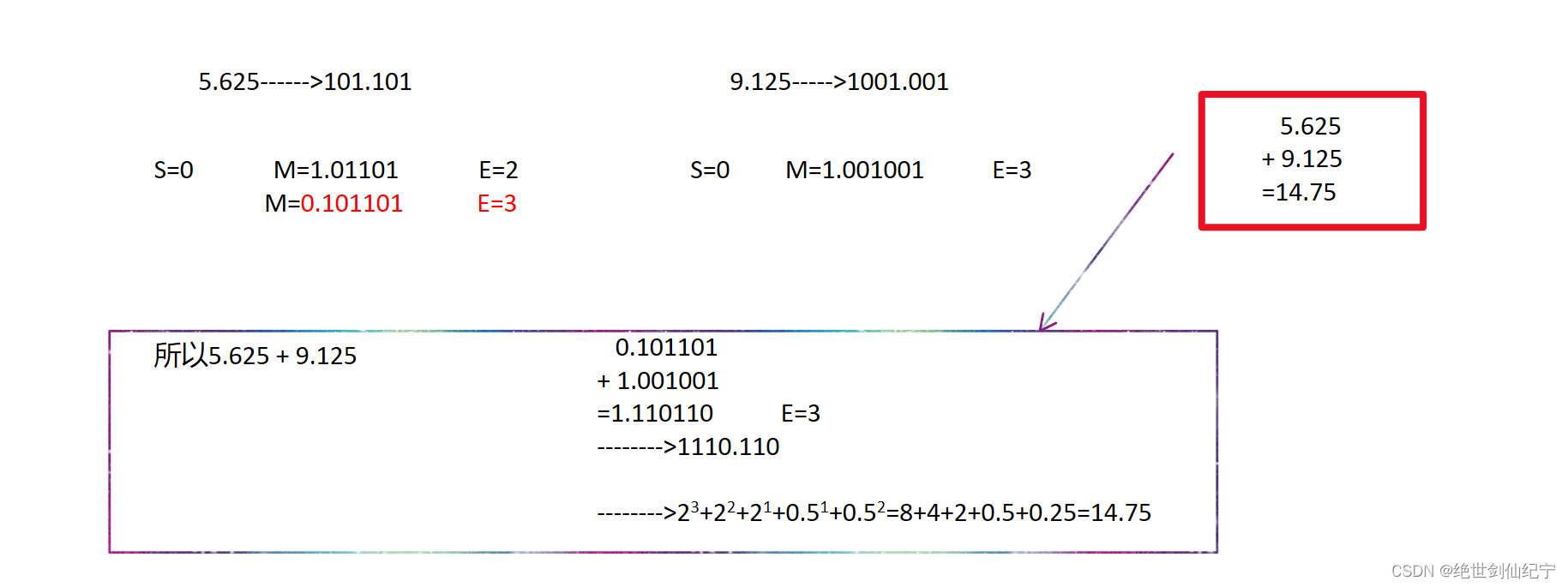
例如5.625要与9.125相加
5,625的E=2,有效数字为1.01101
9.125的E=3,有效数字为1.001001
5.625的E小于9.125的E,所以将5.625的E改为3,同时将它的有效数字前移1位
从1.01101变成0.101101
所以在计算的时候,5.625的V就变了,如图
将改变之后的M部分按二进制位运算方法运算,这个结果就是最终结果的有效数字
再将这个数字乘指数部分即可以得到最终结果
2.运算过程中的进位问题
上例解释了5.625和9.125的相加,但他们有效数字的小数点后第一位的数字加起来没有超过1,那么该如何计算呢?计算完又将如何存储?
例如进行5.625+9.75的浮点数运算
9.75----->1001.11----->1.00111 E=3

可以看出,当出现进位的情况,在计算的时候正常计算即可,只需要存储的时候有所差别
因为计算M结果的时候并不是在存储位置本身的地方进行的,是先取出来计算,然后计算完将结果重新储存进去,所以不用担心会有溢出的情况
内存有足够的空间去存储
那么浮点数在内存中的运算到这里就结束了,因为计算机CPU中只有加法
至于浮点数的乘法、减法、除法等,都可以转化为浮点数的‘加法’
如一个浮点数减一个浮点数
可以转化为一个浮点数加另一个浮点数的负数,其他都是类似的原理