1 知识点讲解

1.1 线性回归

线性回归是一种常见的机器学习算法，用于预测连续型变量。该算法的目标是建立一个线性模型，根据输入的自变量来预测一个连续型的因变量。

在线性回归中，我们假设因变量（也称为响应变量）与自变量之间存在线性关系。这意味着我们可以使用一条直线来拟合数据，并使用这条直线来进行预测。线性回归可以用于单个自变量或多个自变量的情况。

线性回归的目标是通过最小化预测值与实际值之间的差异来确定最佳拟合直线的参数。这个差异通常被称为残差，我们使用最小二乘法来计算残差和拟合直线的参数。最小二乘法可以使得残差的平方和最小，从而得到最佳的拟合直线。

最小二乘法是一种常用的线性回归算法，用于确定最佳拟合直线的参数。它的目标是通过最小化预测值与实际值之间的差异来确定最佳拟合直线的参数。

设有 $n$ 个样本，每个样本都有一个自变量 $x_i$ 和一个因变量 $y_i$。我们假设因变量 $y_i$ 与自变量 $x_i$ 之间存在线性关系，即

$$y_i={\beta }_0+{\beta }_1{x}_i+{ϵ}_i$$
其中 ${\beta }_0$ 和 ${\beta }_1$ 是我们要求解的拟合直线的参数，${ϵ}_i$ 是模型中的误差项。我们的目标是找到最佳的 ${\beta }_0$ 和 ${\beta }_1$，使得预测值与实际值之间的差异最小。

最小二乘法的基本思想是最小化残差平方和，即

$$\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$
其中 $\widehat{y_i}$ 表示用拟合直线预测的值，可以表示为

$$\widehat{y_i}={\beta }_0+{\beta }_1{x}_i$$
我们要求解的是使得残差平方和最小的 ${\beta }_0$ 和 ${\beta }_1$。为了求解这个问题，我们需要对残差平方和进行求导，并令导数等于零。这样就可以得最小化残差平方和的解，即

$${\beta }_1=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}$$

$${\beta }_0=\bar{y}-{\beta }_1\bar{x}$$

其中，$\bar{x}$ 和 $\bar{y}$ 分别为自变量和因变量的平均值。

这些公式可以用矩阵形式表示为：

$$\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\end{array}\right]=(X^{T}X{)}^{-1}{X}^{T}Y$$

其中，X 是一个nX2的矩阵，第一列为 1，第二列为自变量 $；Y 是 nX1 的矩阵，表示因变量 y。

1.2 多元线性回归及评估

1.2.1 多元线性回归模型

多元线性回归是一种用于分析多个自变量和一个因变量之间关系的线性回归模型。它可以用于预测因变量的值，给定多个自变量的值。多元线性回归的模型可以表示为：
$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_n{x}_n+ϵ$$
其中，$y$ 是因变量，$x_1,x_2,\cdots ,x_n$ 是 $n$ 个自变量，${\beta }_0,{\beta }_1,{\beta }_2,\cdots ,{\beta }_n$ 是模型的系数，$ϵ$ 是误差项。

多元线性回归的目标是找到最佳的系数 ${\beta }_0,{\beta }_1,{\beta }_2,\cdots ,{\beta }_n$，使得模型预测值与真实值之间的平方误差最小。这个过程通常使用最小二乘法进行求解。

1.2.2 评估

涉及总离差平方和的分解为回归平方和+残差平方和，这部分知识可根据需要查阅，

• 拟合优度R^2（判定系数、决定系数、样本可决系数）

$$R^2=1-\frac{{\sum }_{i=1}^n(y_i-\widehat{y_i}{)}^2}{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}$$

范围：0到1（闭区间）

越接近1，说明样本回归线对样本值的拟合优度约好，X对Y的解释能力越强。

Adj.R-square：Adj为adjust的缩写，代表调整之后的决定系数。对模型复杂度进行了惩罚，以更准确地评估模型的预测能力。
$$Adj.R^2=1-\frac{(1-R^2)(n-1)}{n-p-1}$$
其中，$n$ 是样本数量，$p$ 是自变量数量。Adj. $R^2$ 具有以下特点：

1. 当模型中的自变量数量增加时，Adj. $R^2$ 的值会减小，因为增加自变量会增加模型的复杂度，需要对其进行惩罚。

2. 当模型中的自变量数量为1时，Adj. $R^2$ 和 $R^2$ 的值相等。

3. 和 $R^2$ 一样，Adj. $R^2$ 的取值范围为 $[0,1]$，其值越接近1，表示模型对数据的拟合越好。

Adj. $R^2$ 是一种常用的模型评估指标，在多元线性回归中有广泛的应用。它可以帮助我们更加准确地评估模型的预测能力，避免过度拟合和欠拟合等问题。

• 显著性检验

这部分涉及到数理统计这门课程，头大！快去了解一下吧！

2 简单示例及函数介绍

2.1 sklearn.linear_model&np.array().reshape()

sklearn.linear_model 是 Scikit-learn 模块中的一个子模块，用于实现各种线性模型。该模块中包含许多用于线性回归、岭回归、Lasso回归等任务的类和函数，是Scikit-learn中最基础、最常用的模块之一。

这里我们使用第一个最小二乘法线性回归模型，下方看个示例。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
# 数据集
X = np.array([2, 4, 6, 8, 10]).reshape(-1,1)
Y = [5, 9, 11, 14, 18]
# 模型
model = LinearRegression()
model.fit(X,Y)
# 预测
y_pred=model.predict(X)
# 方程参数
print("系数:",model.coef_)
print("截距:",model.intercept_)
# 绘图
plt.scatter(X,Y)
plt.plot(X,y_pred)
plt.show()
plt.close()

可以发现，上面第四行使用了numpy中的reshape函数，解释下。

在这个代码中，使用 reshape() 函数是为了将一维的自变量 x 转换为二维数组。这是因为 Scikit-learn 中的线性回归模型要求自变量是一个二维数组，其中第一维表示样本数，第二维表示特征数。在一元线性回归的情况下，样本数为自变量的长度，特征数为1。

因此，我们需要将自变量 x 转换为一个列向量，即将原数组的行数不变，将列数变为1。这可以通过 reshape(-1, 1) 来实现，其中 -1 表示自动计算行数。同理，看下方示例：

import numpy as np

arr = np.array([1, 2, 3, 4, 5])
print(arr.shape)      # 输出 (5, )
arr_reshaped = arr.reshape(-1, 1)
print(arr_reshaped.shape)  # 输出 (5, 1)

arr = np.array([1, 2, 3, 4, 5])
print(arr.shape)      # 输出 (5, )
arr_reshaped = arr.reshape(1, -1)
print(arr_reshaped.shape)  # 输出 (1, 5)

2.2 statemodels多元线性回归

import numpy as np
import statsmodels.api as sm
# 创建一个随机的多元线性回归数据集
np.random.seed(0)
n = 100
p = 3
X = np.random.randn(n, p)
y = X.dot(np.array([1, 2, 3])) + np.random.randn(n)
# 向 X 中添加常数项
X = sm.add_constant(X)
# 创建一个多元线性回归模型
model = sm.OLS(y, X)
# 拟合模型并输出结果
results = model.fit()
print(results.summary())

3 实践案例

案例描述：

Walmart是全球最大的连锁超市之一，在全球范围内拥有数千家门店。为了更好地管理门店和制定营销策略，Walmart希望能够预测未来每个门店的销售额，以便做出更好的管理和决策。
数据集：

本实验使用的数据集是Kaggle上的Walmart Dataset (Retail)数据集，包括Walmart公司在2010年2月到2012年10月期间45个店铺的历史销售数据。该数据集包含了多个特征，包括店铺编号、日期、每个店铺每周销售额、是否假期、当日温度、地区燃油价格、消费价格指数（CPI）和失业率等信息。

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 读取数据
df = pd.read_csv('data.csv', parse_dates = True, infer_datetime_format = True)
# 整理数据
df.Date=pd.to_datetime(df.Date)
df['weekday'] = df.Date.dt.weekday
df['month'] = df.Date.dt.month
df['year'] = df.Date.dt.year
df.drop(['Date','weekday','year'], axis=1, inplace=True)
target = 'Weekly_Sales'
# 相关性分析和特征选择
sns.pairplot(df, x_vars=['Holiday_Flag', 'Temperature', 'Fuel_Price', 'CPI', 'Unemployment','month'],
            y_vars=['Weekly_Sales'], height=4, aspect=0.7, kind='reg')
plt.show()

df1=df.copy(deep=True)
df1.drop(['Store'], axis=1, inplace=True)
corr_matrix = df1.corr()
sns.heatmap(corr_matrix, annot=True, cmap='Reds')
plt.show()

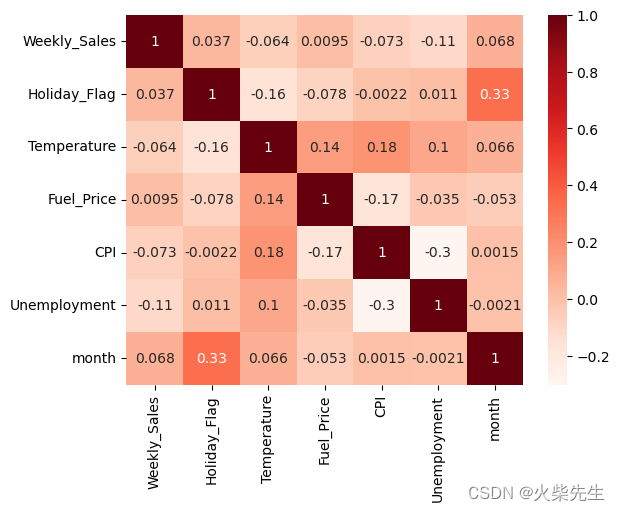
# 发现Fuel_Price和Weekly_Sales的相关系数小于0.01，认为该特征和销售量关系不大
df.drop(['Fuel_Price'], axis=1, inplace=True)
# 分类数据处理
df = pd.get_dummies(df, columns=[ 'Store','month'])
# 提取特征和标签
X = df.drop([target],axis=1)
y = df[target]
# 划分训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=100,test_size=0.2)
# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 训练多元线性回归模型
model = LinearRegression()
model.fit(X_train,y_train)
# 测试集预测
y_pred = model.predict(X_test)
# 评估模型预测效果
print("系数:",model.coef_)
print("截距:",model.intercept_)
print('R平方值(R^2):', r2_score(y_test, y_pred))

参考链接：
机器学习 | 使用statsmodels和sklearn进行回归分析_sklearn statsmodels_育种数据分析之放飞自我的博客-CSDN博客