每日一题 —— 882. 细分图中的可到达节点

882. 细分图中的可到达节点

给你一个无向图（原始图），图中有 n 个节点，编号从 0 到 n - 1 。你决定将图中的每条边细分为一条节点链，每条边之间的新节点数各不相同。

图用由边组成的二维数组 $e d g e s$ 表示，其中 $edges[i] = [u_i, v_i, cnt_i]$ 表示原始图中节点 $u_i $和 $v_i$ 之间存在一条边， $cnt_i$ 是将边细分后的新节点总数。注意， $cnt_i == 0$ 表示边不可细分。

要细分边 $u_i, v_i]$ ，需要将其替换为 $cnt_i + 1)$ 条新边，和 $cnt_i$ 个新节点。新节点为 $x_1, x_2, ..., x_{cnt_i}$ ，新边为 $u_i, x_1], [x_1, x_2], [x_2, x_3], ..., [x_{cnt_i-1}, x_{cnt_i}], [x_{cnti}, v_i]$ 。

现在得到一个 新的细分图 ，请你计算从节点 0 出发，可以到达多少个节点？如果节点间距离是 maxMoves 或更少，则视为 可以到达 。

给你原始图和 maxMoves ，返回 新的细分图 中从节点 0 出发 可到达的节点数 。

示例

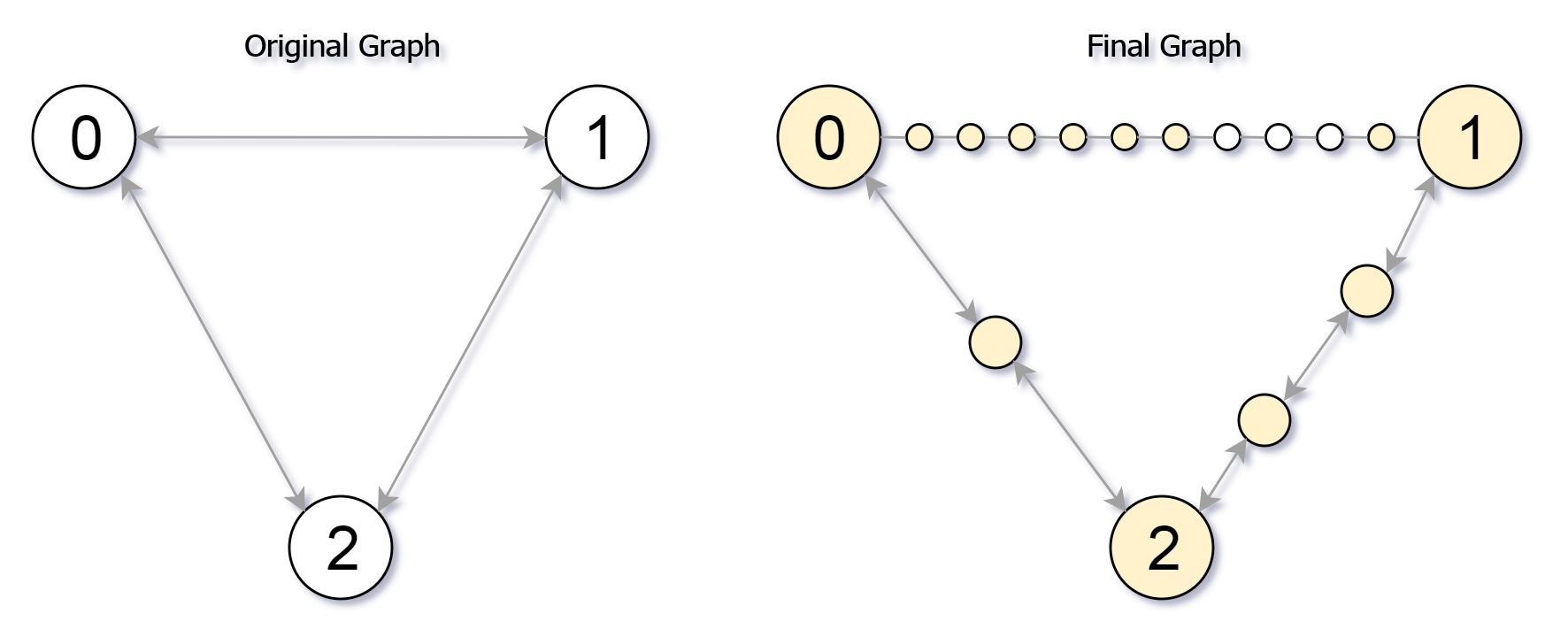
输入：edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出：13
解释：边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。

提示

0 <= edges.length <= min(n * (n - 1) / 2, 10^4)
edges[i].length == 3
$0 <= u_i < v_i < n$
图中 不存在平行边
$0 <= cnt_i <= 10^4$
$0 <= maxMoves <= 10^9$
1 <= n <= 3000

思路

在细分图上操作

首先，考虑能不能暴力做。暴力做，就是先对细分后的图，进行建图，建完图后，原始节点和细分后产生的新节点便没有什么区别。求解从0经过最多maxMoves可到达的节点数，那么只需要用BFS，对每个节点，求一个最短距离（距节点0的距离），然后统计那些距离小于等于maxMoves的节点，进行累加计数即可。思路非常简单。但是看一眼数据范围，发现边最多有 $10^4$ ，每条边上的细分节点数，最多有 $10^4$ ，那么细分节点的总数最大有 $10^8$ ，加上原始节点的3000。细分后的图中的节点数量，会达到 $10^8$ 级别，此时用BFS进行遍历，会访问每个节点一次，则时间复杂度会达到 $10^8$ 级别，是会超时的。所以暴力做法不行。

那么只能在原始图上进行操作。

在原始图上操作

我一开始的思路很naive，就是遍历。（其实从上面暴力思路中能够看出，关键在于求解出每个点到节点0的最短距离，但我一开始的思路只是遍历，还是用DFS遍历的）

具体思路是：从0开始，对原始图进行遍历，对已经走过的点打上标记，以及在访问某个节点时，需要带上剩余的可移动步数。对于边上（假设某条边的2个点为a和b，那么用[a, b]来表示这条边）的细分点，用一个二维数组表示一下，cnt[a][b]表示从a往b走，最多能经过多少个细分点，cnt[b][a]类似。由于从0到某个节点x可能有多条路径，我们当然要选最短的一个，这样的话，当走到x时，剩余的可移动步数才会最大。所以其实，就算是通过遍历，也应当使用BFS，而不是DFS，因为需要求解最短距离。而BFS才具有最短路的特性。

下面是我用BFS提交通过的代码

// C++  540ms
const int N = 3010, M = 2e4 + 10;
typedef pair<int, int> PII;
class Solution {
public:

    int h[N], e[M], ne[M], idx; // 图的邻接表表示

    int cnt[N][N]; // 某个边上的节点数

    int hasMoved[N][N]; // hasMoved[a][b] 表示边[a, b]上, 从a到b方向, 已经访问过的节点数量

    int maxRemain[N]; // maxRemain[a] 表示访问到节点a时，最大的剩余移动步数

    bool st[N]; // 是否已计数过该节点

    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }


    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        memset(h, -1, sizeof h);
        memset(maxRemain, -1, sizeof maxRemain);
        // 建图
        for (auto& e : edges) {
            int a = e[0], b = e[1], c = e[2];
            add(a, b);
            add(b, a);
            cnt[a][b] = cnt[b][a] = c;
        }

        int ans = 0;
        queue<PII> q;
        q.push({0, maxMoves});
        maxRemain[0] = maxMoves;

        while (q.size()) {
            PII p = q.front();
            q.pop();
            int x = p.first, remainMoves = p.second;
            if (maxRemain[x] > remainMoves) continue; // 该节点在队列中有更大的remain, 则跳过该次的计算
            if (!st[x]) {
                ans++;
                st[x] = true;
                //还未计数过该原始节点时, 进行计数 
            }
            // 遍历邻接点
            for (int i = h[x]; i != -1; i = ne[i]) {
                int u = e[i];
                if (remainMoves >= cnt[x][u] + 1) {
                    // 能走过去, 则需要加上整条边上的细分节点数
                    // 但是由于这条边可能之前已经被走过了, 所以需要减掉一些已经走过的节点
                    // 这条线上, 已经走过的节点数, 从左从右都要计算
                    int hasMoveCnt = min(cnt[x][u], hasMoved[x][u] + hasMoved[u][x]);
                    ans += cnt[x][u] - hasMoveCnt; // 答案需要加上那些没走过的节点
                    hasMoved[x][u] = hasMoved[u][x] = cnt[x][u]; // 整条线都被走过, 更新走过的节点数
                    int newRemain = remainMoves - cnt[x][u] - 1; // 走过去后, 剩余的步数
                    if (newRemain > maxRemain[u]) {
                        // 如果当前节点的剩余步数比较大, 则入队列
                        // 当第一次遇到newRemain = 0时, 也需要将u入队, 所以需要初始化maxRemain为-1
                        maxRemain[u] = newRemain;
                        q.push({u, newRemain});
                    }
                } else {
                    // 无法走过去, 则看一下最多能走多少
                    // 因为是双向的, 要减掉重叠部分
                    // 首先看一下对侧走过来的, 走过了多少个节点
                    // 剩余能走的节点数, 要么是remainMoves要么是cnt[x][u] - hasMoved[u][x]
                    int canMaxMoves = min(remainMoves, cnt[x][u] - hasMoved[u][x]);
                    ans += max(0, canMaxMoves - hasMoved[x][u]); // 本侧能走的节点减去本侧已走的节点, 就是新走过的节点
                    hasMoved[x][u] = max(hasMoved[x][u], remainMoves); // 更新本侧走过的节点
                }
            }
        }

        return ans;
    }
};

其实从上面的代码，就能看出，此题其实就是需要求解一个最短路，我们其实可以将每条边上的细分点的个数，看成是这条边的权重。上述BFS在求最短距离时（上面求的是最大剩余步数，其实就是最短距离），对于某一个节点，可能会被多次访问，多次入队。所以效率其实比较低。

只要看出了这道题需要求最短路，并且有意识的把边上的细分点的个数，看成是边的权重，那么很容易就应该想到最短路的经典算法 —— Dijkstra。

因为此题边权都是正数，所以理应用Dijkstra。先用Dijkstra求出0点到每个点的最短距离，然后进行统计

先统计原始图中的点，遍历0到n - 1所有点，当点的距离小于等于maxMoves时进行计数
再统计细分产生的新的点，遍历所有边，查看左右两个的点的最短距离，并计算这条边上的点最多有多少个能被访问到

typedef pair<int, int> PII;
class Solution {
public:

    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        int INF = 1e9;
        vector<int> d(n, INF); // 0号点到所有点的最短距离
        vector<bool> st(n);
        vector<vector<PII>> g(n); // 图的邻接表表示, 存邻接点以及边权
        for (auto& e : edges) {
            int a = e[0], b = e[1], w = e[2];
            g[a].push_back({b, w + 1}); // 边权为节点数加1
            g[b].push_back({a, w + 1});
        }
        // dijkstra
        // 小根堆优化
        priority_queue<PII, vector<PII>, greater<PII>> heap;
        d[0] = 0;
        heap.push({0, 0});
        while (heap.size()) {
            PII p = heap.top();
            heap.pop();
            int node = p.second;
            if (st[node]) continue; // 这个点的最短距离已经被确定了, 跳过
            st[node] = true; // 该点的最短距离已经确定
            // 更新出边
            for(auto& t : g[node]) {
                int u = t.first, w = t.second;
                if (!st[u] && d[u] > d[node] + w) {
                    d[u] = d[node] + w;
                    heap.push({d[u], u});
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            if (d[i] <= maxMoves) ans++;
        }
        for (auto& e : edges) {
            int a = e[0], b = e[1], c = e[2];
            int left = max(maxMoves - d[a], 0); // a往b走最多能走的节点数
            int right = max(maxMoves - d[b], 0); // b往a走最多能走的节点数
            ans += min(left + right, c);
        }
        return ans;
    }
};

另外注意：朴素版的Dijkstra的时间复杂度为 $O(n^2)$ ，堆优化版的Dijkstra的复杂度为 $O (m l o g n)$

（其中 $n$ 是节点数， $m$ 是边数）

当图是稀疏图时（边数较少），适合用堆优化版的Dijkstra

当图是稠密图时（边数非常多， $m$ 基本达到了 $n^2$ 级别），适合用朴素版的Dijkstra

朴素版Dijkstra，建图采用邻接矩阵。一共需要 $n$ 次循环，每次确定一个点的最短距离。在每轮循环内，首先需要遍历 $n$ 个点，从未确定最短距离的点中，找到距离最短的点，随后再更新这个点的所有出边的距离。

外层循环为 $n$ 次
内层循环每次
- 选出当前的最短距离的点（需要遍历所有点，计算量为 $n$ ）
- 更新这个点的全部出边（由于是邻接矩阵表示，实际计算量也是 $n$ ）

所以朴素版Dijkstra复杂度为 $O(n^2)$

堆优化版Dijkstra，建图采用邻接表。一共需要 $n$ 次循环，每次确定一个点的最短距离。在每轮循环内，可以用 $O (1)$ 的开销获取当前距离最短的点，但是需要更新这个点的所有出边的点的距离。

外层循环为 $n$ 次
内层循环
- 每次用 $O (1)$ 选出最短距离的点，但是pop完堆顶后还要调整堆，时间复杂度为 $O (l o g n)$
- 需要更新这个点的所有出边的点的距离（需要插入到堆中，堆会进行调整）

总的来说，需要从堆中取 $n$ 次堆顶。而每走一条边，就可能会更新一个点的距离，整个Dijkstra会访问每条边一次。

我们可以想象为，先把所有点插入到堆中，然后随着算法的进行，每走过一条边，就会更新一个点的距离，这个点在堆中的更新，消耗的时间为 $O (l o g n)$ ，而一共有 $m$ 条边，则需要更新 $m$ 次，则更新的时间复杂度为 $O (m l o g n)$ ，而每次pop出堆顶后，调整堆需要 $O (l o g n)$ ，而一共要pop $n$ 次，所以这部分的复杂度为 $O (n l o g n)$ ，那么总的复杂度是 $O ((n + m) l o g n)$