数据处理

1.导入数据（.csv）

能导入绝大所数形式的格式文件
ex52<-read.table("C:\\Users\\33035\\Desktop\\习题5.2数据.txt",header=T,fileEncoding = 'GBK')
#header ：T:表示留第一行
#fileEncoding:有中文时最好改为GBK

 2.对数据切片获取

ex_52<-ex52[,c(2,4,6,8)]#取这几列做成list

ex_ROAD<-t(ex_52)

 3.把一行变一列数据

ex_52data<-as.vector(t(ex_52))

4. 将数据做成时间序列ts

ex_52series<-ts(ex_52data,start = 1750,frequency = 1)
#参数1：数据
#start:从1750开始
#frequency=1:步进为一年

数据处理已经完成，下面进行时序分析

1.画时序图（初步直观感受时间序列的特性）

plot(ex_52series,type="o")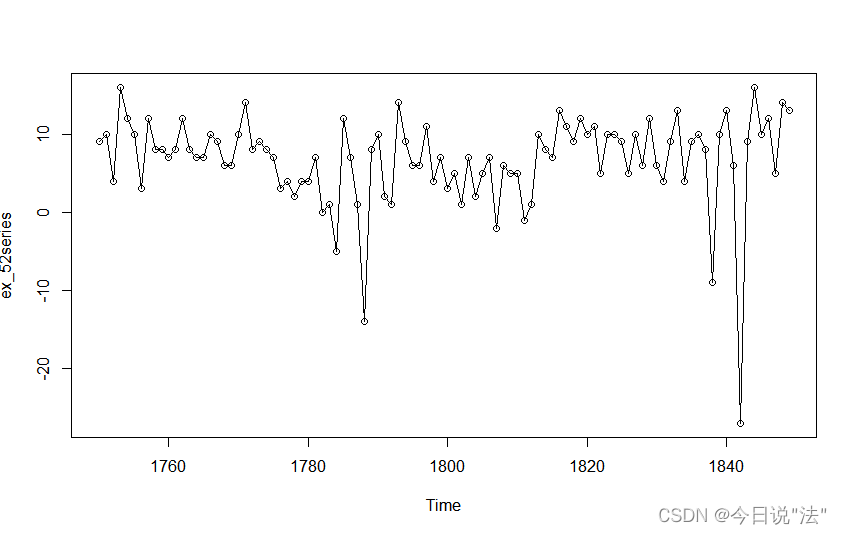

 

看平稳性和白噪声（直观不科学）

非平稳性：有周期性和趋势性

如果存在周期性，那么图像就会有周期性波动，

趋势性：就是有单调性趋势

2. 数据说话：ADF单位根法进行平稳性检验

aTSA::adf.test(ex_52series)#adf检验

结果：

Augmented Dickey-Fuller Test 
alternative: stationary 
 
Type 1: no drift no trend 
     lag    ADF p.value
[1,]   0 -14.52    0.06
[2,]   1 -12.61    0.01
[3,]   2 -14.73    0.06
[4,]   3  -8.42    0.06
Type 2: with drift no trend 
     lag    ADF p.value
[1,]   0 -14.45    0.06
[2,]   1 -12.54    0.01
[3,]   2 -14.65    0.06
[4,]   3  -8.37    0.01
Type 3: with drift and trend 
     lag    ADF p.value
[1,]   0 -14.38    0.06
[2,]   1 -12.48    0.06
[3,]   2 -14.64    0.06
[4,]   3  -8.41    0.01
---- 
Note: in fact, p.value = 0.01 means p.value <= 0.06 

3种类型的ADF检验结果，但我们只需要关注最后的 means p.value <= 0.06 即可，只要<0.05即显著，什么显著呢？（不同假设，就有不同类型的显著）平稳性显著

3.显然不显著，那么就进行差分（逐步差分，每步差分都要进行白噪声检验，避免过差分）

如果是存在周期性就以周期T为步数，作为T步差分

delatex_52series<-diff(ex_52series)#做一阶一步差分

3.1进行白噪声检验（延迟阶数24内就行，因为只需要推翻短期相关性）

#白噪声检验
for(i in 1:4){
  Box=Box.test(delatex_52series,lag = 3*i,type="Ljung-Box")
  print(Box)}
#通过白噪声检验，表示该序列纯随机序列(推翻短期相关性即可)

 平稳序列具有短期相关性，只要短期都不相关，那么久处处不相关了

#白噪声和ACF和PACF其实都是在说相关性
#P<0.5白噪声不显著
#得到了平稳非白噪声序列，进入定阶段环节

 结果：

    Box-Ljung test

data:  delatex_52series
X-squared = 20.982, df = 3, p-value = 0.0001062

    Box-Ljung test

data:  delatex_52series
X-squared = 45.155, df = 6, p-value = 4.359e-08

    Box-Ljung test

data:  delatex_52series
X-squared = 49.727, df = 9, p-value = 1.212e-07

    Box-Ljung test

data:  delatex_52series
X-squared = 50.516, df = 12, p-value = 1.134e-06

看P值即可，看所有的K，只要小于<0.05就表示非白噪声.很显然都是非白噪声，那么表示差分后还具有研究价值

4.得到平稳和非白噪声序列，那么就能进入定阶阶段

定阶阶段：直观：ACF （q阶截尾）和PACF（p阶截尾）：定阶只看截尾（横坐标：为延迟期数

纵坐标：为两个时间点的相关系数）

acf(delatex_52series)#拖尾
pacf(delatex_52series)#3阶截尾

 结果：

 

 

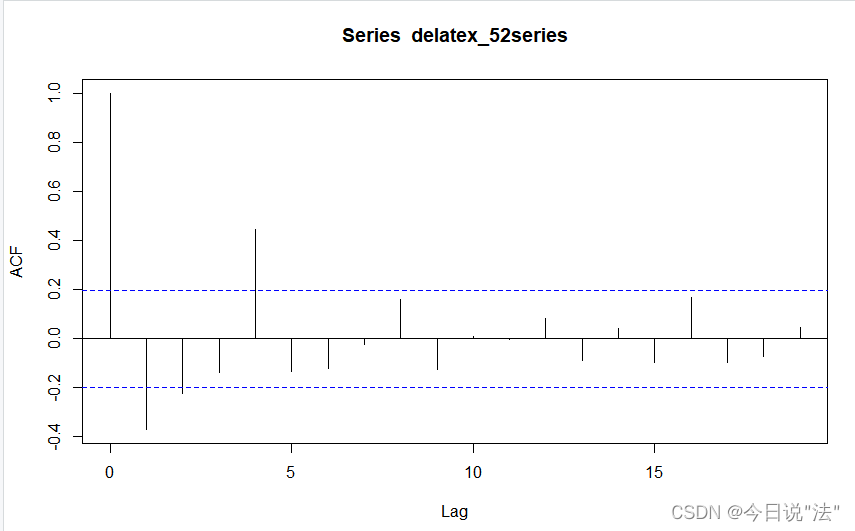
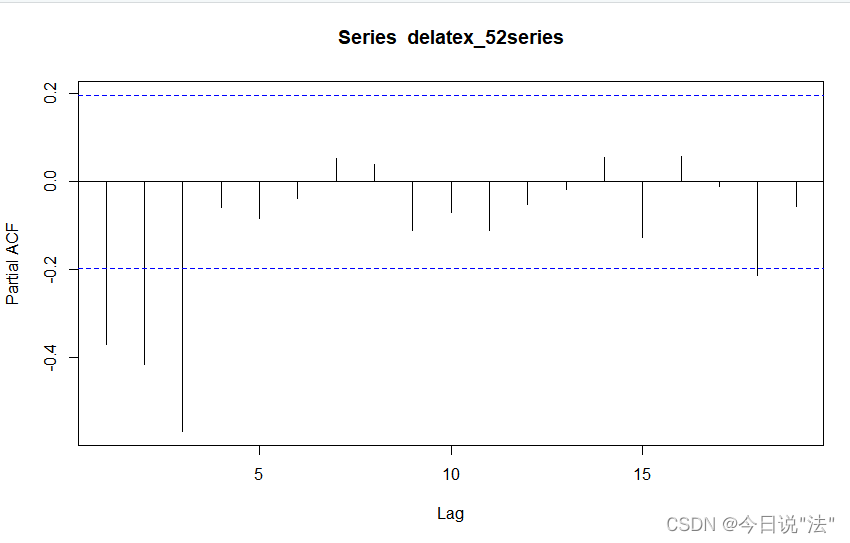
数据：AIC 和BIC准则：要求是找出AIC和BIC的max值时对应的阶数（p,q）(原理是阶数越高，描述得越详细越符合现实，但是参数会变多，会增加难度，所以就是让阶数合理，就是让AIC和BIC的式子达到最大值)

 

#数据定阶段AIC和BIC
#选取最大的AIC或者BIc值的模型，小心于系数要大于2标准差，才是显著有关系（非0）
install.packages('forecast')
library(forecast)
auto.arima(delatex_52series,max.p=6,max.q=6,ic="aic")#选择AR(3)模型

最大的p值 ，最大的q值：一般都=6即可，默认为5，ic:aic bic 还有另外一个不需要理

结果：告诉我要选AR(3),ARIMA(p(看pacf),d(阶数),q(看pac)),另外会给出3个系数，下面是s.e是

样本标准差，这里要保证系数要大于2*样本标准差，不然表示相关关系不显著。

结果：

Series: delatex_52series 
ARIMA(3,0,0) with zero mean 

Coefficients:
          ar1      ar2      ar3
      -0.7603  -0.7078  -0.5705
s.e.   0.0818   0.0850   0.0816

sigma^2 = 30.25:  log likelihood = -308.58
AIC=625.15   AICc=625.58   BIC=635.53

这里就已经是选好了模型了。下面要做的就是进行模型的拟合和模型的显著性检验

5.模型拟合：

#有差分运算时采用有漂移项预测更准确Arima
#无差分运算时用arima
f1<-arima(delatex_52series,order=c(3,0,0))

 结果：（与上面AIC定阶一样，不过这是知道阶数才用的，不知道阶数检验用上面的来拟合）

> f1<-arima(delatex_52series,order=c(3,0,0))
> f1

Call:
arima(x = delatex_52series, order = c(3, 0, 0))

Coefficients:
          ar1      ar2      ar3  intercept
      -0.7603  -0.7078  -0.5705     0.0186
s.e.   0.0818   0.0850   0.0816     0.1815

sigma^2 estimated as 29.34:  log likelihood = -308.57,  aic = 627.14

 Arima的最后一个参数改为T，即可。其实区别就在这个参数而已，但是Arima拟合的模型对象不能作为LB检验的对象，arima可以。

6.模型的有效的显著检验（首先我们拟合出来的模型会产生一个新时序，与旧时序的误差，我们拿这误差来分析，显然模型有效就代表能百分百拟合旧序列，也就是说新时序和旧时序是一样的。误差全为随机误差，也就是白噪声序列，那么只要证明它是白噪声序列即可说明模型有效。证明白噪声序列的话有BOX、Q检验和Q检验的加强版（LB检验），我们使用LB检验）

aTSA::ts.diag(f1)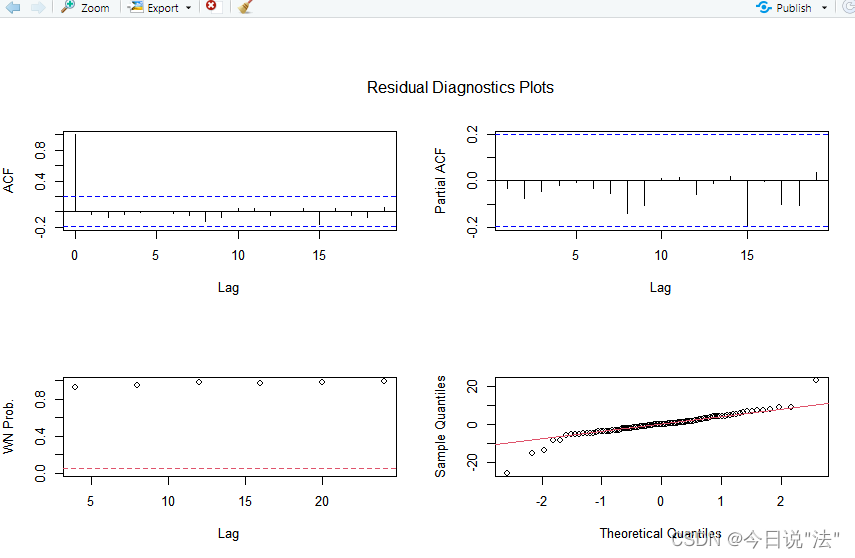

 第一acp和第二个图pacp:如果模型不能通过显著性检验，就可以重新定阶段

第三个图：残差序列白噪声检验图，x为lag,y为Q统计量的P值，要都大于0.05才能说明是白噪声

第四个图：QQ图，y是正态分布的概论分布值,x为残差的概论分布值，只要点集中在y=x，就说明残差服从正态分布。正态分布是白噪声序列的特征

7.发现模型有效之后，就可以拿来预测了。

#拟合好模型后可以进行预测了
library(forecast)
fore<-forecast(f1,h=5)#预测前五期的数据
fore
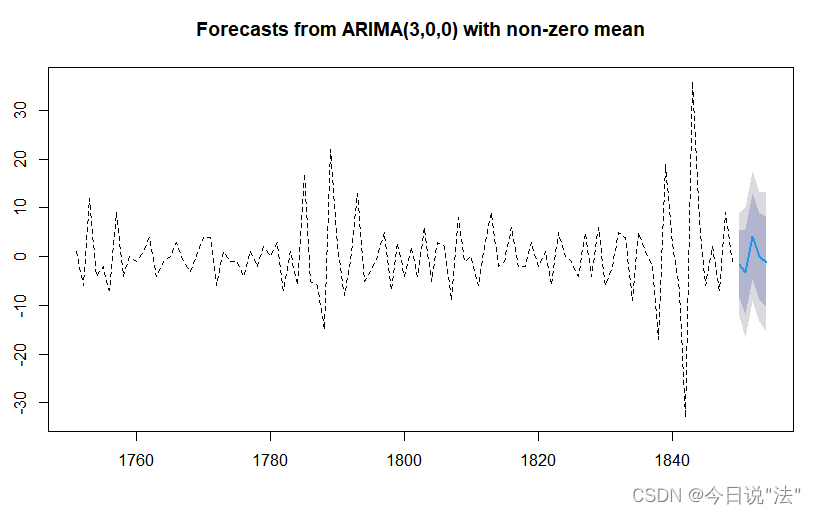
plot(fore,lty=2)#虚线

      Point Forecast      Lo 80     Hi 80      Lo 95     Hi 95
1850    -1.56005365  -8.501169  5.381062 -12.175574  9.055467
1851    -3.18400834 -11.903549  5.535532 -16.519395 10.151378
1852     4.15225821  -4.613679 12.918195  -9.254086 17.558602
1853     0.04340675  -8.734613  8.821427 -13.381416 13.468230
1854    -1.09900488 -10.476245  8.278235 -15.440256 13.242246

 

蓝线是点估计 深色为80%置信区间  浅色为95%的置信区间 

代码汇总：（有点不符合上述流程，懒得改了）

ex52<-read.table("C:\\Users\\33035\\Desktop\\习题5.2数据.txt",header=T,fileEncoding = 'GBK')
ex_52<-ex52[,c(2,4,6,8)]
ex_ROAD<-t(ex_52)
ex_52data<-as.vector(t(ex_52))
ex_52series<-ts(ex_52data,start = 1750,frequency = 1)
plot(ex_52series,type="o")
delatex_52series<-diff(ex_52series)#做一阶一步差分
plot(delatex_52series,type="o")#画时序图
aTSA::adf.test(delatex_52series)#adf检验
#白噪声检验
for(i in 1:4){
  Box=Box.test(delatex_52series,lag = 3*i,type="Ljung-Box")
  print(Box)}
#通过白噪声检验，表示该序列纯随机序列(推翻短期相关性即可)
#白噪声和ACF和PACF其实都是在说相关性
#P<0.5白噪声不显著
#得到了平稳非白噪声序列，进入定阶段环节
acf(delatex_52series)#拖尾
pacf(delatex_52series)#3阶截尾，19阶后又出现（有问题得看答案）
#数据定阶段AIC和BIC
#选取最大的AIC或者BIc值的模型，小心于系数要大于2标准差，才是显著有关系（非0）
install.packages('forecast')
library(forecast)
auto.arima(delatex_52series,max.p=6,max.q=6,ic="aic")#选择AR(3)模型
#进行拟合
#ar 和 ma 和arma模型选择（已经知道定价之后）
#有差分运算时采用有漂移项预测更准确Arima
#无差分运算时用arima
f1<-arima(delatex_52series,order=c(3,0,0))
f1
#拟合好模型后可以进行预测了
library(forecast)
fore<-forecast(f1,h=5)#预测前五期的数据
fore
plot(fore,lty=2)#虚线
#进行模型评估
win.graph(width = 5,height = 5)#新建一个画布
aTSA::ts.diag(f1)