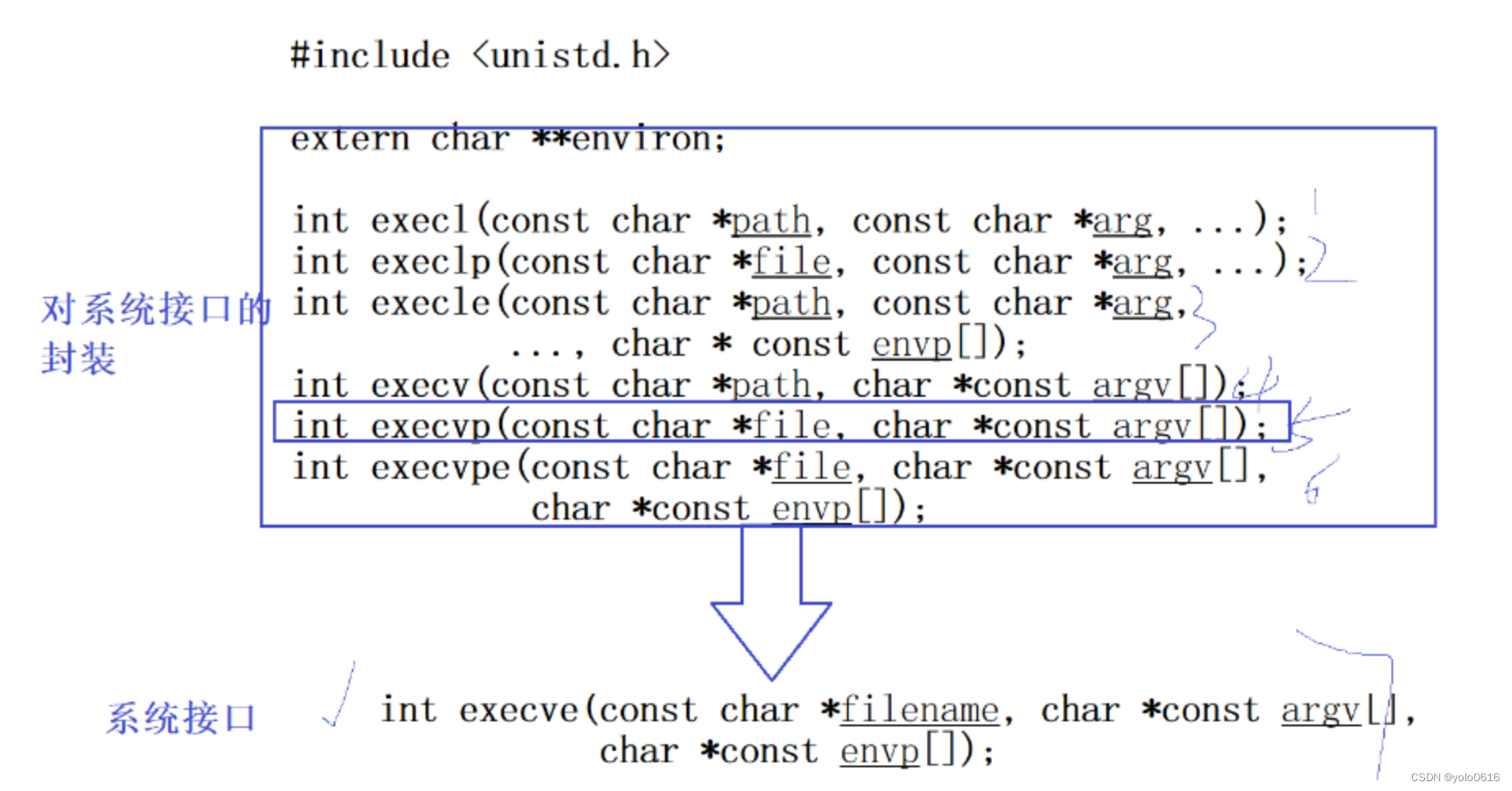
概述

• 目的在原有大模型上进行fine tune，训练个性化模型

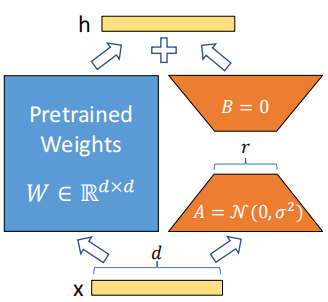
• idea：将pretrained model参数冻住，额外训练一个module进行调整，最终输出是原始输出+经过module的输出。
  

• 技巧：通过低秩分解大大降低了需要训练参数的数量。矩阵分解：对于一个$m\ast n$的矩阵，若它的秩是r，则可以通过$m\ast r$和$r\ast n$的矩阵近似

方法

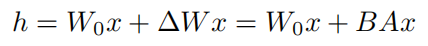
• $W_0$是预训练模型的参数，$△W$是添加module的参数，$x$是输入。注意这里$A$为高斯随机初始化，$B$初始化为0，这样一开始$△W=0$，整个模型的输出与预训练模型一样，有利于模型的收敛
• 这里只对attention层中的参数进行矩阵分解，包括$W_q,W_k,W_v,W_o$
• 当r=d的时候，就相当于对所有参数进行微调
• 没有额外的inference延迟，因为最后计算的时候可以先让$W_0$和$△W$相加，然后再乘x，与之前直接和x相乘的计算量差不多

实验

• 为什么lora效果好？即使是fine tune所有的参数，得到的$△W$矩阵的秩也是很低的，因此可以做低质分解降低需要训练的参数量
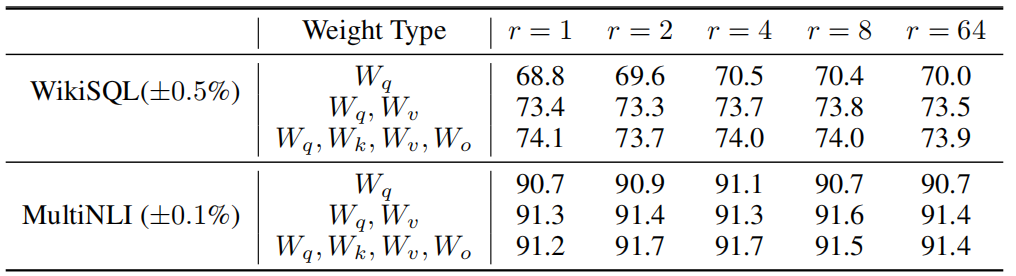
• 矩阵分解的位置。实验发现在总参数量保持一致的情况下施加在4个参数上效果最好，单独施加效果最差
  
• r的选择。在nlp任务上，r取4能够得到较好的效果。作者也通过实验说明当r较小时与较大的r能够有很高的相似性。q矩阵的秩高于v矩阵的秩
  
• $△W$放大了$W$在某些方向上的表达（下游任务中需要的某些方向）

注意

• 在实验中作者为了简单只对$w_q$和$W_v$进行分解
• lora在小样本fine tune上的效果很好（10k以下）