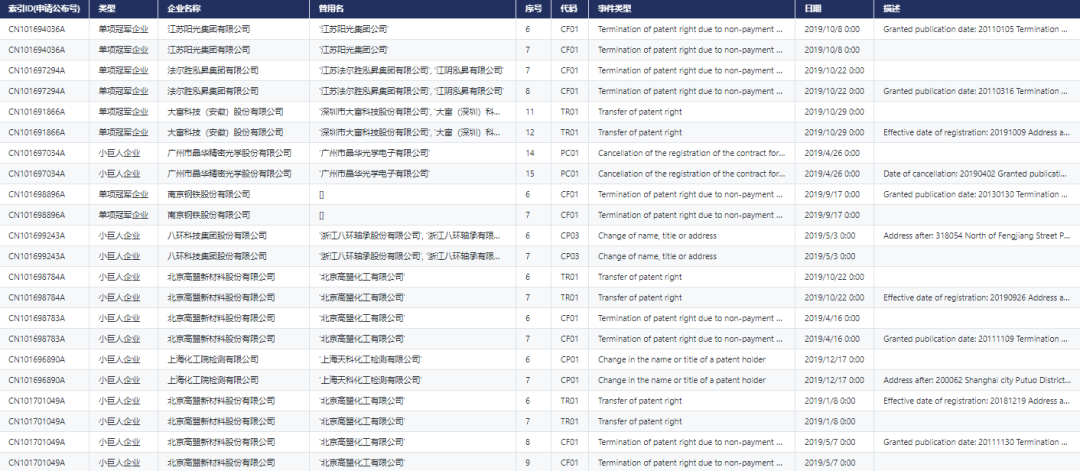
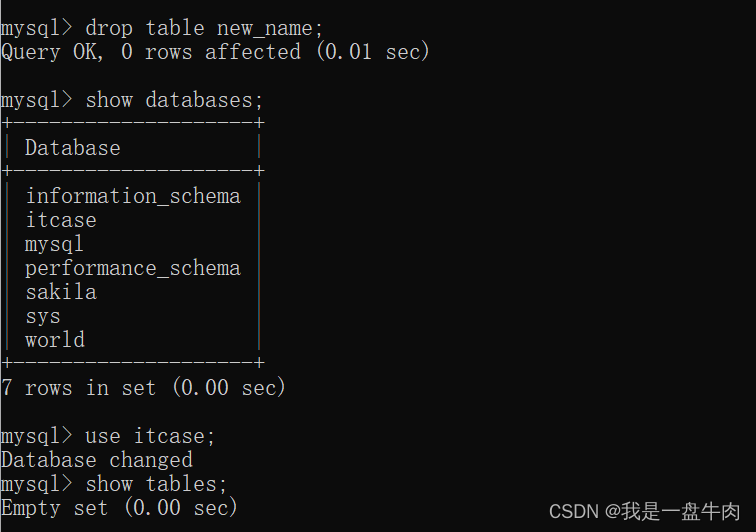
1.三大抽样分布

本人博客：总体分布、样本分布、抽样分布的区别

每一个样本统计量（本质是随机变量）都有一个分布

以样本平均数为例，它是总体平均数的一个估计量，如果按照相同的样本容量，相同的抽样方式，反复地抽取样本，每次可以计算一个平均数，所有可能样本的平均数所形成的分布，就是样本平均数的抽样分布 --摘自：抽样分布

1.1 卡方分布（${\chi }^2$分布）

自由度指的是用来计算统计量的观测数据（变量）中可以自由取值的数据的个数。
自由度=样本容量-限制条件数
限制条件数就是使用了样本数据的计算公式的个数

下图来自《统计学图鉴》

卡方分布构造
设$X_1,X_2\cdots X_n$独立同$N(0,1)$分布
$$\begin{gathered} X_i\sim N(0,1) \\ {\chi }^2=X_1^2+X_2^2+\cdots +X_n^2=\sum _{i=1}^n{X}_i^2\sim {\chi }^2(n) \\ \text{DoF=n} \end{gathered}$$
下图来自：Chi-squared distribution

卡方分布性质
数字特征：$X\sim N(0,1)$ 则 ${\chi }^2\sim {\chi }^2(n)，E(X^2)=n，D(X^2)=2n$

可加性：${\chi }_1^2\sim {\chi }^2(n_1)，{\chi }_2^2\sim {\chi }^2(n_2)$ 且 ${\chi }_1^2$ 与 ${\chi }_2^2$ 相互独立，则 ${\chi }_1^2+{\chi }_2^2\sim {\chi }^2(n_1+n_2)$

卡方分布分位点 ${\chi }_{\alpha }^2(n)$（自由度为n的${\chi }^2$的上侧$\alpha$分位点）

1.2 t分布

构造：$X\sim N(0,1)，Y\sim {\chi }^2(n)$且$X、Y$独立，则
$$T=\frac{X}{\sqrt{\frac{Y}{n}}}\sim t(n)$$
下图来自：Student’s t-distribution

t分布的性质：

t分布的分位点

1.3 F分布

构造：${\chi }^{\sim }{\chi }^2(n_1)，Y\sim {\chi }^2(n_2)$ 且$X、Y$独立，则
$$F=\frac{\frac{X}{n_1}}{\frac{Y}{n_2}}\sim F(n_1,n_2)$$
下图来自：F-distribution

性质

F分布分位点

1.4 三大抽样分布的关系