来源:力扣(LeetCode)
描述:
给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ,返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。
如果行和列以相同的顺序包含相同的元素(即相等的数组),则认为二者是相等的。
示例 1:

输入:grid = [[3,2,1],[1,7,6],[2,7,7]]
输出:1
解释:存在一对相等行列对:
- (第 2 行,第 1 列):[2,7,7]
示例 2:
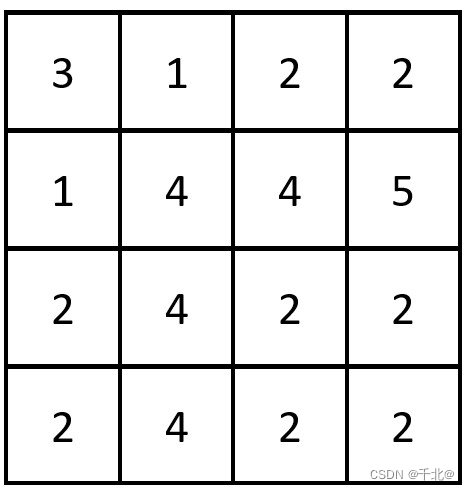
输入:grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出:3
解释:存在三对相等行列对:
- (第 0 行,第 0 列):[3,1,2,2]
- (第 2 行, 第 2 列):[2,4,2,2]
- (第 3 行, 第 2 列):[2,4,2,2]
提示:
- n == grid.length == grid[i].length
- 1 <= n <= 200
- 1 <= grid[i][j] <= 105
方法一:模拟
思路
按照题目要求,对任意一行,将它与每一列都进行比较,如果相等,则对结果加一,最后返回总数。
代码:
class Solution {
public:
int equalPairs(vector<vector<int>>& grid) {
int res = 0, n = grid.size();
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
if (equal(row, col, grid)) {
res++;
}
}
}
return res;
}
bool equal(int row, int col, vector<vector<int>>& grid) {
int n = grid.size();
for (int i = 0; i < n; i++) {
if (grid[row][i] != grid[i][col]) {
return false;
}
}
return true;
}
};
执行用时:320 ms, 在所有 C++ 提交中击败了19.91%的用户
内存消耗:22.7 MB, 在所有 C++ 提交中击败了98.50%的用户
复杂度分析
时间复杂度:O(n3),需要进行双层循环,每次循环最多需要遍历 n 个数字。
空间复杂度:O(1),仅使用常数空间。
方法二:哈希表
思路
首先将矩阵的行放入哈希表中统计次数,哈希表的键可以是将行拼接后的字符串,也可以用各语言内置的数据结构,然后分别统计每一列相等的行有多少,求和即可。
代码:
class Solution {
public:
int equalPairs(vector<vector<int>>& grid) {
int n = grid.size();
map<vector<int>, int> cnt;
for (auto row : grid) {
cnt[row]++;
}
int res = 0;
for (int j = 0; j < n; j++) {
vector<int> arr;
for (int i = 0; i < n; i++) {
arr.emplace_back(grid[i][j]);
}
if (cnt.find(arr) != cnt.end()) {
res += cnt[arr];
}
}
return res;
}
};
执行用时:64 ms, 在所有 C++ 提交中击败了98.65%的用户
内存消耗:33 MB, 在所有 C++ 提交中击败了48.20%的用户
复杂度分析
时间复杂度: O(n2),将行放入哈希表中消耗 O(n2),读所有列的哈希表中的次数也消耗 O(n2)。
空间复杂度:O(n2),哈希表的空间复杂度为 O(n2)。
author:LeetCode-Solution