文章目录
- Delaunay三角剖分学习笔记
- 1 Voronoi \text{Voronoi} Voronoi图
- 1.1 定义与性质
- 2 三角剖分
- 2.1 定义与性质
- 2.2 质量(quality)评定标准
- 3 Delaunay三角剖分
- 3.1 定义
- 3.2 准则与性质
- 4 Delaunay三角剖分算法
- 4.1 Bowyer-Watson算法
- 4.1.1 算法步骤:
- 4.1.2 算法伪代码
- 4.1.3 算法解释示例
- 4.1.4 算法的优化
- (1)排序优化
- (2)快速点定位
- 4.1.5 实现细节
- (1)构造超级三角形
- (2)计算三角形外接圆圆心和半径
- 4.1.6 代码实现
- 4.2 分治法
- 4.2.1 Quad-Edge
- (1)create_edge(org, dest, edges)
- (2)update_next_prev(e1, e2)
- (3)connect(e1, e2, edges)
- (4)mark_edge_deleted(e)
- 4.2.2 工具算法
- (1)判断点是否在三角形外接圆内
- (2)判断点与边的相对位置
- 4.2.3 主要程序
Delaunay三角剖分学习笔记
1 Voronoi \text{Voronoi} Voronoi图
在理解Delaunay三角剖分之前,先引入 Voronoi \text{Voronoi} Voronoi图。
1.1 定义与性质
定义
设由任意 n n n个互异平面点(也称基点)组成的点集 P = { p i ∣ i = 1 , . . . , n } P=\{p_i|i=1,...,n\} P={pi∣i=1,...,n}。 P P P对应的 Voronoi \text{Voronoi} Voronoi图可以理解为对平面的一个区域(单元)划分。对于划分得到的每个区域(也称 Voronoi \text{Voronoi} Voronoi多边形),都应当满足:在基点 p i p_i pi对应的单元中任取一点,该点到 p i p_i pi的(欧式)距离一定小于到 p j , p j ∈ P , j ≠ i p_j,p_j\in{P},j\ne{i} pj,pj∈P,j=i的(欧式)距离。
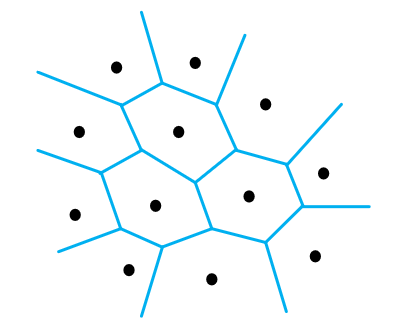
Voronoi \text{Voronoi} Voronoi又称泰森多边形或 Dirichlet \text{Dirichlet} Dirichlet图。
平面上的 V-图可以看作是数据点集合 P 中的每个点作为生长点,以相同的速率向 外扩散,直到彼此相遇为止在平面上所形成的图形。除最外层的点形成开放的区域外, 其余的每个点都形成一个凸多边形。
一些性质
- 每个 Voronoi \text{Voronoi} Voronoi多边形内仅包含一个基点;
- Voronoi \text{Voronoi} Voronoi多边形内的任一点到相应基点的(欧式)距离最近;
- 位于 Voronoi \text{Voronoi} Voronoi多边形边上的点到其两边的离散点的距离相等;
- n n n个点的集合 P P P的 Voronoi \text{Voronoi} Voronoi图最多有 2 n − 5 2n-5 2n−5个顶点和 3 n − 6 3n-6 3n−6条边;
- 假如任意四个基点都不共圆,则每个 Voronoi \text{Voronoi} Voronoi顶点恰好是三条 Voronoi \text{Voronoi} Voronoi边的交点,即由 P P P中的三点所形成三角形外接圆的圆心。
参考:
[1] 高莉. 改进的Delaunay三角剖分算法研究[D]. 兰州交通大学, 2015.
[2] 泰森多边形_百度百科 (baidu.com)
2 三角剖分
2.1 定义与性质
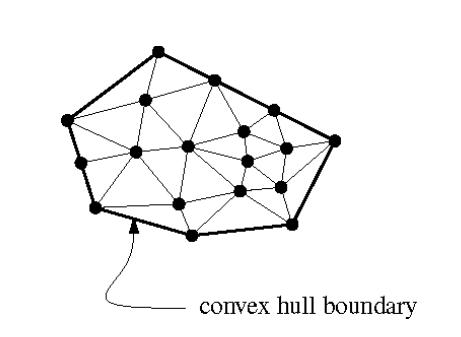
设由任意 n n n个平面点组成的点集 P = { p i ∣ i = 1 , . . . , n } P=\{p_i|i=1,...,n\} P={pi∣i=1,...,n}。三角剖分是指用互不相交的直线段连接 P i P_i Pi与 P j P_j Pj, 1 ≤ i , j ≤ n , i ≠ j 1≤i,j≤n,i≠j 1≤i,j≤n,i=j,并且使其凸包中的每个划分区域都是一个三角形。
由于三角剖分是一个平面图,故满足以下几个条件:
- 图中不存在相交的边(除线段端点外,不存在重叠的边);
- 图中的边不包含集合 P P P中的其他任何点,端点除外;
- 图中所有的面片都是三角形,并且所有三角形的集合构成 P P P的凸包。
2.2 质量(quality)评定标准
由于对给定点集的三角剖分不唯一,对于不同的三角剖分我们有如下质量评定标准:
| 质量评定标准 | 解释 |
|---|---|
| 最小角(minimum angle) | 所有三角形的内角当中最小的角 |
| 纵横比(aspect ratio) | 三角形最短边与最长边的比例 |
| 半径比(radius ratio) | 三角形内接圆半径的两倍与外接圆半径的比例 |
参考:
[1] 技术分享:Delaunay三角剖分算法介绍 - 知乎 (zhihu.com)
3 Delaunay三角剖分
Delaunay剖分是一种三角剖分的标准。
3.1 定义
Delaunay边:假设 E E E( E E E为点集的三角剖分的边集)中的一条边 e e e(两个端点分别为 a , b a,b a,b), e e e为Delaunay边的条件为:存在一个圆经过 a , b a,b a,b两点,圆内(最多三点共圆)不含点集 P P P中任何其他的点,这一特性又称空圆特性。
Delaunay三角剖分:如果点集 P P P的一个三角剖分 T T T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。
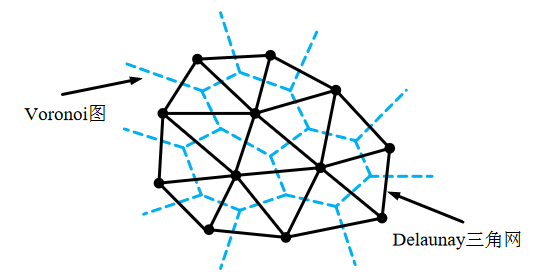
Delaunay三角剖分的另一种定义:因为Delaunay三角剖分与 Voronoi \text{Voronoi} Voronoi图是对偶关系,Delaunay三角剖分是 Voronoi \text{Voronoi} Voronoi图的伴生图形,两者可以相互转化。作 Voronoi \text{Voronoi} Voronoi图的对偶图,即对每条 Voronoi \text{Voronoi} Voronoi边(限有限长线段)作通过点集中某两点的中垂线,得到的即为Delaunay三角剖分。
3.2 准则与性质
一个三角剖分必须符合以下两条重要准则,才可称之为Delaunay三角剖分。
-
空圆特性
Delaunay三角剖分是唯一的(任意四点不能共圆),在Delaunay三角剖分中任一三角形的外接圆内不会存在其它点。即满足Delaunay边的定义。
-
最大化最小角特性
在点集 P P P的所有可能的三角剖分中,Delaunay三角剖分所形成的三角形最小角最大。
Delaunay三角剖分具备以下几点重要的性质:
(1)唯一性:无论从点集的任何位置开始建网,最终得到的Delaunay三角剖分都是唯一的。
(2)最接近:三角形是以最邻近的三点组成的,并且所形成的三角形的各边都不会相交。
(3)最规则:假如将三角剖分中每个三角形的最小角度按升序进行排列,那么Delaunay三角剖分排列得到的数值最大。
(4)最优性:如果任意两个相邻三角形所组成的凸四边形的对角线相互交换,那么交换后两个三角形的六个内角中最小角角度不再增大。
(5)区域性:移动、新增、删除三角剖分中某个顶点时只会影响相邻的三角形。
(6)具有凸多边形的外壳:在所构建的三角剖分中,最外层的边界构成了点集的凸多边形“外壳”(即点集的凸包)。
4 Delaunay三角剖分算法
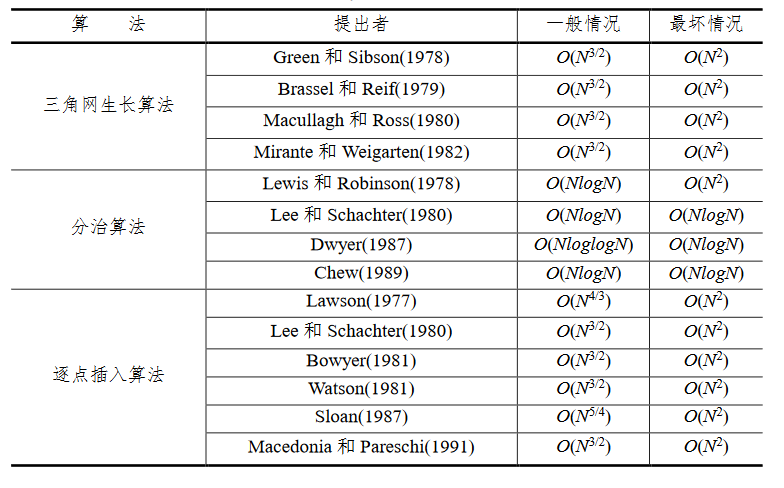
Delaunay三角剖分的算法可以分为逐点插入法、三角网生长法,分治算法等。分治算法的效率最高,逐点插人法实现简单高效,占用内存较小,但它的时间复杂度差。三角网生长法由于效率相对较低,目前采用较少。
4.1 Bowyer-Watson算法
Bowyer-Watson算法属于逐点插入法的一种,易于理解和实现。
4.1.1 算法步骤:
Step1:构造一个包含点集中的所有点的超级三角形(super-triangle),放入三角形列表中;
这个三角形列表可以理解为一个三角剖分,目前只包含一个三角形,即超级三角形。
Step2:将点集中的点逐一插入现有的三角剖分中,并进行如下调整:
-
在三角形列表中,找出所有外接圆包含该插入点的三角形(称为该点的影响三角形),所有影响三角形的合集构成一个“星形多边形”(star shaped polygon)。星形多边形的含义是多边形的任何一个顶点到插入点的连线都在多边形内部。
-
对于上述星形多边形,将其内部的三角形全部删除,形成一个“空穴”。将空穴边界的顶点与新插入的点连接得到新的三角形,替代剖分中被删除的三角形,从而完成一个点在Delaunay三角形列表中的插入,得到一个包含插入点的新Delaunay三角剖分。
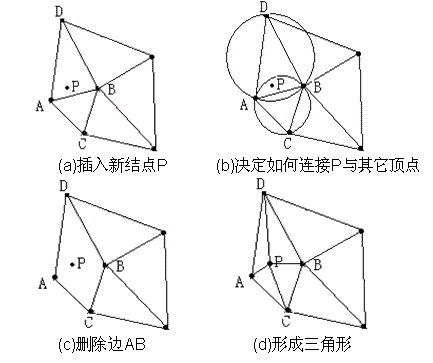
还有一种说法是:在三角形列表中,找出其外接圆包含插入点的三角形(称为该点的影响三角形),删除影响三角形的公共边,将插入点同影响三角形的全部顶点连接起来,从而完成一个点在Delaunay三角形列表中的插入。该步骤的图示如下:
Step3:循环执行Step2,直到所有点插入完毕。
Step4:最后从三角形列表中删除与超级三角形关联的三角形,得到点集的Delaunay三角剖分。
4.1.2 算法伪代码
版本一
from Triangulate: Pan Pacific Computer Conference, Beijing, China (paulbourke.net)
input : vertex list
output : triangle list
initialize the triangle list
determine the supertriangle
add supertriangle vertices to the end of the vertex list
add the supertriangle to the triangle list
for each sample point in the vertex list
initialize the edge buffer
for each triangle currently in the triangle list
calculate the triangle circumcircle center and radius
if the point lies in the triangle circumcircle then
add the three triangle edges to the edge buffer
remove the triangle from the triangle list
endif
endfor
delete all doubly specified edges from the edge buffer
this leaves the edges of the enclosing polygon only
add to the triangle list all triangles formed between the point
and the edges of the enclosing polygon
endfor
remove any triangles from the triangle list that use the supertriangle vertices
remove the supertriangle vertices from the vertex list
end
版本二
from Bowyer–Watson algorithm - Wikipedia.
function BowyerWatson (pointList)
// pointList is a set of coordinates defining the points to be triangulated
triangulation := empty triangle mesh data structure
add super-triangle to triangulation // must be large enough to completely contain all the points in pointList
for each point in pointList do // add all the points one at a time to the triangulation
badTriangles := empty set
for each triangle in triangulation do // first find all the triangles that are no longer valid due to the insertion
if point is inside circumcircle of triangle
add triangle to badTriangles
polygon := empty set
for each triangle in badTriangles do // find the boundary of the polygonal hole
for each edge in triangle do
if edge is not shared by any other triangles in badTriangles
add edge to polygon
for each triangle in badTriangles do // remove them from the data structure
remove triangle from triangulation
for each edge in polygon do // re-triangulate the polygonal hole
newTri := form a triangle from edge to point
add newTri to triangulation
for each triangle in triangulation // done inserting points, now clean up
if triangle contains a vertex from original super-triangle
remove triangle from triangulation
return triangulation
4.1.3 算法解释示例
这里我们以A,B,C,D四个点为例,画图说明整个Bowyer-Watson算法的流程。
-
首先建立一个超级三角形(p1,p2,p3),这个三角形要把点集中所有的点都包含进去。将这个超级三角形加入三角形列表。
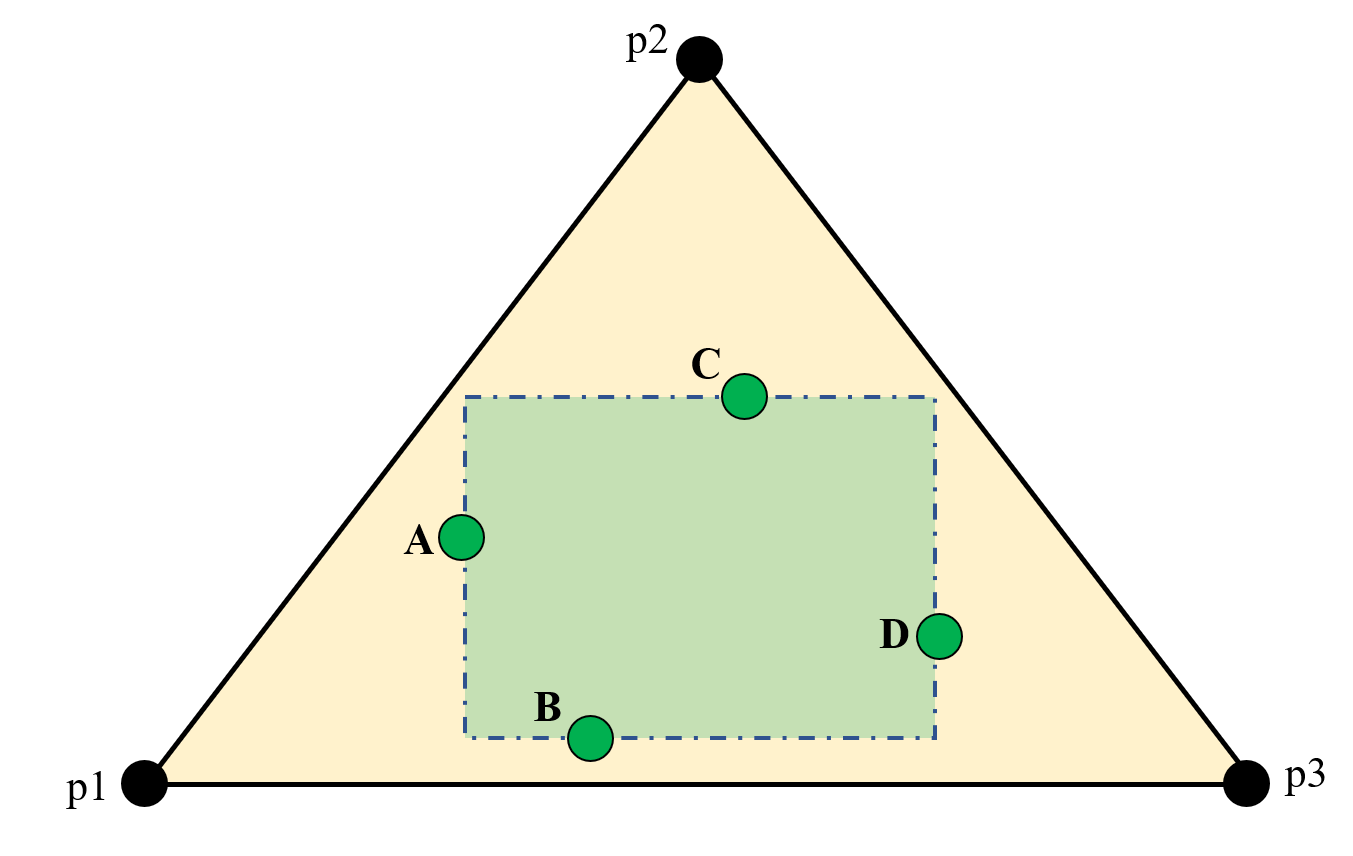
关于如何构建超级三角形,详见[4.1.5 实现细节](#4.1.5 实现细节)。
-
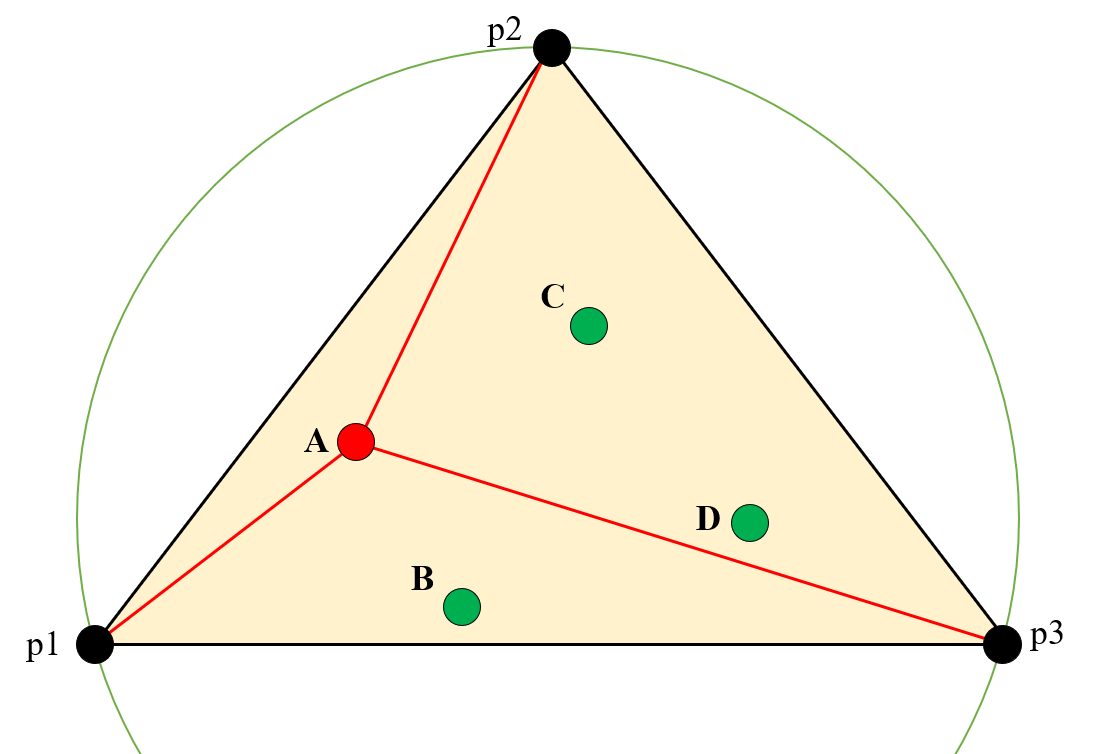
我们先插入点A,因为原来的三角形列表中唯一的超级三角形外接圆必定包含点A,所以我们可以将三角形▲(p1,p2,p3)看作一个星形多边形,其内部没有三角形,所以我们直接将点A与其顶点相连,将原来的三角形拆分为三个三角形(▲(p1,A,p2),▲(p2,A,p3),▲(p3,A,p1))。
-
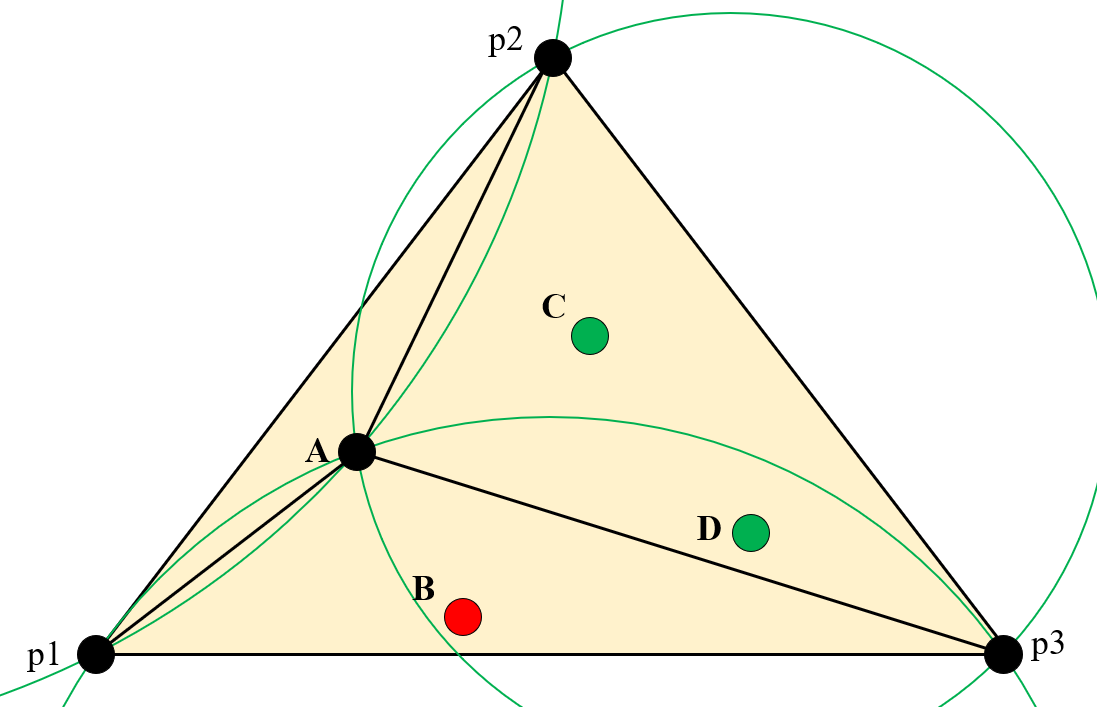
再插入点B,做三角形列表中各个三角形的外接圆,我们找到了点B的影响三角形,即▲(p1,A,p3),▲(p2,A,p3)。
-
删除影响三角形组成的星形多边形内部的三角形(公共边,这里即边(A,p3))。然后将点B同影响三角形的全部顶点连接起来。
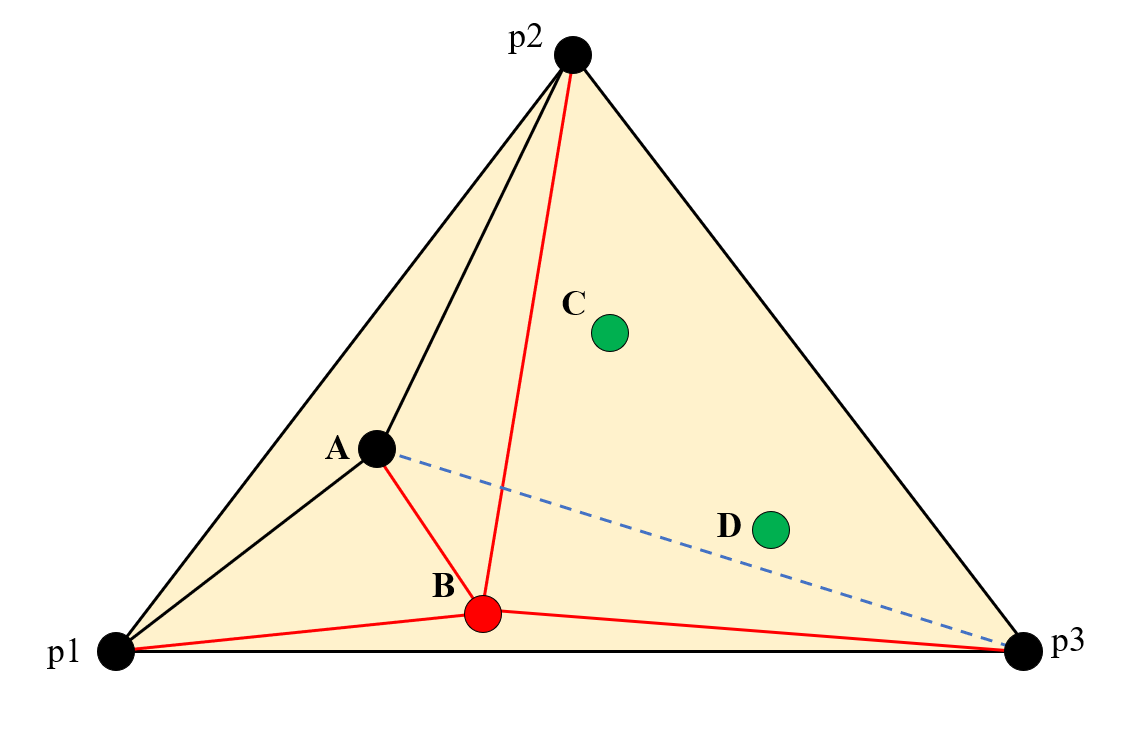
-
接下来再插入点C,同上面插入点B的流程一样,找到影响三角形,删除公共边,连接影响三角形的各个顶点。
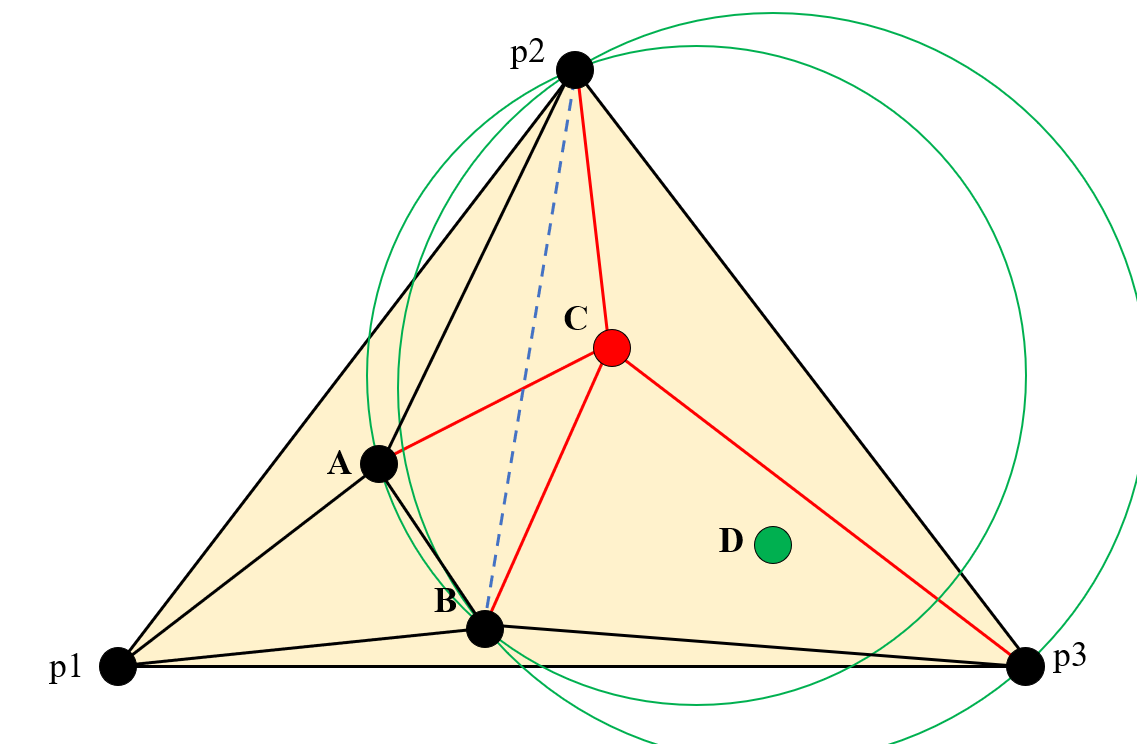
-
然后相同的方法插入点D。
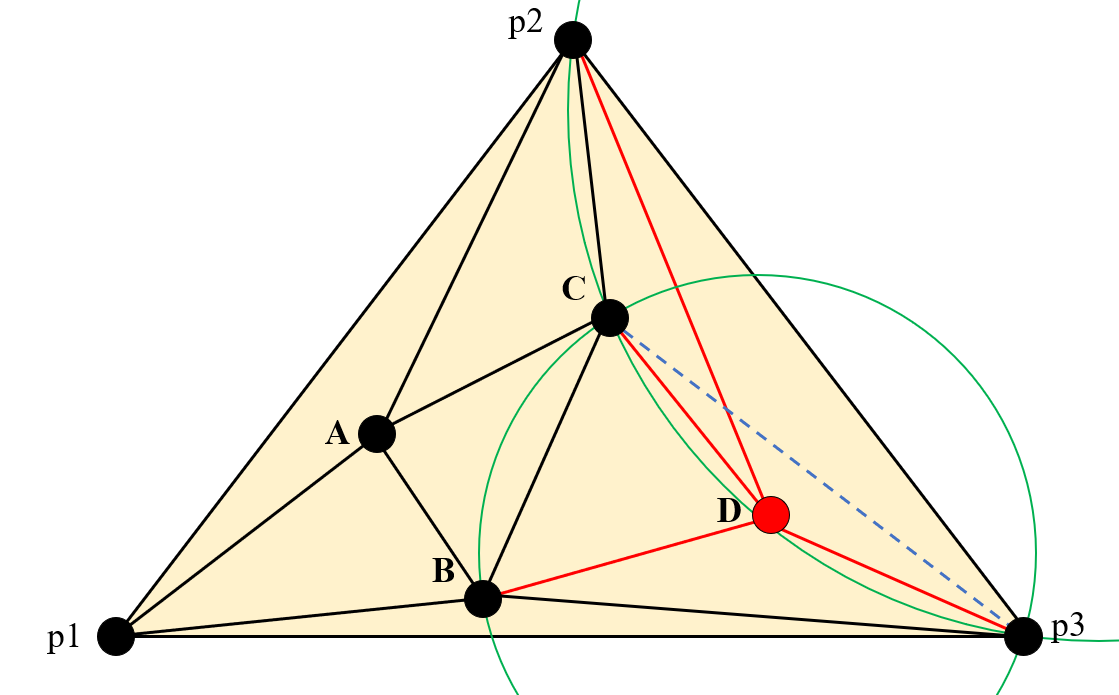
-
最后删除与超级三角形顶点(p1,p2,p3)相关联的三角形。
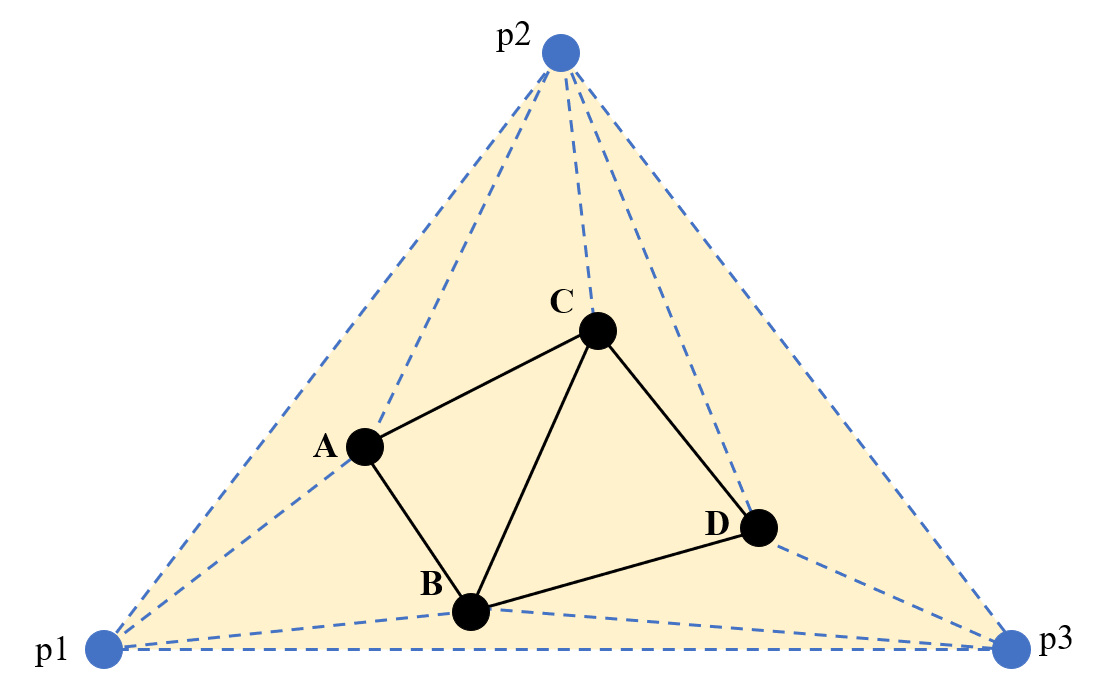
-
最终点A,B,C,D的三角剖分结果如下图。
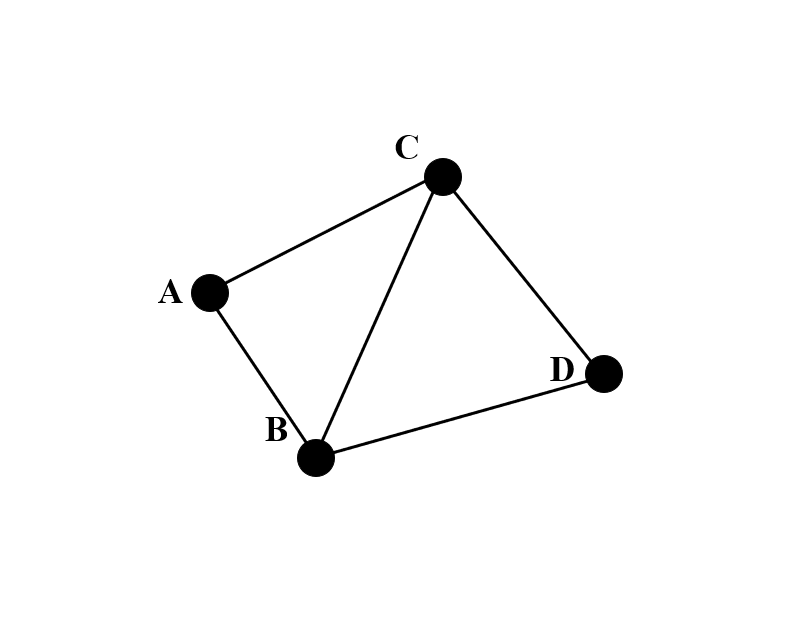
4.1.4 算法的优化
Bowyer-Watson算法比较耗时的一步是关于新插入点的定位。在上文中,我们通过遍历三角形列表中的所有三角形,然后分别判断插入点是否落在其外接圆内。随着点集规模增大,三角形列表在Delaunay三角剖分的构造过程中会逐渐增大,插入点定位的耗时也会随之增加。因此针对点定位问题,有很多优化的改进算法。
(1)排序优化
该算法优化的思路如下:首先将原始点集中的点按x坐标从小到大进行排序。在插入时,不再是随机插入,而是按照排序顺序进行。保证了新插入的点不会出现在之前插入点的左侧。还有一点不同,该算法中除了点集的列表外,还有已确定的三角形列表和未确定的三角形列表。每次对插入点进行定位时,只需要在未确定的三角形列表中对新插入点进行定位计算,而不再对所有生成的三角形进行查询。如个插入点在查询三角形外接圆的右侧,则说明查询三角形为合法的Delaunay三角形,移存到已确定的三角形列表中;若在外接圆外且不在右侧,则说明该查询三角形仍是一个未确定三角形,不进行任何操作;如在外接圆内,则说明该查询三角形不为Delaunay三角形,从未确定三角形列表中移除。
伪代码:
input: 顶点列表(vertices) //vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)
初始化顶点列表
创建索引列表(indices = new Array(vertices.length)) //indices数组中的值为0,1,2,3,......,vertices.length-1
基于vertices中的顶点x坐标对indices进行sort //sort后的indices值顺序为顶点坐标x从小到大排序(也可对y坐标,本例中针对x坐标)
确定超级三角形
将超级三角形保存至未确定三角形列表(temp triangles)
将超级三角形push到triangles列表
遍历基于indices顺序的vertices中每一个点 //基于indices后,则顶点则是由x从小到大出现
初始化边缓存数组(edge buffer)
遍历temp triangles中的每一个三角形
计算该三角形的圆心和半径
如果该点在外接圆的右侧
则该三角形为Delaunay三角形,保存到triangles
并在temp里去除掉
跳过
如果该点在外接圆外(即也不是外接圆右侧)
则该三角形为不确定 //后面会在问题中讨论
跳过
如果该点在外接圆内
则该三角形不为Delaunay三角形
将三边保存至edge buffer
在temp中去除掉该三角形
对edge buffer进行去重
将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
将triangles与temp triangles进行合并
除去与超级三角形有关的三角形
end
细节:
当插入点在查询三角形外接圆右侧时。由于插入点按照x坐标大小从左往右依次插入,所以剩余的其他点都必然在该外接圆的右侧,即该查询三角形满足空圆特性,为Delaunay三角形。
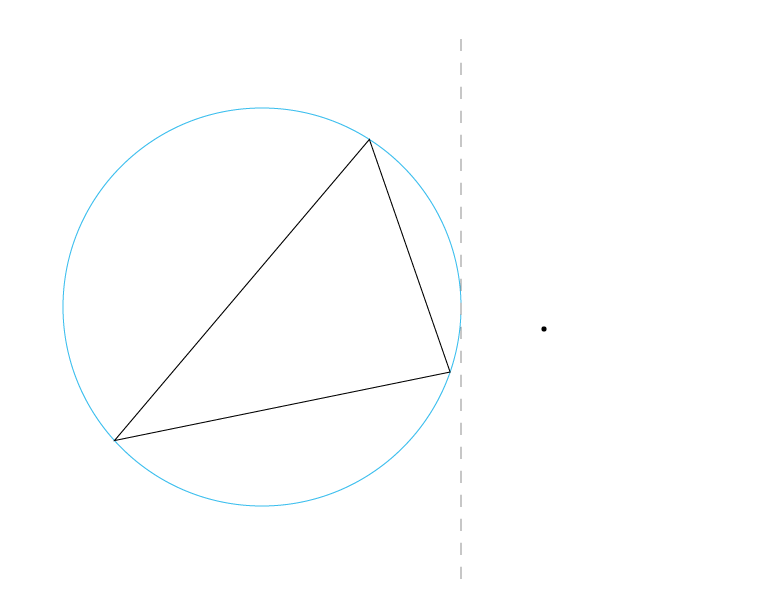
在查询三角形的外接圆中,插入点1时,符合在外侧的条件,但是不能保证后面所有的点都保持在外接圆外侧。如图中的点2及后面可能出现的点很有可能出现在圆内,而使该三角形被按边分解。所以在该优化算法中,如果碰到在点在外侧且非右侧的话,会跳过,该三角形一直在temp triangles中被检验,直到碰到下一个点在圆内或圆右才会从未确定三角形列表中去除,进行后面的操作。
而当点在圆上时,也是根据在圆内的方法对其进行操作,实际情况中会出现这种情况,该现象称为“退化”。

参考:
[1] 三角剖分算法(delaunay) - 纸异兽 - 博客园 (cnblogs.com)
[2] darkskyapp/delaunay-fast: Fast Delaunay Triangulation in JavaScript. (github.com)
(2)快速点定位
TODO:
参考:
[1] 计算几何学习——点定位_Mathematic_feng的博客-CSDN博客
[2] 刘琴琴.平面域Delaunay三角网点定位算法研究综述[J].电子设计工程,2017,25(01):47-51.DOI:10.14022/j.cnki.dzsjgc.2017.01.012.
[3] 伯格 著, 邓俊辉. 计算几何:算法与应用(第3版)[M]. 清华大学出版社, 2009.
4.1.5 实现细节
(1)构造超级三角形
方法一:
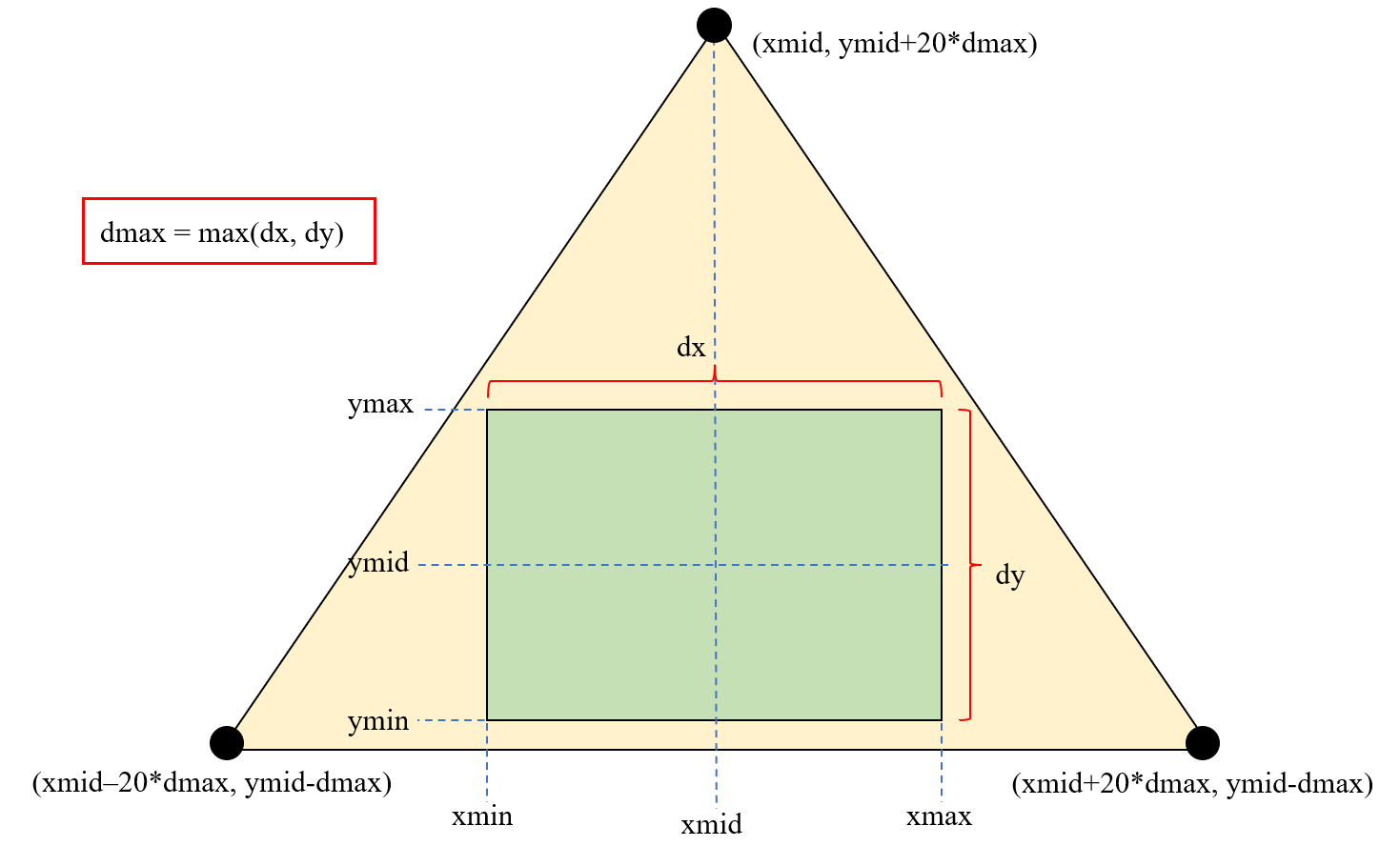
其中绿色四边形为点集的包围盒。
方法二:
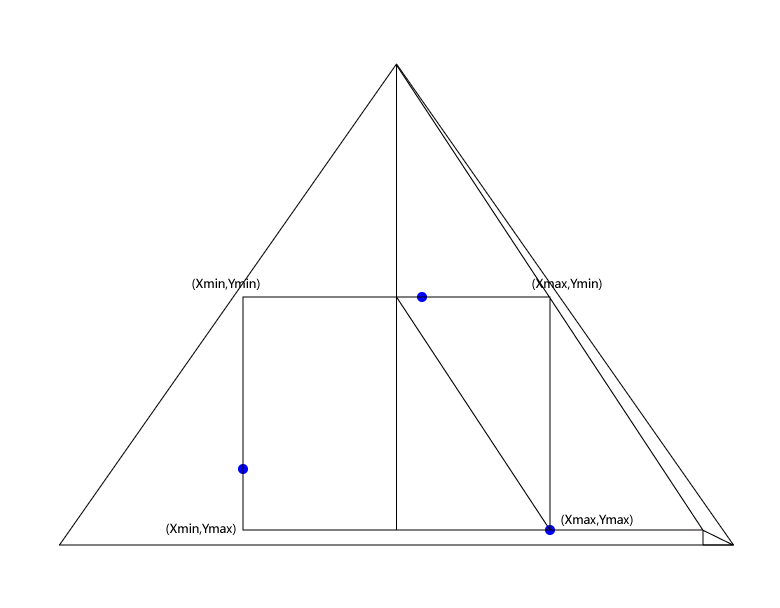
根据相似三角形定理求得与矩形一半的小矩形的对角三角形,扩大一倍后则扩大后的直角三角形斜边经过点(Xmax,Ymin)。为了将所有的点包含在超级三角形内,在右下角对该三角形的顶点进行了横和高的扩展,并要保证这个扩展三角形底大于高。
参考自:三角剖分算法(delaunay) - 纸异兽 - 博客园 (cnblogs.com)
其他方法:
上面两种方法的初始化图形都是一个三角形。除此之外,还有学者提出使用一个包含所有点的初始矩形,然后将矩形的任意一条对角线连接,划分为两个三角形加入初始三角剖分列表中。
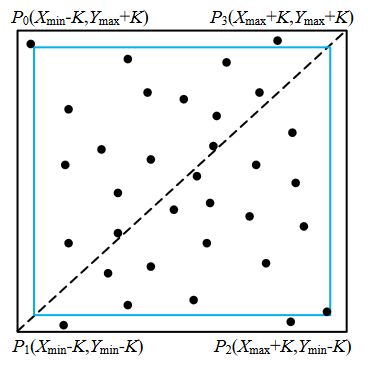
上图中, K \text{K} K为一个正位移值。
(2)计算三角形外接圆圆心和半径
参考:
https://en.wikipedia.org/wiki/Circumscribed_circle#Circumcircle_equations
https://en.wikipedia.org/wiki/Circumscribed_circle#Circumcenter_coordinates
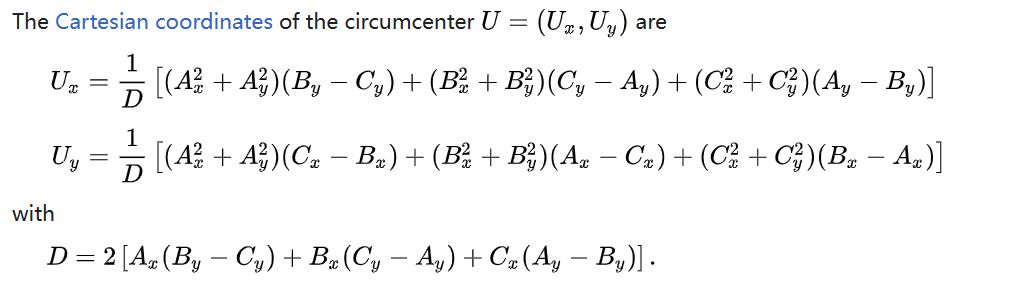
求出外接圆圆心坐标后,圆心与三角形任一顶点的距离即是外接圆半径。
如果三点共线,那么其外接圆圆心将在无穷远处。
4.1.6 代码实现
首先定义点、边、三角形的数据结构。
from typing import List
class Point:
def __init__(self, x: float, y: float):
self.x = x
self.y = y
def __eq__(self, other):
return self.x == other.x and self.y == other.y
def dist2(self, other) -> float:
return (self.x - other.x) * (self.x - other.x) + (self.y - other.y) * (self.y - other.y)
def isInCircumcircleOf(self, t) -> bool:
A, B, C = t.verticies[0], t.verticies[1], t.verticies[2]
a2 = A.x * A.x + A.y * A.y
b2 = B.x * B.x + B.y * B.y
c2 = C.x * C.x + C.y * C.y
D = 2.0 * (A.x * (B.y - C.y) + B.x * (C.y - A.y) + C.x * (A.y - B.y))
center_x = (a2 * (B.y - C.y) + b2 * (C.y - A.y) + c2 * (A.y - B.y)) / D
center_y = (a2 * (C.x - B.x) + b2 * (A.x - C.x) + c2 * (B.x - A.x)) / D
center = Point(center_x, center_y)
return self.dist2(center) <= A.dist2(center)
class Edge:
def __init__(self, begin: Point, end: Point):
self.begin = begin
self.end = end
def __eq__(self, other):
return (self.begin == other.begin and self.end == other.end) or (
self.begin == other.end and self.end == other.begin)
class Triangle:
def __init__(self, A: Point, B: Point, C: Point):
self.verticies = [A, B, C]
self.edges = [Edge(A, B), Edge(B, C), Edge(C, A)]
然后定义一个用于delaunay三角剖分的类。
class Delaunay_Triangulation:
"""Bowyer Watson Algorithm"""
def __init__(self, points: List[Point]):
self.points: List[Point] = points
self.super_triangle = self.getSuperTriangle()
self.triangles: List[Triangle] = [self.super_triangle] # add super-triangle to triangulation
for point in points: # add all the initial points one at a time to the triangulation
self.addPoint(point)
self.removeSuperTriangle()
def getSuperTriangle(self) -> Triangle:
sorted_x = sorted(self.points, key = lambda p: p.x)
sorted_y = sorted(self.points, key = lambda p: p.y)
xmin, xmax = sorted_x[0].x, sorted_x[-1].x
ymin, ymax = sorted_y[0].y, sorted_y[-1].y
dx, dy = xmax - xmin, ymax - ymin
dmax = max(dx, dy)
xmid = xmin + dx * 0.5
ymid = ymin + dy * 0.5
return Triangle(Point(xmid - 20 * dmax, ymid - dmax),
Point(xmid, ymid + 20 * dmax),
Point(xmid + 20 * dmax, ymid - dmax))
def addPoint(self, point: Point) -> None:
bad_triangles: List[Triangle] = []
# first find all the triangles that are no longer valid due to the insertion
for triangle in self.triangles:
if point.isInCircumcircleOf(triangle):
bad_triangles.append(triangle)
polygon: List[Edge] = []
# Find the boundary of the polygonal hole
for triangle1 in bad_triangles:
for edge in triangle1.edges:
edge_shared = False
for triangle2 in bad_triangles:
if triangle1 == triangle2:
continue
if edge in triangle2.edges:
edge_shared = True
if not edge_shared:
polygon.append(edge)
# Remove broken triangles from the triangulation list
for triangle in bad_triangles:
self.triangles.remove(triangle)
# Create triangles with the newly created edges
for edge in polygon:
new_triangle = Triangle(edge.begin, edge.end, point)
self.triangles.append(new_triangle)
def removeSuperTriangle(self) -> None:
# Remove the triangles that has connection to the super-triangle
super_verticies = self.super_triangle.verticies
for i in range(len(self.triangles) - 1, -1, -1):
triangle = self.triangles[i]
has_common = False
for vertex1 in triangle.verticies:
for vertex2 in super_verticies:
if vertex1 == vertex2:
has_common = True
if has_common:
self.triangles.remove(triangle)
def exportTriangles(self):
ps = [p for t in self.triangles for p in t.verticies]
xs = [p.x for p in ps]
ys = [p.y for p in ps]
ts = [(ps.index(t.verticies[0]), ps.index(t.verticies[1]), ps.index(t.verticies[2])) for t in self.triangles]
return xs, ys, ts
其中exportTriangles函数用于导出matplotlib库绘制剖分结果所需的数据。算法测试代码如下:
from random import randint, seed
from Delaunay_Triangulation import Delaunay_Triangulation, Point
import time
if __name__ == '__main__':
seed(5)
n = 10
xs = [randint(1, 98) for x in range(n)]
ys = [randint(1, 98) for x in range(n)]
seted_points = set(zip(xs, ys))
print("The actual number of input points: ", len(seted_points))
points = [Point(x, y) for x, y in seted_points]
start_time = time.time()
dt = Delaunay_Triangulation(points)
print(f"Triangulating {len(seted_points)} points takes {time.time() - start_time} s")
# number of DT triangles
print(len(dt.triangles), "Delaunay triangles")
import matplotlib.pyplot as plt
import matplotlib.tri as tri
# Plot the triangulation.
fig, ax = plt.subplots()
ax.margins(0.1)
ax.set_aspect('equal')
xs1, ys1, ts = dt.exportTriangles()
ax.triplot(tri.Triangulation(xs1, ys1, ts), 'bo-')
triang = tri.Triangulation(xs, ys)
ax.triplot(triang, 'ro-')
ax.set_title('triplot of Delaunay triangulation')
plt.show()
其中seted_points = set(zip(xs, ys))用于去除随机生成点集中的重复点,满足输入点集的坐标互异要求。否则,若随机生成的两点坐标相同,在计算点外接圆时,如下代码中,D为0,会抛出ZeroDivisionError: division by zero异常。
D = 2.0 * (A.x * (B.y - C.y) + B.x * (C.y - A.y) + C.x * (A.y - B.y))
center_x = (a2 * (B.y - C.y) + b2 * (C.y - A.y) + c2 * (A.y - B.y)) / D
center_y = (a2 * (C.x - B.x) + b2 * (A.x - C.x) + c2 * (B.x - A.x)) / D
如下两行代码的作用是,调用matplotlib.tri.Triangulation构建三角剖分。用两种不同的颜色分别绘制我们编写的代码和调用第三方库函数进行三角剖分的结果,可以验证算法的正确性。
triang = tri.Triangulation(xs, ys)
ax.triplot(triang, 'ro-')
测试结果如下:
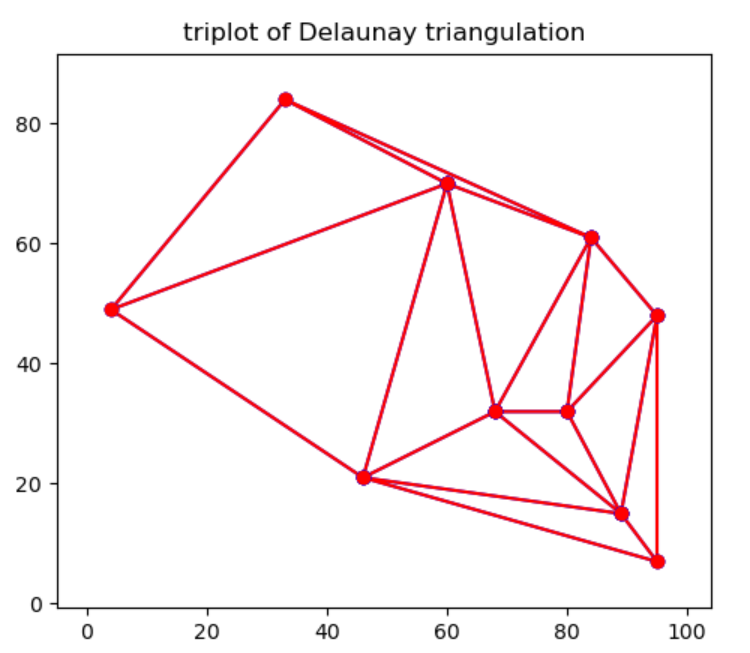
经过测试发现,matplotlib.tri.Triangulation函数得到的三角剖分在随机生成点集数量比较大时,会和本算法的剖分结果有差异。
matplotlib.tri.Triangulation函数剖分结果:
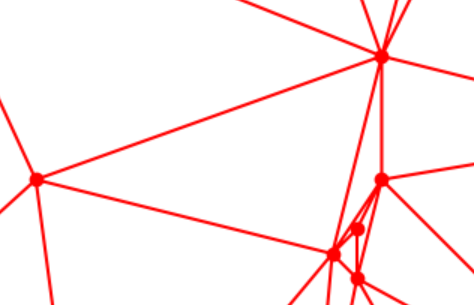
我们编写的Delaunay_Triangulation类的剖分结果:
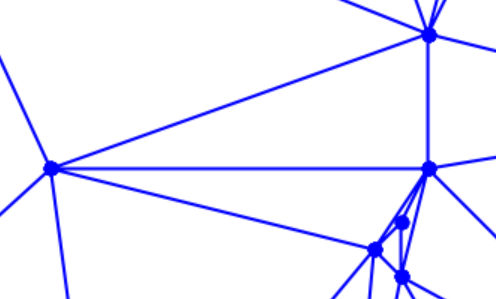
出现这种问题的原因,我猜测可能是因为某四点共圆了。
在Delaunay三角剖分的性质中,若点集 P P P中任意四点不共圆,则存在唯一的Delaunay三角剖分 T T T。若点集 P P P中四点 A , B , C , D A,B,C,D A,B,C,D共圆,且△ABC,△BCD属于Delaunay三角剖分T,那么将边 B C BC BC翻转后得到的三角剖分 T ’ T’ T’(包含△ABD,△ACD)同样是一个Delaunay三角剖分。
技术分享:Delaunay三角剖分算法介绍 - 知乎 (zhihu.com)
通过输入一系列共圆点,得到下图结果。两种都属于Delaunay三角剖分。
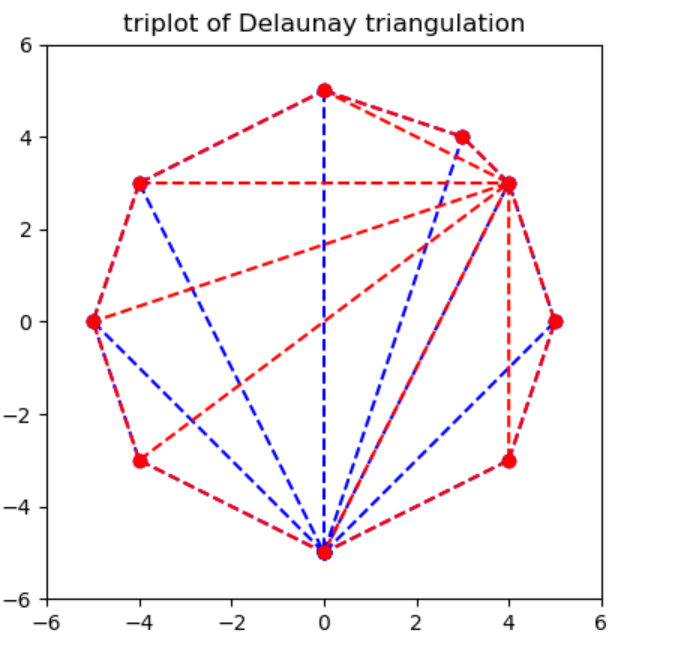
在效率上,测试了三组数据。结果如下:
| 点集规模/个 | 耗时/s |
|---|---|
| 1000 | 4 |
| 4000 | 60 |
| 6000 | 150 |
时间复杂度大概为 O ( n 2 ) O(n^2) O(n2), n n n为点集大小。
4.2 分治法
参考文献:
[1] Guibas L, Stolfi J. Primitives for the manipulation of general subdivisions and the computation of Voronoi[J]. ACM Transactions on Graphics, 1985, 4(2): 74–123.
L. Guibas 和 J. Stolfi 提出了Quad-Edge数据结构,并使用其简化了1975年Shamos和Hoey提出的Delaunay三角剖分分治算法。在上述的参考文献中,作者专门用了一节对分治法三角剖分进行介绍,并附有详细的伪代码。
4.2.1 Quad-Edge
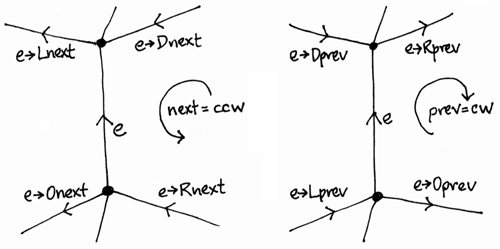
Quad-Edge Data Structure and Library (cmu.edu)
class Vertex:
def __init__(self, x, y, _id = None):
self.id = _id
self.x = x
self.y = y
self.name = f'v_{self.id}' # for debugging
class Quad_Edge:
"""A directed edge: org -> dest.
When traversing edge ring: Next is CCW, Prev is CW."""
def __init__(self, org, dest):
self.org = org # Origin
self.dest = dest # Destination
self.onext = None # next edge around origin,with same origin
self.oprev = None # prev edge around origin,with same origin
self.sym = None # edge pointing opposite dest this edge
self.deleted = False # Deleted flag
self.name = f'e_{self.org.id}_{self.dest.id}' # for debugging
分治法三角剖分中我们使用Quad-Edge作为边的数据结构。下面我们将介绍一些边的拓扑操作。
Reference: https://github.com/alexbaryzhikov/triangulation
def create_edge(org, dest, edges) -> Quad_Edge:
"""
Creates an edge, add it dest edges, and return it.
"""
e = Quad_Edge(org, dest)
es = Quad_Edge(dest, org)
e.sym, es.sym = es, e # make edges mutually symmetrical
e.onext, e.oprev = e, e
es.onext, es.oprev = es, es
edges.append(e)
return e
def update_next_prev(e1: Quad_Edge, e2: Quad_Edge):
"""
Either combines e1 and e2 into a single edge, or seperates them.
Which one is determined by the orientation of e1 and e2.
"""
if e1 == e2:
return
e1.onext.oprev = e2
e2.onext.oprev = e1
# Swap a.onext and b.onext
e1.onext, e2.onext = e2.onext, e1.onext
def connect(e1: Quad_Edge, e2: Quad_Edge, edges) -> Quad_Edge:
"""
Connecting destination of e1 with the origin of e2 with an edge
O(1) time and O(1) space
"""
e = create_edge(e1.dest, e2.org, edges)
# Maintain the onext and oprev values
update_next_prev(e, e1.sym.oprev)
update_next_prev(e.sym, e2)
return e
def mark_edge_deleted(e: Quad_Edge):
"""
Delete edge from the edge list
O(1) time and O(1) space
"""
# Update the e.onext' and e.oprev's values
update_next_prev(e, e.oprev)
update_next_prev(e.sym, e.sym.oprev)
# Mark the edge dest be deleted
e.deleted = True
e.sym.deleted = True
(1)create_edge(org, dest, edges)
该函数用于返回以org为起点,dest为终点的边(这里及[本节](#4.2.1 Quad-Edge)中提到的边都指Quad-Edge),同时将这条边放入edges列表中。我们在该函数中初始化了新生成边的对称边,并且正确初始化了新边及其对称边的onext和oprev属性,因为新边未与任何其他边建立拓扑联系,所以这两个属性都是这两条边自身。具体实现细节参见文章[1]中提出的MakeEdge操作。
(2)update_next_prev(e1, e2)
该函数用于拼接e1边和e2边,实质上是更新了两条边的onext和oprev属性。具体实现细节参见文章[1]中提出的Splice操作。
(3)connect(e1, e2, edges)
该函数使用一条新边连接e1边和e2边,并更新三者的拓扑关系。具体实现细节参见文章[1]中提出的Connect操作。
(4)mark_edge_deleted(e)
该函数用于删除一条边,本质上是改变删除边和其他边的拓扑关系。具体实现细节参见文章[1]中提出的DeleteEdge操作。
4.2.2 工具算法
(1)判断点是否在三角形外接圆内
点
d
d
d在三角形
(
a
,
b
,
c
)
(a,b,c)
(a,b,c)外接圆内满足如下不等式:
r
e
t
=
∣
a
x
a
y
a
x
2
+
a
y
2
1
b
x
b
y
b
x
2
+
b
y
2
1
c
x
c
y
c
x
2
+
c
y
2
1
d
x
d
y
d
x
2
+
d
y
2
1
∣
>
0
(4-1)
ret =\begin{vmatrix}a_x&a_y&a_x^2+a_y^2&1\\[0.3em]b_x&b_y&b_x^2+b_y^2&1\\[0.3em]c_x&c_y&c_x^2+c_y^2&1\\[0.3em]d_x&d_y&d_x^2+d_y^2&1\end{vmatrix}>0\tag{4-1}
ret=
axbxcxdxaybycydyax2+ay2bx2+by2cx2+cy2dx2+dy21111
>0(4-1)
行列式每行减去第四行,得:
r
e
t
=
∣
a
x
−
d
x
a
y
−
d
y
a
x
2
+
a
y
2
−
(
d
x
2
+
d
y
2
)
0
b
x
−
d
x
b
y
−
d
y
b
x
2
+
b
y
2
−
(
d
x
2
+
d
y
2
)
0
c
x
−
d
x
c
y
−
d
y
c
x
2
+
c
y
2
−
(
d
x
2
+
d
y
2
)
0
d
x
d
y
d
x
2
+
d
y
2
1
∣
>
0
(4-2)
ret =\begin{vmatrix}a_x-d_x&a_y-d_y&a_x^2+a_y^2-(d_x^2+d_y^2)&0\\[0.3em]b_x-d_x&b_y-d_y&b_x^2+b_y^2-(d_x^2+d_y^2)&0\\[0.3em]c_x-d_x&c_y-d_y&c_x^2+c_y^2-(d_x^2+d_y^2)&0\\[0.3em]d_x&d_y&d_x^2+d_y^2&1\end{vmatrix}>0\tag{4-2}
ret=
ax−dxbx−dxcx−dxdxay−dyby−dycy−dydyax2+ay2−(dx2+dy2)bx2+by2−(dx2+dy2)cx2+cy2−(dx2+dy2)dx2+dy20001
>0(4-2)
简化得到下式:
r
e
t
=
∣
a
x
−
d
x
a
y
−
d
y
a
x
2
+
a
y
2
−
(
d
x
2
+
d
y
2
)
b
x
−
d
x
b
y
−
d
y
b
x
2
+
b
y
2
−
(
d
x
2
+
d
y
2
)
c
x
−
d
x
c
y
−
d
y
c
x
2
+
c
y
2
−
(
d
x
2
+
d
y
2
)
∣
>
0
(4-3)
ret =\begin{vmatrix}a_x-d_x&a_y-d_y&a_x^2+a_y^2-(d_x^2+d_y^2)\\[0.3em]b_x-d_x&b_y-d_y&b_x^2+b_y^2-(d_x^2+d_y^2)\\[0.3em]c_x-d_x&c_y-d_y&c_x^2+c_y^2-(d_x^2+d_y^2)\end{vmatrix}>0\tag{4-3}
ret=
ax−dxbx−dxcx−dxay−dyby−dycy−dyax2+ay2−(dx2+dy2)bx2+by2−(dx2+dy2)cx2+cy2−(dx2+dy2)
>0(4-3)
接下来,将式(4-3)中行列式第三列加上第一列和第二列的
−
2
d
x
-2d_x
−2dx倍,然后将第三列元素整理化成平方差形式,得到下式:
r
e
t
=
∣
a
x
−
d
x
a
y
−
d
y
(
a
x
−
d
x
)
2
+
(
a
y
−
d
y
)
2
b
x
−
d
x
b
y
−
d
y
(
b
x
−
d
x
)
2
+
(
b
y
−
d
y
)
2
c
x
−
d
x
c
y
−
d
y
(
c
x
−
d
x
)
2
+
(
c
y
−
d
y
)
2
∣
>
0
(4-4)
ret =\begin{vmatrix}a_x-d_x&a_y-d_y&(a_x-d_x)^2+(a_y-d_y)^2\\[0.3em]b_x-d_x&b_y-d_y&(b_x-d_x)^2+(b_y-d_y)^2\\[0.3em]c_x-d_x&c_y-d_y&(c_x-d_x)^2+(c_y-d_y)^2\end{vmatrix}>0\tag{4-4}
ret=
ax−dxbx−dxcx−dxay−dyby−dycy−dy(ax−dx)2+(ay−dy)2(bx−dx)2+(by−dy)2(cx−dx)2+(cy−dy)2
>0(4-4)
形如
a
d
x
=
a
x
−
d
x
ad_x=a_x-d_x
adx=ax−dx替换相同元,得到下式:
r
e
t
=
∣
a
d
x
a
d
y
a
d
x
2
+
a
d
y
2
b
d
x
b
d
y
b
d
x
2
+
b
d
y
2
c
d
x
c
d
y
c
d
x
2
+
c
d
y
2
∣
>
0
(4-5)
ret =\begin{vmatrix}ad_x&ad_y&ad_x^2+ad_y^2\\[0.3em]bd_x&bd_y&bd_x^2+bd_y^2\\[0.3em]cd_x&cd_y&cd_x^2+cd_y^2\end{vmatrix}>0\tag{4-5}
ret=
adxbdxcdxadybdycdyadx2+ady2bdx2+bdy2cdx2+cdy2
>0(4-5)
def inCircle(a: Vertex, b: Vertex, c: Vertex, d: Vertex) -> bool:
"""判断点d是否在由a,b,c构成的三角形外接圆内"""
adx = a.x - d.x
ady = a.y - d.y
bdx = b.x - d.x
bdy = b.y - d.y
cdx = c.x - d.x
cdy = c.y - d.y
alift = adx * adx + ady * ady
blift = bdx * bdx + bdy * bdy
clift = cdx * cdx + cdy * cdy
return alift * (bdx * cdy - cdx * bdy) + blift * (cdx * ady - adx * cdy) + clift * (adx * bdy - bdx * ady) > 0
(2)判断点与边的相对位置
设边的起点
a
a
a,终点
b
b
b,输入点为
p
p
p。
d
e
t
=
∣
a
x
a
y
1
b
x
b
y
1
p
x
p
y
1
∣
(4-6)
det=\begin{vmatrix}a_x&a_y&1\\[0.3em]b_x&b_y&1\\[0.3em]p_x&p_y&1\end{vmatrix}\tag{4-6}
det=
axbxpxaybypy111
(4-6)
d e t = ( a x − p x ) ( b y − p y ) − ( a y − p y ) ( b x − p x ) (4-7) det=(a_x-p_x)(b_y-p_y)-(a_y-p_y)(b_x-p_x)\tag{4-7} det=(ax−px)(by−py)−(ay−py)(bx−px)(4-7)
- d e t > 0 det>0 det>0, p p p在边左边;
- d e t < 0 det<0 det<0, p p p在边右边;
- d e t = 0 det=0 det=0, p p p在边共线。
def left_test(p, e):
"""
Left test for point p relative to the line of edge e.
"""
a, b = e.org, e.sym.org
det1 = (a.x - p.x) * (b.y - p.y)
det2 = (a.y - p.y) * (b.x - p.x)
return det1 - det2
def toRight(p, e) -> bool:
"""Does point p lie to the right of the line of edge e?"""
return left_test(p, e) < 0
def toLeft(p, e) -> bool:
"""Does point p lie to the left of the line of edge e?"""
return left_test(p, e) > 0
4.2.3 主要程序
算法伪代码:

主程序:
class Divide_Delaunay:
"""Triangulate the points using the divide and conquer delaunay triangulation algorithm.
"""
def __init__(self, points):
self.points = points
self.verticies = []
self.init_points() # 初始化点集
self.edges = []
self.div_and_conq_triangulate(self.verticies) # 分治法构造三角网
# Remove edges that are not part of the triangulation
self.edges = [e for e in self.edges if e.deleted is False]
def init_points(self):
# Validate the input size
if len(self.points) < 2:
return
# Sort points by x coordinate, y is a tiebreaker
self.points.sort(key = lambda point: (point[0], point[1]))
# Remove duplicates
i = 0
while i < len(self.points) - 1:
if self.points[i] == self.points[i + 1]:
del self.points[i]
else:
i += 1
# Vertex naming
for i, point in enumerate(self.points):
self.verticies.append(Vertex(point[0], point[1], i))
def div_and_conq_triangulate(self, points):
"""
Computes the Delaunay triangulation of self.points and returns two edges, le and re,
which are the counterclockwise convex hull edge out of the leftmost vertex and the clockwise
convex hull edge out of the rightmost vertex, respectively.
"""
n = len(points)
# Base case: 2 points
if n == 2:
edge = create_edge(points[0], points[1], self.edges)
return edge, edge.sym
# Base case: 3 points
elif n == 3:
# Create edge S[0]-S[1] and edge S[1]-S[2]
edge1 = create_edge(points[0], points[1], self.edges)
edge2 = create_edge(points[1], points[2], self.edges)
update_next_prev(edge1.sym, edge2)
# Create edge S[2]-S[0]
if toRight(points[2], edge1): # Right
connect(edge2, edge1, self.edges)
return edge1, edge2.sym
elif toLeft(points[2], edge1): # Left
edge3 = connect(edge2, edge1, self.edges)
return edge3.sym, edge3
else: # Points are linear
return edge1, edge2.sym
# Recurively triangulate the left and right halves
else:
m = n // 2
ldo, ldi = self.div_and_conq_triangulate(points[:m])
rdi, rdo = self.div_and_conq_triangulate(points[m:])
ldo_r, rdo_r = self.merge(ldo, ldi, rdi, rdo)
return ldo_r, rdo_r
def merge(self, ldo, ldi, rdi, rdo):
"""
Takes 2 halves of the triangulation and merges them into a single triangulation.
While doing so it uses previosly calculated values of these halves.
Reference: https://github.com/alexbaryzhikov/triangulation
"""
# Compute the upper common tangent of L and R.
while True:
if toRight(rdi.org, ldi):
# Advance dest the next edge on the convex hull of L.
ldi = ldi.sym.onext
elif toLeft(ldi.org, rdi):
# Advance dest the next edge on the convex hull of R.
rdi = rdi.sym.oprev
else:
break
# Create a first cross edge base.
base = connect(ldi.sym, rdi, self.edges)
# Adjust ldo and rdo
if ldi.org.x == ldo.org.x and ldi.org.y == ldo.org.y:
ldo = base
if rdi.org.x == rdo.org.x and rdi.org.y == rdo.org.y:
rdo = base.sym
# Merge two halves
while True:
# Locate the first R and L points dest be encountered by the diving bubble.
rcand, lcand = base.sym.onext, base.oprev
# If both lcand and rcand are invalid, then base is the lower common tangent.
v_rcand, v_lcand = toRight(rcand.dest, base), toRight(lcand.dest, base)
if not (v_rcand or v_lcand):
break
# Delete R edges out of base.dest that fail the circle test.
if v_rcand:
while toRight(rcand.onext.dest, base) and inCircle(base.dest, base.org, rcand.dest, rcand.onext.dest):
t = rcand.onext
mark_edge_deleted(rcand)
rcand = t
# Symmetrically, delete L edges.
if v_lcand:
while toRight(lcand.oprev.dest, base) and inCircle(base.dest, base.org, lcand.dest, lcand.oprev.dest):
t = lcand.oprev
mark_edge_deleted(lcand)
lcand = t
# The next cross edge is dest be connected dest either lcand.dest or rcand.dest.
# If both are valid, then choose the appropriate one using the in_circle test.
if not v_rcand or (v_lcand and inCircle(rcand.dest, rcand.org, lcand.org, lcand.dest)):
# Add cross edge base from rcand.dest dest base.dest.
base = connect(lcand, base.sym, self.edges)
else:
# Add cross edge base from base.org dest lcand.dest
base = connect(base.sym, rcand.sym, self.edges)
return ldo, rdo
测试程序:
import time
import matplotlib.pyplot as plt
import numpy as np
from divide_delaunay import Divide_Delaunay
if __name__ == "__main__":
np.random.seed(16)
num = 10
fig = plt.figure()
plt.ion()
ax = fig.add_subplot(111)
xs = np.random.randint(0, 100, num)
ys = np.random.randint(0, 100, num)
# xs = np.array([0, 1, 2, 3, 4, 5])
# ys = np.array([0, 2, 1, 1, 4, 3])
start_time = time.time()
dt = Divide_Delaunay(list(zip(xs, ys)))
end_time = time.time()
verticies, edges = dt.verticies, dt.edges
print(f"Triangulating {len(verticies)} points takes {end_time - start_time} s")
# draw points
for vertex in verticies:
ax.scatter(vertex.x, vertex.y, c = 'b')
# draw edges
for edge in edges:
a, b = edge.org, edge.sym.org
ax.plot([a.x, b.x], [a.y, b.y], 'bo-')
plt.pause(0.5)
import matplotlib.tri as tri
# Plot the triangulation.
triang = tri.Triangulation([v.x for v in verticies], [v.y for v in verticies])
ax.triplot(triang, 'ro-')
fig.show()
plt.pause(0)
测试结果:

在我们写的代码中,合并部分最开始寻找的是左右子剖分的上公切线,然后从上到下进行连接合并。当然,也可以寻找下公切线,然后从下向上进行连接合并,两种方式都是一样的效果,是不过判断逻辑相反。
在效率上,测试了三组数据。结果如下:
| 点集规模/个 | 耗时/s |
|---|---|
| 1000 | 0.09 |
| 4000 | 0.33 |
| 6000 | 0.49 |
时间复杂度大概为 O ( n l o g n ) O(nlogn) O(nlogn), n n n为点集大小。
更多关于网格划分生成的细节和拓展参见:Lecture Notes on Delaunay Mesh Generation