零基础小白共计花费2小时38分04秒完成对小波的“平地起高楼”学习。
记录所有学习过程。
一、大致浏览PPT
这个阶段跳着看,太难的跳过
1.总结知识点
共四个部分
1.小波介绍
2.小波变换
- 小波变换的定义
- 连续小波变换的定义
- 离散小波变换
- 小波重构
3.哈尔小波变换
- 哈尔小波基函数
- 一维哈尔小波变换
- 规范化方法
4.二维哈尔小波变换
- 例子
- 方法
2.第一遍浏览PPT(记录重点内容)
2.1第一部分 小波介绍
小波理论之父:伊夫·梅尔(Yves Meyer)
奠定小波理论的时代:1980年代
2.2第二部分 小波变换
2.2.1小波变换(WT)
小波对函数在空间和时间上进行局部化分析的数学变换
思考历程:
什么是小波?
百度之后发现需要先理解傅里叶变换的概念(虽然学过但全忘光了。)
百度“傅里叶变换”
学习资料:
B站首发!草履虫都能看懂的【傅里叶变换】讲解,清华大学李永乐老师教你如何理解傅里叶变换
傅里叶分析之掐死教程(完整版)更新于2014.06.06
【通过以上资料了解基础概念,补充几点:
1.基函数是函数空间中的基本元素,函数空间中的每个连续函数都可表示为基函数的线性组合】
2.在傅里叶变换中,一个函数可用频率不同的正弦波之和表示,这些正弦波称为傅里叶变换的基函数—————————————————————————————————————————————
重新回到小波
为什么要用小波?因为傅里叶变换有缺陷“傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
PPT中总结傅里叶变换的缺点为:
a.只有频率分辨率,没有时间分辨率
b.可以确定信号中包含哪些频率的信号,但不能确定具有这些频率的信号出现在什么时候”
小波的做法是“小波把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了”
以上关于小波的内容选自 形象易懂讲解算法I——小波变换 具体可看这片文章
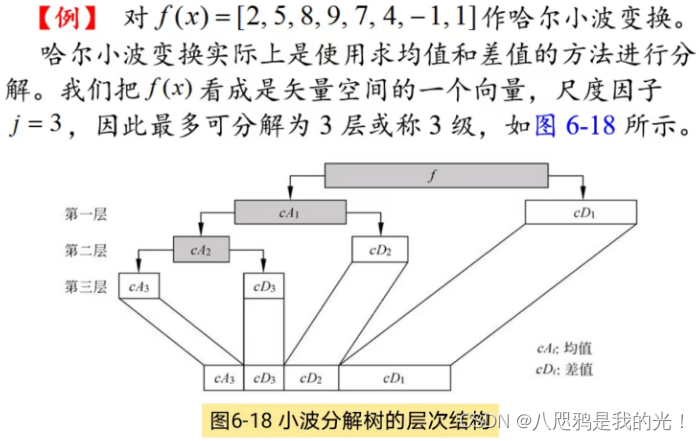
2.2.2连续小波变换(CWT)【以下皆为PPT内容】
连续小波指没有经过数字化的小波
小波分析把一个信号分解成一系列小波之和,这些小波是母小波经过移位和缩放之后的小波,可以用作表示函数的基函数。
凡能用傅里叶分析的函数都可用小波分析。
用不规则的小波分析变化激烈的信号比用平滑的正弦波更有效,对信号的基本特性描述地更准确。
CWT的变换过程:

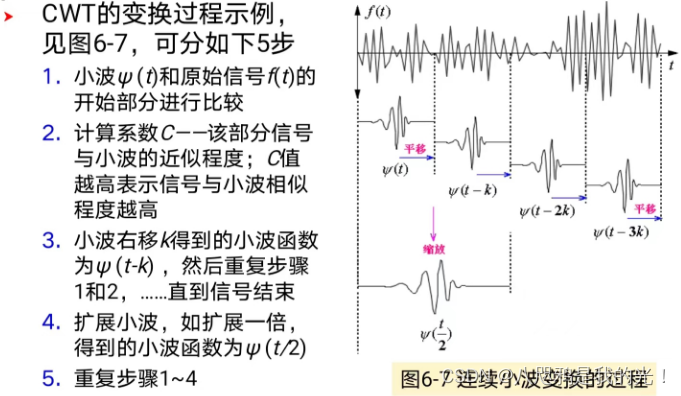
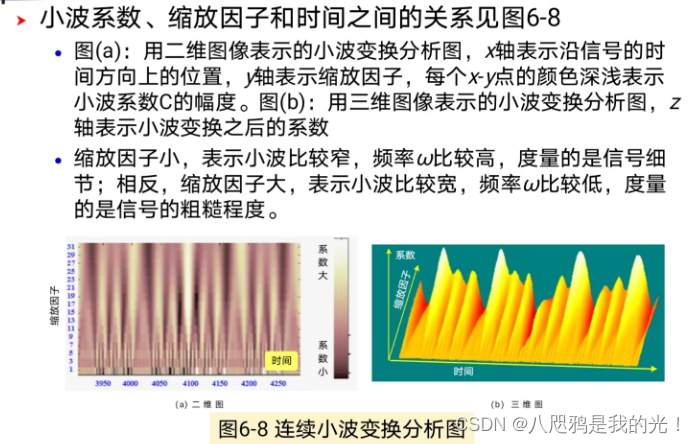
2.2.3小波基函数
一个函数可以用小波基函数的线性组合表示
小波:由定义在有限区间里具有基本形状的函数构造的小波
母小波:构造小波的函数
子小波:母小波函数构造的小波
小波基函数:通过缩放和平移母小波构造的一系列小波函数

2.2.4 离散小波变换(DWT)
定义
概念:使用离散小波的小波变换
离散小波:连续小波采样和量化后的小波
2.2.5 小波重构(IDWT)
概念:把分解的系数还原成原始信号的过程称为小波重构或合成
在数学上称为逆离散小波变换(IDWT)
2.3 第三部分 哈尔小波变换
2.3.1 哈尔小波基函数
哈尔小波是小波中最简单的小波

2.3.2 一维哈尔小波变换
学习思路:完全看不懂概念,直接看题
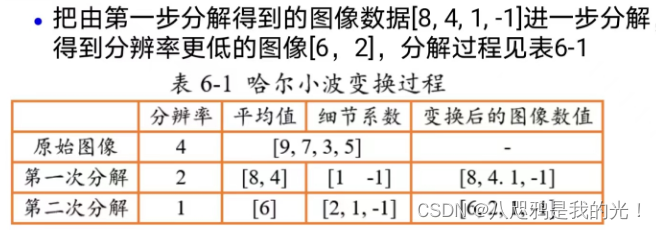
例题:假设只有4个像素的一维图像,对应图像位置的像素值分别为[9,7,3,5],即x1=9 x2=7 x3=3 x4=5,计算一维离散哈尔小波变换的系数
答:第一步:求均值
平均值就是相邻一对像素的平均值
分为两对,第一对平均值为(9+7)/2=8 第二对(3+5)/2=4
存储像素的均值为[8,4]
变换后的图像分辨率为原图像1/2
第二步:求差值
差值就是相邻一对像素的差值的平均值
第一对像素的细节系数:(9-7)/2=1,第二对为-1
存储像素的细节系数为[1,-1]
原始图像数据[9,7,3,5]变换为[8,4,1,-1]
重构图像时解下面的方程组
第三步:重复第一步和第二步
看完例子还是一头雾水,但掌握了一维哈尔小波变换的步骤。可以回头去看定义了。
好吧,PPT的定义很抽象,百度之。
Haar 小波——原理
看完后发现还是需要会用啊,不过理解之后如何应用能记得牢固些了。
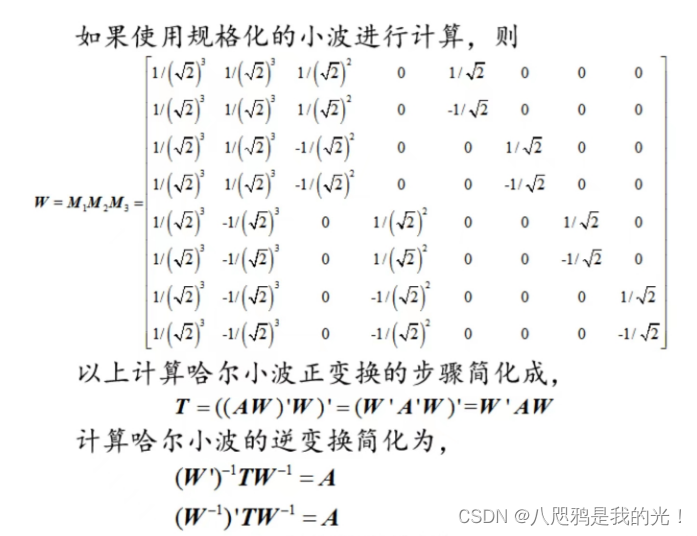
2.3.3 规范化算法
规范化的哈尔小波变换比起非规范化的差别在于规范化的变换中用2½代替2(这是因为要满足小波基函数为正交基的要求,但并不影响对哈尔小波变换的理解。)

上例子:
举一反三嘛,也不难。
2.4 第四部分 二维哈尔小波变换
2.4.1二维小波变换举例



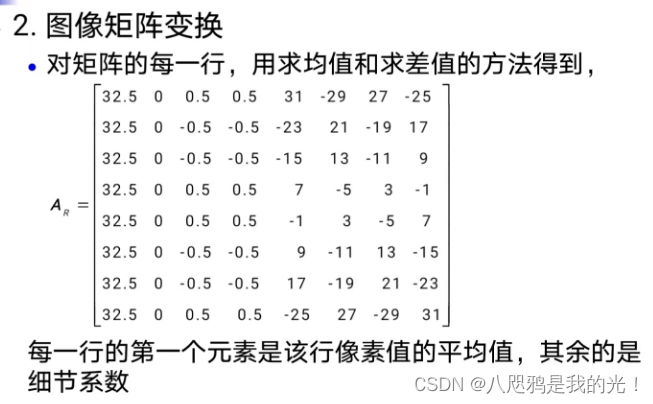
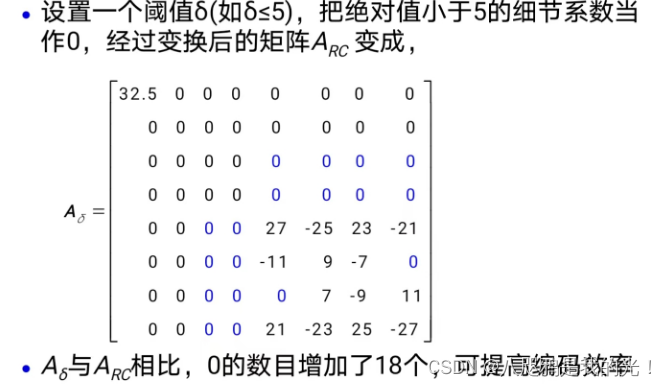
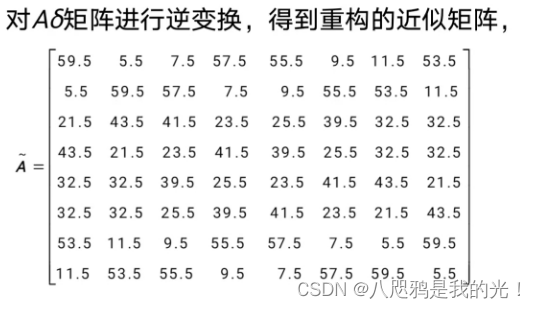
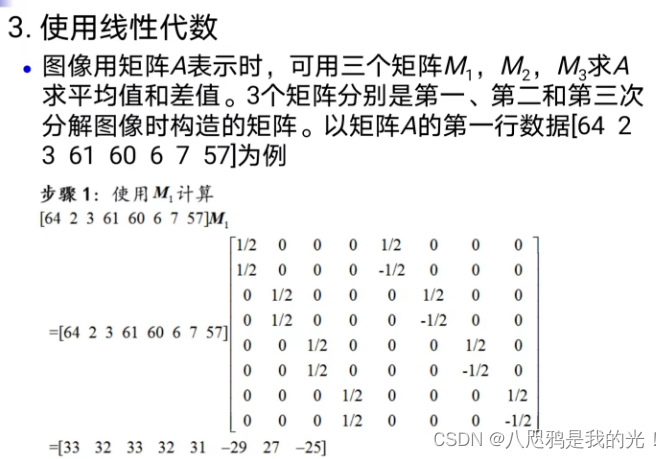
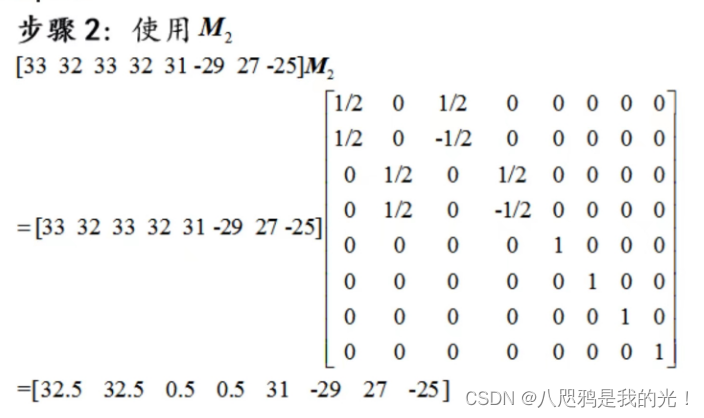

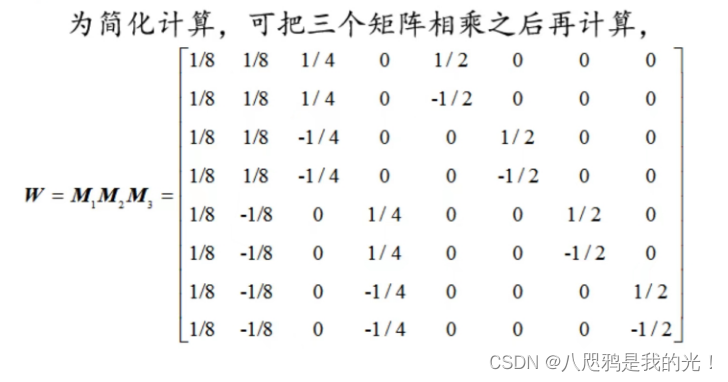
2.4.2二维小波变换方法
- 标准分解
- 非标准分解
这两种方法的变换结果完全相同
非标准分解算法的计算量少
标准分解方法
- 1.使用一维小波对图像每一行的像素值进行变换,产生平均值和细节系数
- 2.使用同样方法对行变换后的图像的列进行变换,产生这幅图像的平均值和细节系数
非标准分解方法
- 用一维小波交替对每行每列的像素值进行变换,变换结果只有1/4的像素包含均值,再对这1/4的均值重复计算行和列像素对的均值和差值,以此类推。
二、回看PPT
这一遍查漏补缺,发现一开始很抽象的文字都能看懂了
第一部分小波介绍
小波是什么?
在有限时间范围内变化且其平均值为0的数学函数
具有有限的持续时间和突变的频率和振幅
在有限的时间范围内,它的平均值=0
小波简史
小波发展史是函数表达方法的发展史
1807年傅里叶揭示一个原理:一个函数可以表示成一系列正弦和余弦函数之和
第二部分 小波变换
这个部分就2.2.4和2.2.5完全看不懂PPT,先暂时不管它了,总复习时再看。
2.2.4 离散小波变换(DWT)
2.2.5 小波重构(IDWT)
总结
共计花费2小时38分04秒完成以上记录和学习。