一、 题目

1. 题目描述

1610. 可见点的最大数目

难度：2147

给你一个点数组 points 和一个表示角度的整数 angle ，你的位置是 location ，其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。

最开始，你面向东方进行观测。你 不能 进行移动改变位置，但可以通过 自转 调整观测角度。换句话说，posx 和 posy 不能改变。你的视野范围的角度用 angle 表示， 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数，那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。

Your browser does not support the video tag or this video format.

对于每个点，如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ，那么你就可以看到它。

同一个坐标上可以有多个点。你所在的位置也可能存在一些点，但不管你的怎么旋转，总是可以看到这些点。同时，点不会阻碍你看到其他点。

返回你能看到的点的最大数目。

示例 1：

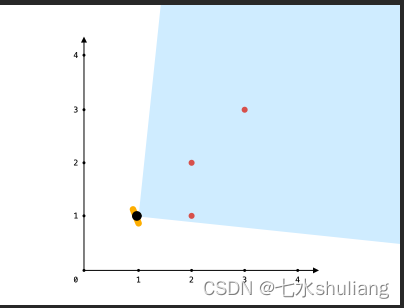
输入：points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出：3
解释：阴影区域代表你的视野。在你的视野中，所有的点都清晰可见，尽管 [2,2] 和 [3,3]在同一条直线上，你仍然可以看到 [3,3] 。

示例 2：

输入：points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出：4
解释：在你的视野中，所有的点都清晰可见，包括你所在位置的那个点。

示例 3：

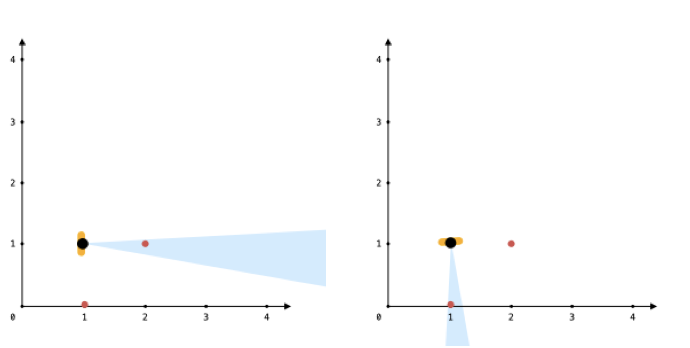
输入：points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出：1
解释：如图所示，你只能看到两点之一。

提示：

• 1 <= points.length <= 105
• points[i].length == 2
• location.length == 2
• 0 <= angle < 360
• 0 <= posx, posy, xi, yi <= 100

2. 原题链接

链接: 1610. 可见点的最大数目

二、 解题报告

1. 思路分析

这是一道纯几何题。
在极坐标系中，平面上任何一点到极点的连线和极轴的夹角叫做极角。

• 把人站的点看做原点，先求出所有点对于目标点的极角。
• 然后排个序，查看目标角度范围内的最大数量。
• 这就变成了一道非常普通的滑窗。
• 求极角两个方式，我们选2:
  • atan(dy,dx):值域[-90,90]，要分别讨论象限
  • atan(dy,dx):值域[-180,180]，直接用。
• 这里由于含从第四象限到第一象限的过度，于是在原极角数组中直接拼接一些+360度的假点，避免分类讨论。
• 注意，位于原点的点一直能看到，且不可求tan，因此单独处理。

---

• 再注意，原题给的angle是度，这里需要*pi/180转化一下。

2. 复杂度分析

排序时间复杂度O(nlog₂n)

3. 代码实现

class Solution:
    def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:
        t = ans = 0
        jiao = []
        a,b = location
        for x,y in points:
            if x == a and y == b:
                t += 1
            else:
                jiao.append(atan2(y-b,x-a))
        jiao.sort()
        jiao.extend([x + 2*pi for x in jiao])
        n = len(jiao)
        q = deque()
        # print(jiao)
        x = angle*pi/180
        for v in jiao:
            q.append(v)
            while q and v - q[0] > x:
                q.popleft()
            ans = max(ans,len(q))
        return ans + t

三、 本题小结

1. 第一次做极角的题。

四、 参考链接