遗传算法(Genetic Algorithm,GA)
是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法。它借用了生物遗传学的观点,通过自然选择、遗传和变异等作用机制,实现各个个体适应性的提高。
基因型 (Genotype)
在自然界中,通过基因型表征繁殖,繁殖和突变,基因型是组成染色体的一组基因的集合。
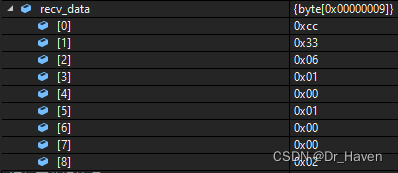
在遗传算法中,每个个体都由代表基因集合的染色体构成。例如,一条染色体可以表示为二进制串,其中每个位代表一个基因:
种群 (Population)
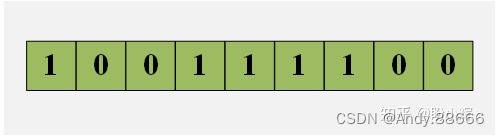
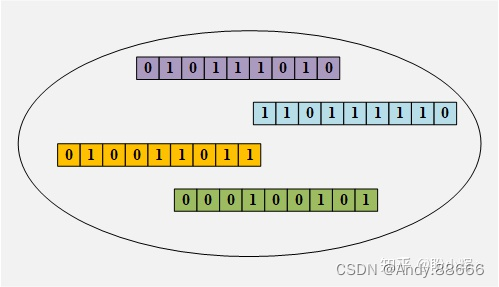
遗传算法保持大量的个体 (individuals) —— 针对当前问题的候选解集合。由于每个个体都由染色体表示,因此这些种族的个体 (individuals) 可以看作是染色体集合:
适应度函数 (Fitness function)
在算法的每次迭代中,使用适应度函数(也称为目标函数)对个体进行评估。目标函数是用于优化的函数或试图解决的问题。
适应度得分更高的个体代表了更好的解,其更有可能被选择繁殖并且其性状会在下一代中得到表现。随着遗传算法的进行,解的质量会提高,适应度会增加,一旦找到具有令人满意的适应度值的解,终止遗传算法。
选择 (Selection)
在计算出种群中每个个体的适应度后,使用选择过程来确定种群中的哪个个体将用于繁殖并产生下一代,具有较高值的个体更有可能被选中,并将其遗传物质传递给下一代。
仍然有机会选择低适应度值的个体,但概率较低。这样,就不会完全摒弃其遗传物质。
交叉 (Crossover)
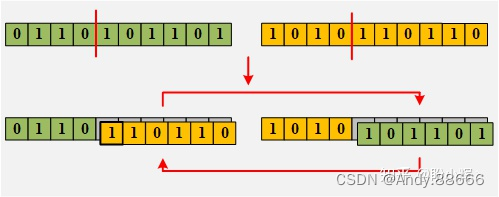
为了创建一对新个体,通常将从当前代中选择的双亲样本的部分染色体互换(交叉),以创建代表后代的两个新染色体。此操作称为交叉或重组:
突变 (Mutation)
突变操作的目的是定期随机更新种群,将新模式引入染色体,并鼓励在解空间的未知区域中进行搜索。
突变可能表现为基因的随机变化。变异是通过随机改变一个或多个染色体值来实现的。例如,翻转二进制串中的一位:

遗传算法理论
构造遗传算法的理论假设——针对当前问题的最佳解是由多个要素组成的,当更多此类要素组合在一起时,将更接近于问题的最优解。
种群中的个体包含一些最优解所需的要素,重复选择和交叉过程将个体将这些要素传达给下一代,同时可能将它们与其他最优解的基本要素结合起来。这将产生遗传压力,从而引导种群中越来越多的个体包含构成最佳解决方案的要素
图式定理 (schema theorem)
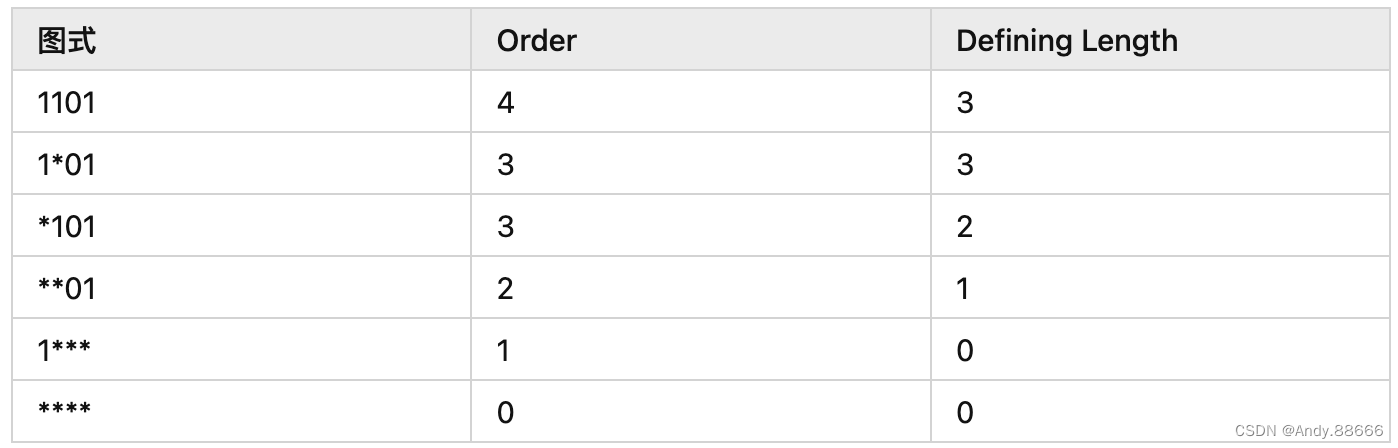
如果一组染色体用长度为 4 的二进制串表示,则图式 1*01 表示所有这些染色体,其中最左边的位置为1,最右边的两个位置为01,从左边数的第二个位置为 1 或 0,其中 * 表示通配符。
对于每个图式,具有以下两个度量:
阶 (Order):固定数字的数量
定义长度 (Defining length):最远的两个固定数字之间的距离
下表提供了四位二进制图式及其度量的几个示例:
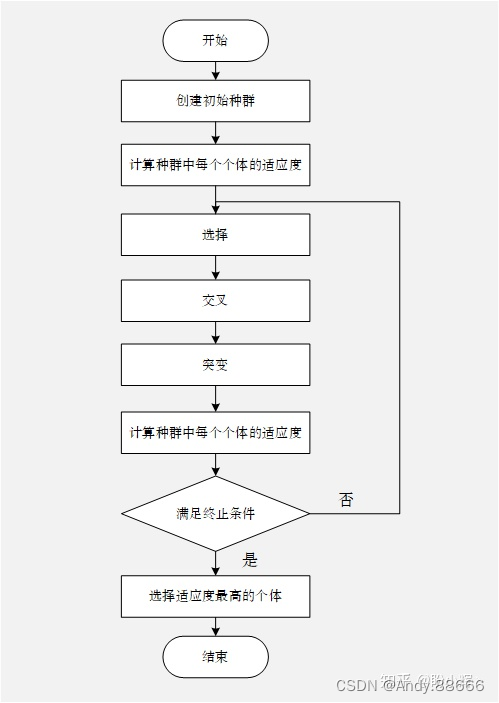
遗传算法的组成要素
遗传算法的核心是循环——依次应用选择,交叉和突变的遗传算子,然后对个体进行重新评估——一直持续到满足停止条件为止
精英主义 (elitism)
尽管遗传算法群体的平均适应度通常随着世代的增加而增加,但在任何时候都有可能失去当代的最佳个体。这是由于选择、交叉和变异运算符在创建下一代的过程中改变了个体。在许多情况下,丢失是暂时的,因为这些个体(或更好的个体)将在下一代中重新引入种群。
但是,如果要保证最优秀的个体总是能进入下一代,则可以选用精英主义策略。这意味着,在我们使用通过选择、交叉和突变创建的后代填充种群之前,将前 n 个个体( n 是预定义参数)复制到下一代。复制后的的精英个体仍然有资格参加选择过程,因此仍可以用作新个体的亲本。
Elitism 策略有时会对算法的性能产生重大的积极影响,因为它避免了重新发现遗传过程中丢失的良好解决方案所需的潜在时间浪费。