文章目录
- 前言
- Nodejs在vscode中的配置
- 1、扩展插件
- Code Runner
- JavaScript(ES6) code snippet
- Live Server
- 2、创建配置文件
- 3、调整配置文件内容
前言
npm ERR! enoent This is related to npm not being able to find a file.
‘vue-cli-service’ 不是内部或外部命令,也不是可运行的程序
今天在使用vscode开发前端项目的时候,报错如上所示,提示了npm无法使用!
之前我们总结过windows下通过nvm安装切换nodejs,这里就不再赘述,这里主要将vscode中如何配置node来配置一下
Nodejs在vscode中的配置
1、扩展插件
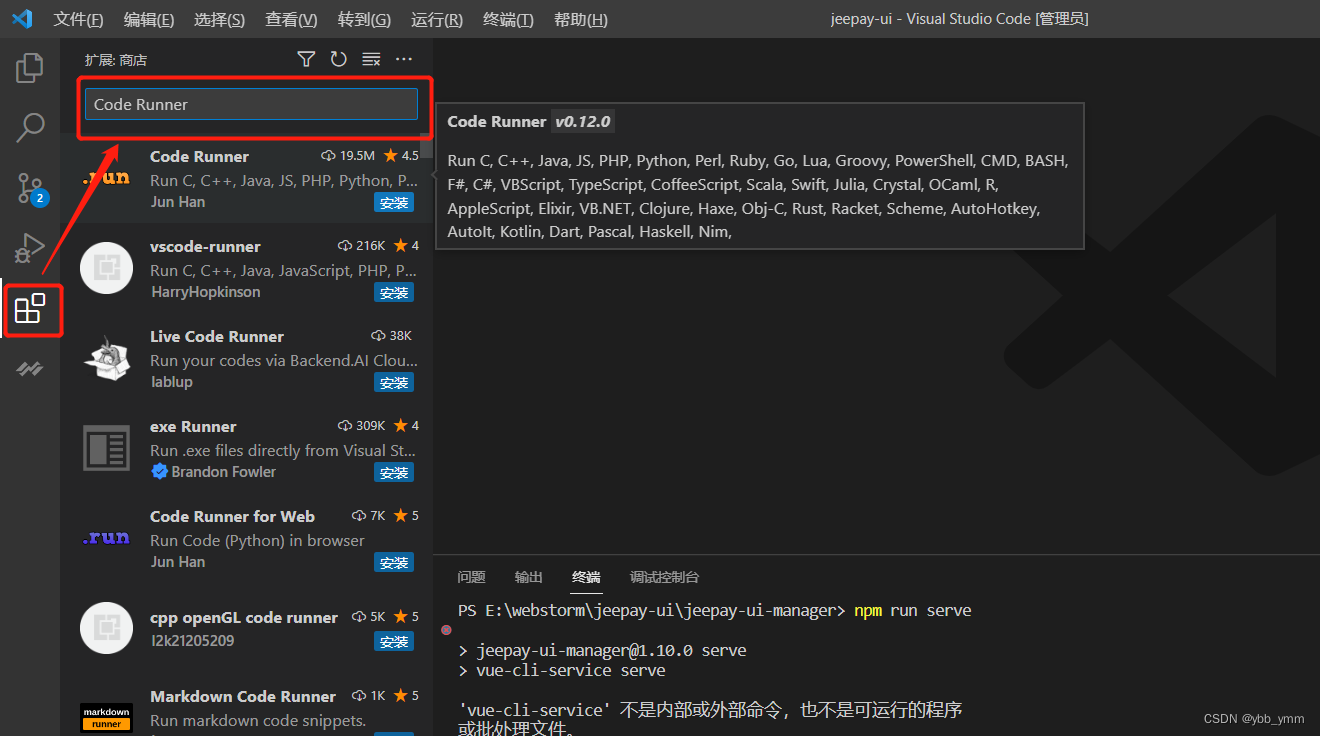
在vscode的扩展中安装三个插件,分别如下:
Code Runner
为静态和动态页面启动具有实时重新加载功能的开发本地服务器
JavaScript(ES6) code snippet
ES6语法中JavaScript的代码片段
Live Server
为静态和动态页面启动具有实时重新加载功能的开发本地服务器
2、创建配置文件
首先打开代码文件夹,先打开文件中的login.js,随便的写上几句,然后运行测试代码。点击左边侧边栏的调试工具,选择创建launch.json文件,选择node.js调试环境。
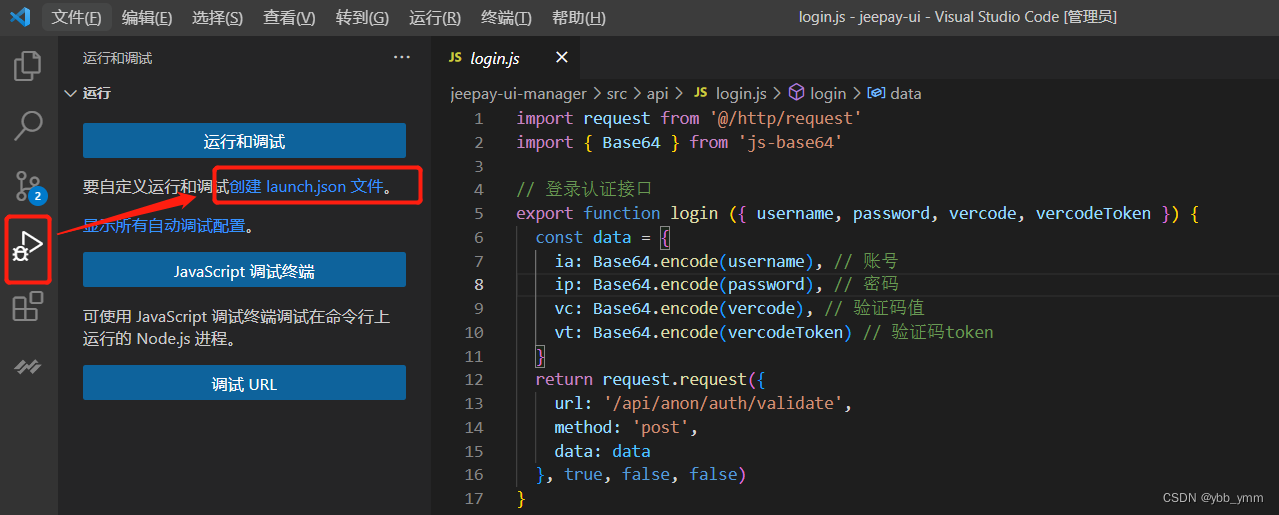
3、调整配置文件内容
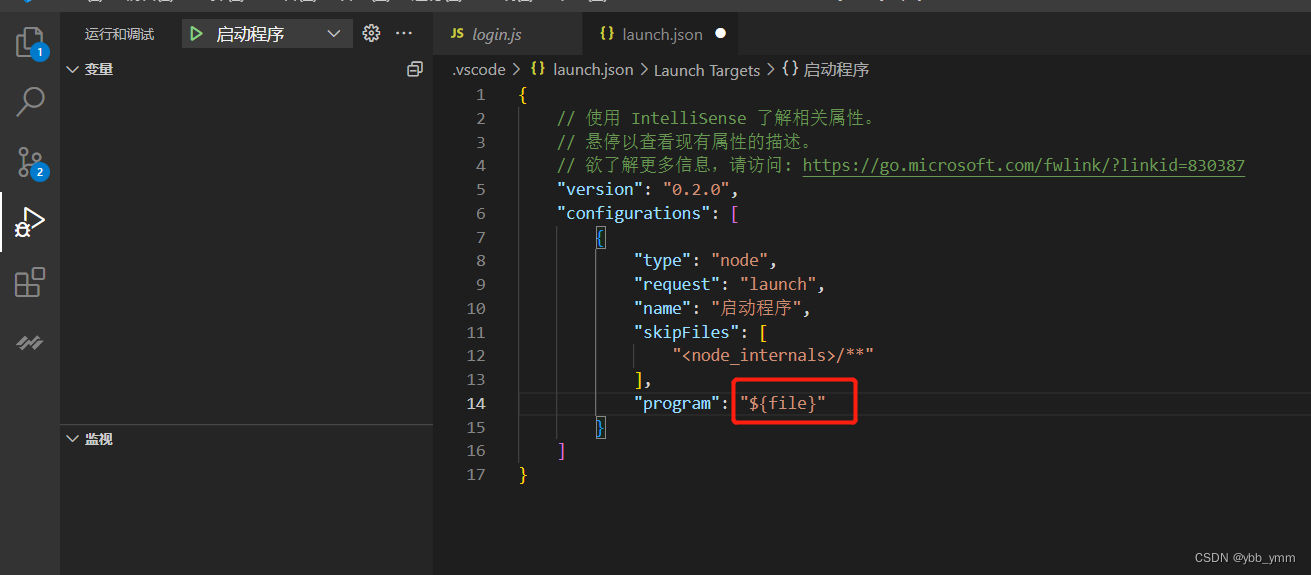
此时配置文件会自动生成,注意将program属性内容修改为${file},这样可以识别当前调试的文件。然后就可以运行文件。
欢迎大家点击下方卡片关注《coder练习生》