【活动回顾】Databend 数据库表达式框架设计与实现 @GOTC

5月28日，“全球开源技术峰会 GOTC 2023 ”圆满落幕。在本次会上，Databend 数据库的 优化器 研发工程师 骆迪安作为嘉宾中的一员，在 rust 专题专区分会场进行了一次主题为《 Rust 实现的先进 SQL Parser 与高效表达式执行框架 — Databend 数据库表达式框架设计与实现》的演讲。

演讲嘉宾： 骆迪安 andylokandy (Andy Lok) · GitHub

嘉宾介绍： 现任 Databend 数据库的优化器研发工程师，主要负责 Databend 计算引擎的 SQL Parser、优化器、类型系统以及向量化执行框架的开发；之前在一家使用 Rust 开发的分布式数据库公司担任分布式事务的研发工程师。从 2015 年开始接触 Rust 这门语言。曾积极参与社区讨论并贡献了几个库，现如今这些库的下载量已经超过了百万。

以下为本次演讲的精彩内容：

Intro

编程语言一直是我非常感兴趣的领域。在业余时间，我会为一门名为 Idris 的语言编译器贡献代码。Idris 的语法与 Haskell 相似，但增加了依赖类型和线性类型等特性。它是一门非常有趣的实验性编程语言。这些年来，我看到 Rust 逐渐将 Idris 的实验特性引入 Rust 生态，例如 effect（也称作关键字泛型）以及最近刚刚稳定的 const generic 特性。在编译器和数据库开发的过程中，我发现它们之间存在许多共通之处，如文本解析成语法树、语法树的语义分析和类型检查等。因此，Databend 中包含了许多借鉴现代编译器实践的精髓。

首先，简要介绍一下 Databend。Databend 是一个全新的云原生数仓，具有即时扩缩容能力，能在数分钟内增加数百倍的算力。得益于 Databend 的存算分离架构以及无状态计算节点设计，扩缩容速度得到了极大的提升。而数据完全托管在对象存储中，确保了云服务在高性价比的同时，实现高可用性。

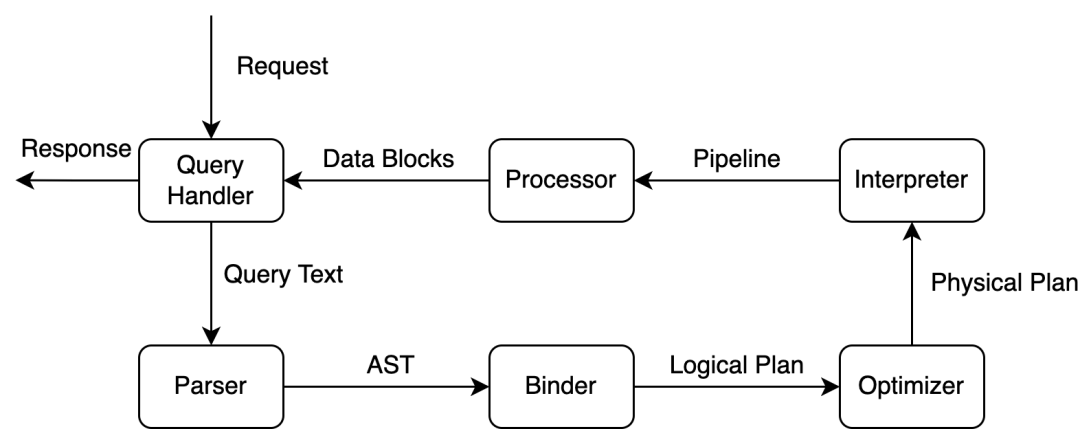
从架构图中可以看到，Databend 由两个独立的组件组成。顶部是元数据存储，相当于集群的目录；第二部分是计算节点，负责从 SQL 解析和优化到数据处理的整个过程。所消耗大量 CPU 的部分主要集中在计算节点。它们通过弹性的存储接口从底部的对象存储中拉取数据。今天的分享重点在计算节点，我将带领大家深入了解 Databend 内部如何将一个 SQL 字符串转化为可执行的中间计划，并计算出结果。

[String] -- [Tokoenize] -- [Parse] -- [Name Resoluation] -- [Type Check] -- [Optimize] -- [Execution]

SQL Parser

在我们详细探讨 Databend 中的 SQL 语法解析器之前，让我们先了解一下语法解析器的基本概念。用户请求的 SQL 字符串会输入语法解析器，语法解析器检查 SQL 中是否包含语法错误，如果语法正确就输出抽象语法树（AST）便于机器理解和处理：

select a + 1 from t

SelectStatement {
    projection: Expr::BinaryOp {
        op: Op::Plus,
        args: [
            Expr::ColumnRef("a"),
            Expr::Constant(Scalar::Int(1))
        ]
    }
    from: "t",
}

解析器过程可以分成两个阶段：Tokenize（分词）阶段和 Parsing（解析）阶段。

首先是 Tokenize 阶段。在这个阶段，我们将 SQL 语句作为输入字符串，任务是将这段字符串切分成具有独立语义的单元，称为 Token。这一步的关键在于利用正则表达式从字符串中识别相邻的有意义的部分，例如关键字、变量名、常量和操作符。

Ident = [_a-zA-Z][_$a-zA-Z0-9]*
Number = [0-9]+
Plus = +
SELECT = SELECT
FROM = FROM

我们从上到下按顺序尝试匹配正则表达式，并重复这个步骤就得到了 Token 序列，这就是 Tokenizer 的基本工作原理。

select a + 1 from t

[
    Keyword(SELECT),
    Ident(a),
    BinOp(+),
    Number(1),
    Keyword(FROM),
    Ident(t),
]

接下来是 Parsing 阶段。通常我们会使用 BNF 来定义 SQL 的语法规则，它描述了有意义的 Token 应该如何组合。

<select_statement> ::= SELECT <expr> FROM <ident>
<expr> ::= <number>
         | <ident>
         | <expr> <op> <expr>
<op> ::= + | - | * | /

在这个阶段，我们将 Token 序列作为输入，然后生成 AST。

SelectStatement {
    projection: Expr::BinaryOp {
        op: Op::Plus,
        args: [
            Expr::ColumnRef("a"),
            Expr::Constant(Scalar::Int(1))
        ]
    }
    from: "t",
}

Choosing an SQL Parser

刚开始，Databend 尝试 fork 了 sqlparser-rs，但后来我们决定放弃这个选择。尽管 sqlparser-rs 已经被诸如 materialize 和 risingwave 这样的 Rust 编写的数据库广泛使用，但其主要问题在于它主要采用手写状态机的方式实现，这使得它在扩展性和容错性上都存在问题。所以，我们意识到需要寻找一种综合性更强、可扩展性更高的解析器方案。

这时，我们选择 nom 作为解析器库，并实现了递归下降 SQL 解析器。nom 是一个受到广泛好评的解析器组合库，它具有高性能和高扩展性，与此同时，它还能为开发者提供更贴近原生的开发体验。与 ANTLR4 和 LALRPOP 等语法生成器相比，nom 作为原生 Rust 开发，能够与其他 Rust 编写的组件完美融合，桥接起来毫不费力。这意味着我们可以充分享受 Rust IDE 的强大支持以及静态类型检查的优势。

当然，nom 也有自己的一些缺点，比如它构建语法规则的过程相对繁琐。为了解决这个问题，我们使用了 nom-rule!() 过程宏。这使得我们可以使用 BNF 来定义语法规则，并能自动生成 nom 解析器，简洁明了。这样一来，我们既保留了 nom 的高性能和高扩展性，又解决了它在语法描述上的问题，提高了可维护性。

Tokenizer

在选择 Tokenizer 方案时，我们选择了社区的 Logos 库。

为了有效地表达 Token 的类型，我们定义一个名为 TokenKind 的 enum 枚举类型。每个 TokenKind 对应一种特定的 Token，例如：关键字、变量名、常量和操作符。每个 TokenKind 都会有一个单独的正则表达式进行匹配，以确保准确地从输入字符串中提取 Token。

然后我们引入了社区的 Logos 库，它会将所有 TokenKind 的正则表达式聚合，并将它们编译成一个高效的状态机和跳表来达到超过任何手写 Tokenizer 的极快的分词性能。

#[allow(non_camel_case_types)]
#[derive(Logos)]
pub enum TokenKind {
    #[regex(r"[ \t\r\n\f]+", logos::skip)]
    Whitespace,

    #[regex(r#"[_a-zA-Z][_$a-zA-Z0-9]*"#)]
    Ident,
    #[regex(r"[0-9]+")]
    Number,

    #[token("+")]
    Plus,

    #[token("SELECT", ignore(ascii_case))]
    SELECT,
    #[token("FROM", ignore(ascii_case))]
    FROM,
}

[
    Token { kind: TokenKind::Select, text: "SELECT", span: 0..6 },
    Token { kind: TokenKind::Ident, text: "a", span: 7..8 },
    Token { kind: TokenKind::Plus, text: "+", span: 9..10 },
    Token { kind: TokenKind::Number, text: "1", span: 11..12 },
    Token { kind: TokenKind::From, text: "from", span: 13..17 },
    Token { kind: TokenKind::Ident, text: "t", span: 18..19 },
]

除了 TokenKind 的定义，Token 本身还包括了一个重要的属性——span。span 记录了 Token 在原始字符串中的起始和结束位置。这在后续阶段很有用，比如当我们需要针对 SQL 语句中的特定部分向用户报告错误时，可以利用 span 属性精确定位到具体的位置。

error: 
  --> SQL:1:19
  |
1 | create table a (c varch)
  | ------          - ^^^^^ expected `BOOLEAN`, `BOOL`, `UINT8`, `TINYINT`, `UINT16`, `SMALLINT`, or 33 more ...
  | |               |  
  | |               while parsing `<column name> <type> [DEFAULT <default value>] [COMMENT '<comment>']`
  | while parsing `CREATE TABLE [IF NOT EXISTS] [<database>.]<table> [<source>] [<table_options>]`

Parser

接下来, 让我们介绍一下如何在 Databend 中使用 nom 来实现递归下降 SQL 解析器。

递归下降解析器主要由两种 parser 组成：

Terminal parser：这是最基本的解析器，用于匹配特定 TokenKind 的 Token。在 Databend 的 SQL parser 中，我们定义了 match_token() 和 match_text() 两个 Terminal parser。

fn match_text(text: &str) -> impl FnMut(&[Token]) -> IResult<&[Token], Token> {
    satisfy(|token: &Token| token.text == text)(i)
}

fn match_token(kind: TokenKind) -> impl FnMut(&[Token]) -> IResult<&[Token], Token> {
    satisfy(|token: &Token| token.kind == kind)(i)
}

2. Combinator parser：允许将多个小的解析器组合成较大的解析器。这是我们构建复杂逻辑的基础。以下是一些常见的组合器：

*   tuple(a, b, c)：会让多个 parser 按顺序排列（例如先是 a，然后是 b，接着是 c）。它们需要按照预期的顺序逐个成功才算作最后的成功。
*   alt(a, b, c)：尝试多个 parser 分支（例如 a，b 或 c），直到满足第一个成功条件。如果全部失败，解析器将报告错误。
*   many0(a)：贪婪地循环调用相同的 parser。如果无法继续，这个解析器将成功返回已匹配的 Token 序列。可能为空。
*   many1(a)：贪婪地循环调用相同的 parser，但至少需要匹配成功一次。如果至少匹配成功一次，解析器会返回 Token 序列。
*   opt(a)：允许 parser 失败。当 parser 失败时，将返回 `None`。成功时将返回成功匹配的结果。

我们来看一个实际的例子，我们知道 select_statment 的 BNF 是：

<select_statement> ::= SELECT <expr>+ FROM <ident>

我们使用 nom 提供的组合子来组装相应的语法树：

tuple((
    match_token(SELECT),
    many1(expr),
    match_token(FROM),
    match_token(Ident),
))

在这里关键字使用 match_token 识别；循环多个的 <expr>+ 用 many1 来实现。nom 的语法树会帮助我们把一维的 Token 序列识别成立体的 Parse Tree。

SELECT a + 1 FROM t

("SELECT", (+ a 1), FROM, t)

到这里 nom 仅仅帮助我们构建了一课符合语法结构的 Parse Tree，它的节点都是由 Token 组成的，所以这个还不是我们需要的 AST，所以进一步地，我们用 map 把 Token 树，于是最终我们得到了 AST:

use nom::combinator::*;
use nom::multi::*;

fn select_statement(input: &[Token]) -> IResult<&[Token], SelectStatement> {
    map(
        tuple((
            match_token(SELECT),
            many1(expr),
            match_token(FROM),
            match_token(Ident),
        )),
        |(_, projections, _, from)| SelectStatement {
            projections,
            from,
        }
    )(input)
}

nom-rule

nom 使用原生 Rust 函数构造语法树，显得过于冗余和不清晰。我们希望可以使用类似 BNF 的形式来描述 SQL 这种复杂的语法结构，所以我们使用了 nom-rule 过程宏来做到这一点。它输入类似 BNF 的语法定义，然后转换成 nom 的组合子函数。因为 nom-rule 生成的是合法的 Rust 代码，所以我们可以把 nom-rule 直接嵌入到 nom 代码的任何位置。

fn select_statement(input: &[Token]) -> IResult<&[Token], SelectStatement> {
    map(
        nom_rule! { 
            SELECT ~ #expr+ ~ FROM ~ #ident 
        },
        |(_, projections, _, from)| SelectStatement {
            projections,
            from,
        }
    )(input)
}

常用的几个语法结构有这些，它们分别和 nom 的组合子一一对应：

Rule	Translated
TOKEN	match_token(TOKEN)
"+"	match_text("+")
a ~ b ~ c	tuple((a, b, c))
(...)*	many0(...)
(...)+	many1(...)
(...)?	opt(...)
a	b	c	alt((a, b, c))

Left Recursion

现在我们来探讨一个实际中实现解析器会遇到的问题 - 左递归问题。

假设我们打算定义算术表达式的语法规则，比如说解析一个简单的算术表达式：1 + 2，理想情况下，我们期望将这个表达式解析成一个树状结构，其中操作符 "+" 作为树的根节点，"1" 和 "2" 分别作为左子节点和右子节点。根据直觉我们会定义成：

<expr> ::= <number>
         | <expr> + <expr>

然而，实际上这样的解析器会报告错误，这是因为 1 + 2 中的 1 会首先被识别为，剩下的 + 2 并不能匹配任何一条规则。

所以我们必须把更整体的分支放到前面，然后定义会变成：

<expr> ::= <expr> + <expr>
         | <number>

然而，实际上这样做会让解析器陷入死循环。因为调用解析器之后它做的第一件事情是再次调用自己，没有任何退出递归的机会。

我们使用 Pratt 算法来解决这个问题。Pratt 算法是在 1973 年提出的一种简易算法。它专门用于处理一元和二元操作符。输入表达式元素的一维序列，即 [1, +, 2]，以及定义 +, -, *, / 为二元中置操作符，然后采用 Pratt 算法处理这些表达式元素，组装成树状结构。具体算法由于时间关系在这里不作展开了。

Type Check

SQL 字符串经过 Parser 变成了 AST，Parser 输出的 AST 一定符合语法规则，但不一定有意义，例如 1 + 'foo' 这个表达式，它遵守语法规则，但仍然是无意义的。因此，在解析得到 AST 后，我们会紧接着对表达式的类型进行检查。一旦类型检查通过，我们就可以保证表达式具有明确的运行时语义。

在 Databend 中，类型信息主要依赖于函数签名。我们来看一个表达式的例子：

1 + 'foo'

首先，Typechecker 对其进行简化，将其转换为函数调用：

plus(1, 'foo')

然后，类型检查器可以轻松推断出：

1 :: Int8
'foo' :: String

此外，由于 plus 函数提供了一些重载方法：

plus(Int8, Int8) -> Int8
plus(Int16, Int16) -> Int16
plus(Timestamp, Timestamp) -> Timestamp
plus(Date, Date) -> Date

我们可以轻松地发现，plus(Int8, String) 并不符合任何重载方法。因此，类型检查器可以报错，指出：

1 + 'foo'
  ^ function `plus` has no overload for parameters `(Int8, String)`

  available overloads:
    plus(Int8, Int8) -> Int8
    plus(Int16, Int16) -> Int16
    plus(Timestamp, Timestamp) -> Timestamp
    plus(Date, Date) -> Date

Type Judgement

Type Checking 的概念源于类型理论。在类型理论中，我们使用专门的记号来定义类型推导规则。例如，我们在以下示例中运用了这些推导规则：

⊢ TRUE : Boolean

符号 ⊢ 读作 "推导出"。这条规则表示字面量 TRUE 的类型为布尔类型。

同样地，我们也为整数和字符串字面量定义了类型：

⊢ 1 : Int8
⊢ "foo" : String

接下来，我们为 plus() 函数定义推导规则：

Γ⊢ e1 : Int8  Γ⊢ e2 : Int8
----------------------
 Γ⊢ plus(e1, e2) : Int8

分号上方部分是推导的前提条件，若分号上的所有条件都满足，分号下的规则便成立。这表明如果在当前类型环境（Type Environment）中，表达式 e1 与 e2 的类型皆为 Int8，那么我们可推导出 plus(e1, e2) 的类型为 Int8。

表达式可以包含自由变量（free variables），在 SQL 中，数据列就是自由变量。例如，在查询 SELECT 1 + a 中的 a 就是一个自由变量。当检查表达式 1 + a 时，我们无法确定变量 a 的类型；若 a 是表的数据列，我们需要从表元数据中查询 a 的类型。

若 a 是子查询的结果列，则需要先检查子查询以得到 a 的类型：

SELECT 1 + a from (SELECT number as a from numbers(100))

在上下文中，变量名称与类型具有映射关系。这种信息称为类型环境（Type Environment），用 Γ 符号表示。类型环境可以有多种来源，但在 Typechecker 中，我们将其抽象为一个外部界面。我们只需了解，每个变量都可以从类型环境中查询到一个确定的类型。

Subtype

Databend 引入了子类型概念，数据类型可以根据需要适当自动回退到一个更小约束的类型。比如 1 + 256 的入参类型是 plus(Int8, Int16)，根据 plus() 函数重载列表

plus(Int8, Int8) -> Int8
plus(Int16, Int16) -> Int16
...

我们发现没有一个重载可完全符合入参类型。但我们知道 Int8 可以无损地由 Int16 类型表示，也就是说 Int8 是 Int16 的 subtype

Int8 <: Int16

为此我们稍微修改一下函数类型规则：

Γ⊢ e1 : T1   Γ⊢ e2 : T2   T1 <: Int16   T2 <: Int16
---------------------------------------------------
             Γ⊢ plus(e1, e2) : Int16

这样可以推导出 1 + 256 的类型是 Int16。

在实际实践中，我们会在必要进行子类型转换的地方插入 CAST，所以 1 + 256 会变成 CAST(1 AS INT16) + 256。

Generic

在 Databend 中，我们支持数组类型，例如：

⊢ [1, 2, 3] : Array<Int8>

当我们尝试为数组定义函数时，会发现无法列举出所有重载。以 get() 函数为例，该函数用于根据下标从数组中提取一个元素，因此函数的返回类型取决于数组的元素类型。如下所示：

get(Array<Int8>, Int64) -> Int8
get(Array<Array<Int8>>, Int64) -> Array<Int8>
get(Array<Array<Array<Int8>>>, Int64) -> Array<Array<Int8>>
...

为了解决这个问题，我们在 Typechecker 中引入了泛型。借助泛型，可以用一个简单的重载定义 get() 函数：

get<T>(Array<T>, Int64) -> T

当尝试检查表达式 get(Array<Int8>, Int64) 时，Typechecker 会通过比较签名类型 Array<T> 和实际参数类型 Array<Int8> 来解析替换关系 T=Int8。因此，将签名中返回值类型的 T 替换为 Int8，就可以得到函数类型 Int8。这个解析替换关系的算法被称为 Unification 算法，它非常有趣，但由于时间原因在此不展开讲解。如果您感兴趣，强烈推荐去了解这个算法。

Vectorized Evaluation

为了在内存中存储数据，我们定义了一些数据结构：

enum Value {
    Scalar(Scalar),
    Column(Column),
}

enum Scalar {
    Int8(i8),
    Int16(i16),
    Boolean(bool),
    ...
}

enum Column {
    Int8(Vec<i8>),
    Int16(Vec<i16>),
    Boolean(Vec<bool>),
    ...
}

表达式 1 + a 通过类型检查后得到 Expr 结构：

Expr::FunctionCall {
    name: "plus",
    args: [
        Expr::Constant(Scalar::Int8(1)),
        Expr::ColumnRef("a"),
    ],
    eval: Box<Fn([Value]) -> Value>,
}

FunctionCall 包含一个名为 eval 的闭包。这个闭包在类型检查阶段被确定，并负责实际的数据计算。由于 Databend 实现了向量化计算，eval 会一次接收一批数据作为参数，并批量计算并输出相同行数的结果。特殊情况下，如果输入的每一行都相同，我们使用 Value::Scalar 进行存储。

以 plus(Int8, Int8) 为例，其定义类似于：

registry.register_function(Function {
    signature: FunctionSignature {
        name: "plus",
        arg: [DataType::Int8, DataType::Int8],
        return_type: DataType::Int8,
    },
    eval: |lhs: Value, rhs: Value| -> Value {
        match (lhs, rhs) {
            (Value::Scalar(Scalar::Int8(lhs)), Value::Scalar(Scalar::Int8(rhs))) => {
                Value::Scalar(Scalar::Int8(lhs + rhs))
            },
            (Value::Column(Column::Int8(lhs)), Value::Scalar(Scalar::Int8(rhs))) => {
                let result: Vec<i8> = lhs.iter().map(|lhs| *lhs + rhs).collect();
                Value::Column(Column::Int8(result))
            },
            (Value::Scalar(Scalar::Int8(lhs)), Value::Column(Column::Int8(rhs))) => {
                let result: Vec<i8> = rhs.iter().map(|rhs| lhs + *rhs).collect();
                Value::Column(Column::Int8(result))
            },
            (Value::Column(Column::Int8(lhs)), Value::Column(Column::Int8(rhs))) => {
                let result: Vec<i8> = lhs.iter().zip(rhs.iter()).map(|(lhs, rhs)| *lhs + *rhs).collect();
                Value::Column(Column::Int8(result))
            },
            _ => unreachable!()
        }
    }
})

在这里我们看到相同的加法逻辑出现了 4 次，这是因为我们需要分别处理 Value::Scalar 或 Value::Column 的左右输入参数情况。因此，我们可以将这个模式抽象出来：

impl FunctionRegistry {
    fn register_2_arg_int8(&mut self, name: String, eval: impl Fn(i8, i8) -> i8) {
        self.register_function(Function {
            signature: FunctionSignature {
                name: "plus",
                arg: [DataType::Int8, DataType::Int8],
                return_type: DataType::Int8,
            },
            eval: |lhs: Value, rhs: Value| -> Value {
                match (lhs, rhs) {
                    (Value::Scalar(Scalar::Int8(lhs)), Value::Scalar(Scalar::Int8(rhs))) => {
                        Value::Scalar(Scalar::Int8(eval(lhs, rhs)))
                    },
                    (Value::Column(Column::Int8(lhs)), Value::Scalar(Scalar::Int8(rhs))) => {
                        let result: Vec<i8> = lhs.iter().map(eval(*lhs, rhs)).collect();
                        Value::Column(Column::Int8(result))
                    },
                    (Value::Scalar(Scalar::Int8(lhs)), Value::Column(Column::Int8(rhs))) => {
                        let result: Vec<i8> = rhs.iter().map(eval(lhs, *rhs)).collect();
                        Value::Column(Column::Int8(result))
                    },
                    (Value::Column(Column::Int8(lhs)), Value::Column(Column::Int8(rhs))) => {
                        let result: Vec<i8> = lhs.iter().zip(rhs.iter()).map(|(lhs, rhs)| eval(*lhs, *rhs)).collect();
                        Value::Column(Column::Int8(result))
                    },
                    _ => unreachable!()
                }
            }
        });
    }
}

这样我们可以更方便地注册 Int8 类型的算术函数：

registry.register_2_arg_int8("plus", |lhs: i8, rhs: i8| lhs + rhs);
registry.register_2_arg_int8("minus", |lhs: i8, rhs: i8| lhs - rhs);

这个模式中我们抽象出了处理 Value 的分类讨论，但仍需要针对每种输入参数类型进行一次实现。因此，我们继续将输入参数类型抽象出来。从这一步开始，抽象变得更加复杂。因为闭包的输入参数类型在 Rust 编译期已经确定下来，这就意味着无法使用单个 |lhs, rhs| lhs + rhs 来同时定义 plus(Int8, Int8) -> Int8 和 plus(Int16, Int16) -> Int16两种重载。因此，在这里我们需要求助于一些 Rust 的高级技巧：

首先，为 Int8 数据类型定义一个空结构体：

struct Int8Type;

然后，将处理 Int8 类型数据的操作放入 Int8Type 中：

trait ValueType {
    type Scalar;

    fn data_type() -> DataType;
    fn downcast_scalar(Scalar) -> Self::Scalar;
    fn upcast_scalar(Self::Scalar) -> Scalar;
    fn iter_column(Column) -> impl Iterator<Item = Self::Scalar>;
    fn collect_iter(impl Iterator<Item = Self::Scalar>) -> Column;
}

impl ValueType for Int8Type {
    type Scalar = i8;

    fn data_type() -> DataType {
        DataType::Int8
    }
    fn downcast_scalar(scalar: Scalar) -> Self::Scalar {
        match scalar {
            Scalar::Int8(val) => val,
            _ => unreachable!(),
        }
    }
    fn upcast_scalar(scalar: Self::Scalar) -> Scalar {
        Scalar::Int8(scalar)
    }
    fn iter_column(col: Column) -> impl Iterator<Item = Self::Scalar> {
        match col {
            Column::Int8(col) => col.iter().cloned(),
            _ => unreachable!(),
        }
    }
    fn collect_iter(iter: impl Iterator<Item = Self::Scalar>) -> Column {
        let col = iter.collect();
        Column::Int8(col)
    }
}

在定义了必要操作之后，我们可以对 register_2_arg_int8 进行修改。我们将输入参数类型从固定的 i8 更改为灵活的三个泛型 I1，I2 和 Output，分别表示第一个参数类型、第二个参数类型和输出类型：

impl FunctionRegistry {
    fn register_2_arg<I1: ValueType, I2: ValueType, Output: ValueType>(&mut self, name: String, eval: impl Fn(I1::Scalar, I2::Scalar) -> Output::Scalar) {
        self.register_function(Function {
            signature: FunctionSignature {
                name: "plus",
                arg: [I1::data_type(), I2::data_type()],
                return_type: Output::data_type(),
            },
            eval: |lhs: Value, rhs: Value| -> Value {
                match (lhs, rhs) {
                    (Value::Scalar(lhs), Value::Scalar(rhs)) => {
                        let lhs: I1::Scalar = I1::downcast_scalar(lhs);
                        let rhs: I2::Scalar = I2::downcast_scalar(rhs);
                        let res: Output::Scalar = eval(lhs, rhs);
                        Output::upcast_scalar(O::upcast_scalar(res))
                    },
                    ...
                }
            }
        });
    }
}

现在，我们已经借助 Rust 泛型系统将类型信息抽象化：

registry.register_2_arg::<Int8Type, Int8Type, Int8Type>("plus", |lhs: i8, rhs: i8| lhs + rhs);
registry.register_2_arg::<Int8Type, Int8Type, Int8Type>("minus", |lhs: i8, rhs: i8| lhs - rhs);

有了这个改进，我们可以非常方便地注册其他类型的重载函数，例如：

registry.register_2_arg::<Int16Type, Int16Type, Int16Type>("plus", |lhs: i16, rhs: i16| lhs + rhs);
registry.register_2_arg::<Int16Type, Int16Type, Int16Type>("minus", |lhs: i16, rhs: i16| lhs - rhs);

Golang

说来也巧，之前我也参与过一个使用 golang 编写的数据库项目。一般为了避免引战，我不会在公开场合讨论 Rust 和 Golang 的优劣。但是今天是rust专场，所以我就可以说一说了。这是我从 golang 项目中摘取的定义 abs() 函数的片段，它有 135 行，定义了 5 个结构体和 5 个函数，分别是一个函数级专微型类型检查器，4个 struct 用来分别代表不同的函数从在，以及对每个类型重载分别定义一次计算过程，由于 golang 没有能够把向量化循环抽象出来的机制，那么只好在每一个重载内部都手动重写一次for循环。

这里 135 行只定义了一个 abs 函数，定义其他上百个函数的时候都要把重复一遍相同过程。

这样对比下来，rust 在运行效率和可维护性上都是明显更好一些。其实不是想讨论 rust 和 golang 谁更好这种问题。只是说每一种语言都有适合的场景，而在数据库领域，rust 在应对功能复杂性上比 golang 更适合一些。

Conclusion

在本次分享中，我向大家介绍了 Databend 中独特的 SQL 解析器和表达式框架。我们使用了诸如 Rust、nom、Logos、Pratt 算法、类型检查等工具和技术来实现一个高效的、可扩展的解析器和计算框架。这使得我们能够快速迭代 Databend，不断优化我们的数据库系统，同时保持高性能和高可扩展性。

在演讲的最后，我还想向各位观众推荐一本书——《Types and Programing Language》。这本书由 Benjamin C. Pierce 编写，系统地介绍了类型理论、程序语言和编译器相关的知识。通过阅读这本书，您将深入了解类型系统、类型检查、类型推导等概念，这对于研究和开发编译器以及数据库都有很大帮助。

最后，我要感谢这次机会，让我能和大家一起分享 Databend 中的这些技术与实践。谢谢大家！