一、题目
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
二、示例
2.1> 示例 1:
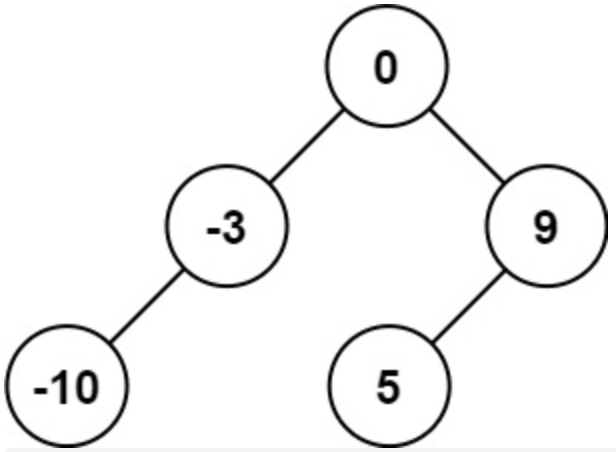
【输入】nums = [-10,-3,0,5,9]
【输出】[0,-3,9,-10,null,5]
【解释】[0,-10,5,null,-3,null,9] 也将被视为正确答案:
2.2> 示例 2:
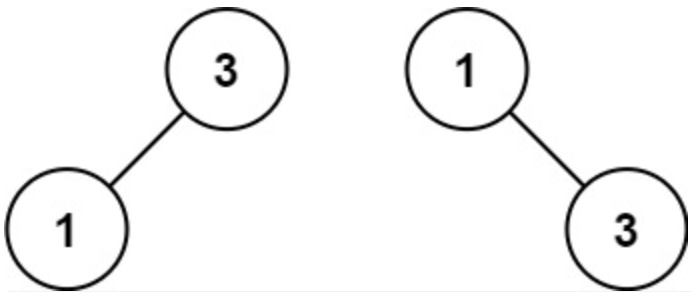
【输入】nums = [1,3]
【输出】[3,1]
【解释】[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1<= nums.length <=10^4-10^4<= nums[i] <=10^4nums按 严格递增 顺序排列
三、解题思路
根据题目要求,我们要根据题目给出的nums数组,将其转换为一棵 高度平衡 二叉搜索树。那么我们就要保障根节点的左子树节点总数与右子树节点总数之差不要超过1。
首先,我们要获得中心节点mid,有如下两种获取方式:
【方式1】通过
数组长度除以2获得中心点mid—— nums.length / 2;
【方式2】通过双指针除以2获得中心点mid—— (start + end) / 2;
然后,我们创建min值对应的TreeNode,即:new TreeNode(nums[mid]); 由于我希望减少数组切割的性能消耗,所以采用双指针的方式进行“数组拆分”操作。那么寻找中心点mid也就自然而然的采用“方式2”了。此时,将原有数组拆分为两部分,分别为[start, mid-1]和[mid+1, end],然后再分别针对这两部分数组再次执行上面操作即可。
通过以上的解题思路,我们在编码时,就可以通过递归调用方式进行解题了。为了便于大家理解,下面我们以输入nums = [-10,-3,0,5,9]为例,看一下具体的解题过程。请见下图所示:
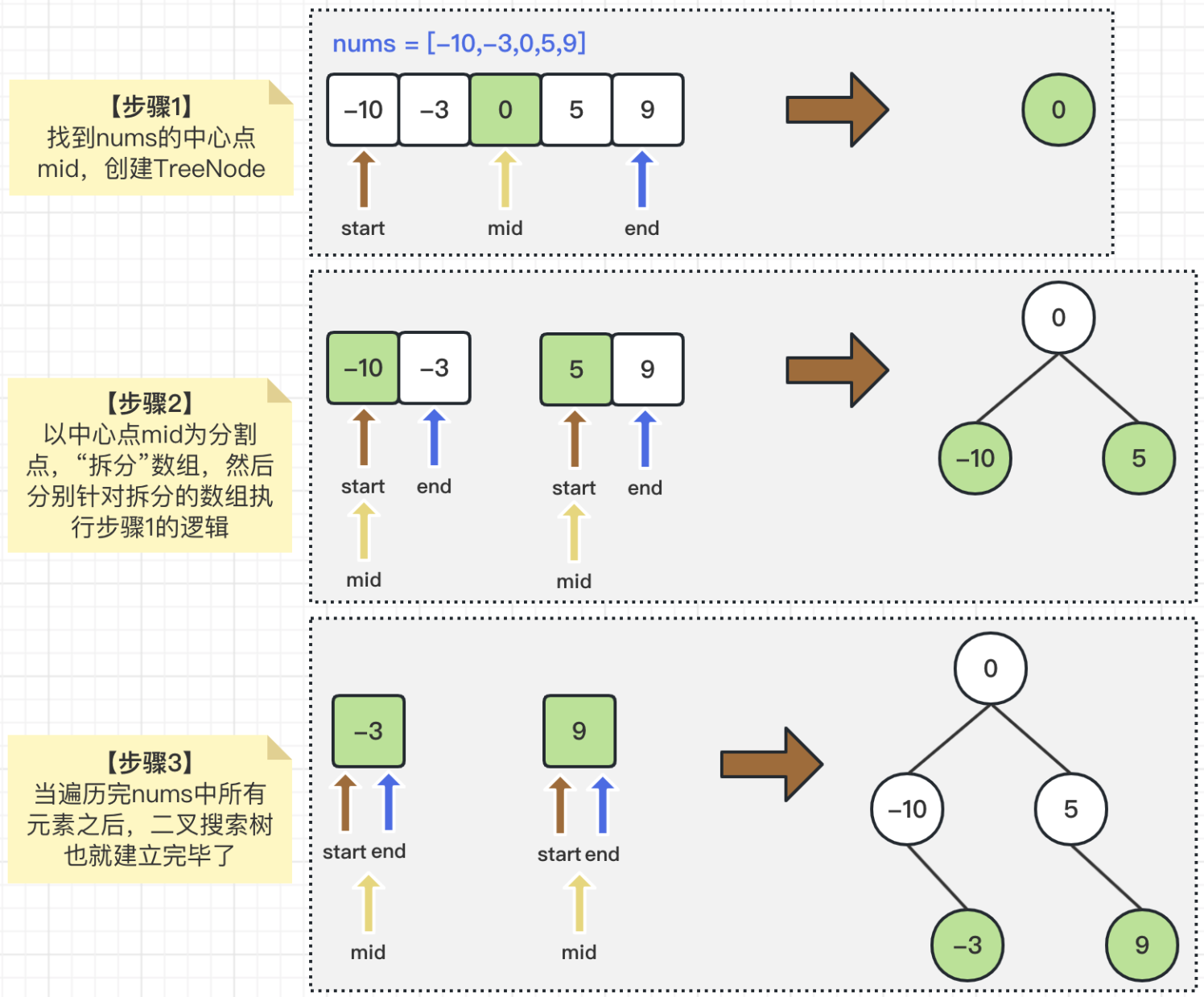
四、代码实现
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return sort(nums, 0, nums.length - 1);
}
public TreeNode sort(int[] nums, int start, int end) {
if (start > end) return null;
int mid = (start + end) / 2; // nums数组的寻找中心点
TreeNode node = new TreeNode(nums[mid]);
node.left = sort(nums, start, mid - 1); // 获得node的左节点
node.right = sort(nums, mid + 1, end); // 获得node的右节点
return node;
}
}
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」