完全背包
前情提要: 0-1背包指的是给定背包重量,将物品放入背包中,使得背包中的物品达到最大的价值。(每个物品只能往其中放一次)
在0-1背包问题中,第二层for循环需要是倒序遍历才可以保证每个物品只使用一次,如果物品使用的次数没有限制,只需要将第二个for循环改成正序遍历即可。
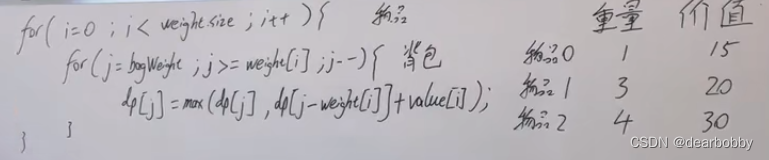
完全背包:
- 第二层for循环需要变成正序
- 完全背包:背包和物品的顺序没有要求,先遍历背包或者先遍历物品都可以,都可以得到背包中的最大价值。
# 代码来自于代码随想录
# 先遍历物品,再遍历背包
def test_complete_pack1():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
dp = [0]*(bag_weight + 1)
for i in range(len(weight)):
for j in range(weight[i], bag_weight + 1):
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bag_weight])
# 先遍历背包,再遍历物品
def test_complete_pack2():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
dp = [0]*(bag_weight + 1)
for j in range(bag_weight + 1):
for i in range(len(weight)):
if j >= weight[i]: dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bag_weight])
if __name__ == '__main__':
test_complete_pack1()
test_complete_pack2()
518. 零钱兑换 II
完全背包问题: 装满这么大的背包有多少中可能,零钱可以想象成物品,物品有无限次的存取机会。
- dp[j]:背包容量为j,有多少种可能性
- 递推公式(类似于装满一个背包有多少种方法):dp[j] += dp[j-nums[i]],后放入一个物品取决于之前的物品情况,因而需要将该式子抽象成求和的问题。
- dp数组的初始化:
- 遍历顺序
- 打印dp数组
注意:
- 先遍历背包再遍历物品是排列数
- 先遍历物品再遍历背包是组合数
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
# 可以抽象成背包问题,每个物品可以使用无限次,因此这是一个完全背包的问题。
# 也可以使用回溯法进行求解
nums = coins
target = amount
dp = [0] * (target + 1)
dp[0] = 1
# 先物品,后背包(排列)
for i in range(len(nums)):
for j in range(nums[i],target+1):
dp[j] += dp[j-nums[i]]
return dp[target]
377. 组合总和 Ⅳ
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
if min(nums) > target:
return 0
dp = [0] * (target + 1)
dp[0] = 1
'''
# 先物品,后背包(排列)
for i in range(len(nums)):
for j in range(nums[i],target+1):
dp[j] += dp[j-nums[i]]
print(nums[i],j,dp)
return dp[target]
'''
# 先物品,后背包(组合)
for j in range(target+1):
for i in range(len(nums)):
if j-nums[i]>=0:
dp[j] += dp[j-nums[i]]
return dp[target]
拓展:为什么顺序不同解决的排列和组合的问题也不同(以组合综合问题为例分析)
分析: 边将通过dp数组的输出结果来分析为什么背包和物品的遍历顺序不同,对应的排列和组合的问题也不同。
先背包后物品: 组合问题(组合总和)[1,2]&[2,1]算作两种情况
for j in range(target+1):
for i in range(len(nums)):
if j-nums[i]>=0:
dp[j] += dp[j-nums[i]]
print(j,nums[i],dp)
return dp[target]


如果先遍历背包重量的话,那么过程中每次都会重新遍历一次物品,例如遍历背包重量为3,此时的前面的状态
背包重量为2:(1,1)(2)
背包重量为1:(1)
背包重量为0:(0)
先遍历重量为1的物品,得到如下结果(1,1,1)(2,1)
遍历重量为2的物品,得到如下结果(1,2)
遍历重量为3的物品,得到如下结果(3)
此时一共有4中情况,将前面的情况全都囊括再其中了,如果按照此种方式求解的话,得到的结果是组合的情况。
先物品后背包: 排列问题(零钱兑换)[1,2]&[2,1]算作一种情况
for i in range(len(nums)):
for j in range(nums[i],target+1):
dp[j] += dp[j-nums[i]]
print(j,nums[i],dp)
return dp[target]